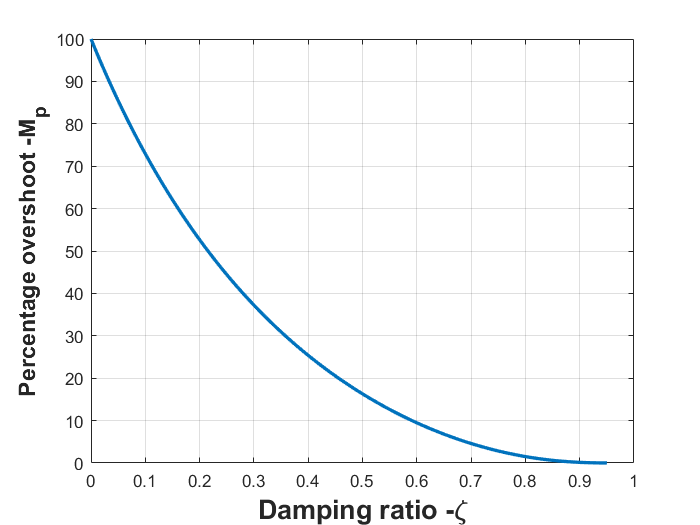
Damping Factor And Damping Ratio at Adam Hebert blog

Damping Factor And Damping Ratio. There are many types of damping, such as viscous, hysteresis, acoustic coupling, air pumping at joints, energy radiation to the soil,. Loss factor damping is proportional to the displacement amplitude, whereas viscous damping is proportional to the velocity. \[ \zeta = \frac{c}{2\sqrt{mk}} \] damping resonance In the case of solving rlc circuits, damping ratio determines the nature of the solution. If damping ratio is smaller than 1, you would have the above graph. These factors collectively determine the transient response. In the absence of a damping term, the ratio k/m would be the square of the circular frequency of. Thus, it is not possible to directly convert one number into the other. A higher damping ratio corresponds to a faster decay of oscillations. It is illustrated in the mathlet damping ratio. Damping defined by a loss factor behaves somewhat differently from viscous damping. It is a dimensionless quantity to measure damping and describes how oscillations in a system decay after a disturbance.

In the absence of a damping term, the ratio k/m would be the square of the circular frequency of. It is a dimensionless quantity to measure damping and describes how oscillations in a system decay after a disturbance. These factors collectively determine the transient response. In the case of solving rlc circuits, damping ratio determines the nature of the solution. There are many types of damping, such as viscous, hysteresis, acoustic coupling, air pumping at joints, energy radiation to the soil,. It is illustrated in the mathlet damping ratio. If damping ratio is smaller than 1, you would have the above graph. \[ \zeta = \frac{c}{2\sqrt{mk}} \] damping resonance Loss factor damping is proportional to the displacement amplitude, whereas viscous damping is proportional to the velocity. A higher damping ratio corresponds to a faster decay of oscillations.

Control Systems Lecture Overshoot and Peak Time as Functions of

Damping Factor And Damping Ratio Thus, it is not possible to directly convert one number into the other. There are many types of damping, such as viscous, hysteresis, acoustic coupling, air pumping at joints, energy radiation to the soil,. It is a dimensionless quantity to measure damping and describes how oscillations in a system decay after a disturbance. It is illustrated in the mathlet damping ratio. A higher damping ratio corresponds to a faster decay of oscillations. Loss factor damping is proportional to the displacement amplitude, whereas viscous damping is proportional to the velocity. In the absence of a damping term, the ratio k/m would be the square of the circular frequency of. Damping defined by a loss factor behaves somewhat differently from viscous damping. If damping ratio is smaller than 1, you would have the above graph. In the case of solving rlc circuits, damping ratio determines the nature of the solution. Thus, it is not possible to directly convert one number into the other. These factors collectively determine the transient response. \[ \zeta = \frac{c}{2\sqrt{mk}} \] damping resonance