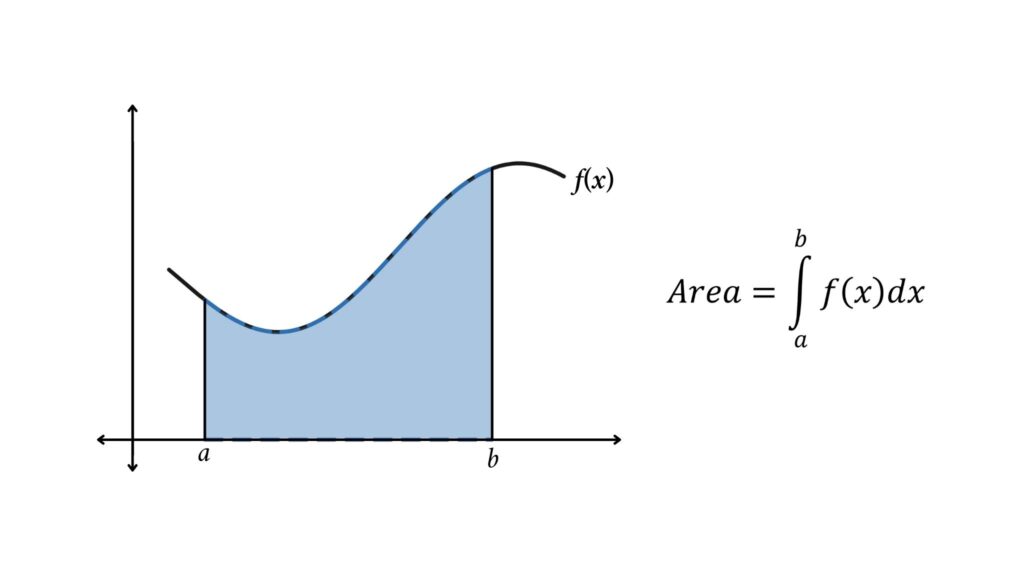
Derivatives Integrals And The Area Under The Curve . Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. To find the area between two curves defined by functions, integrate the difference of the functions. We will now study the area of very irregular figures. 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. How to find the area under a curve using integration. The total area under a curve can be found using this formula. The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. In particular, if we have a. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral.
from educatemath.com
Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. The total area under a curve can be found using this formula. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. We will now study the area of very irregular figures. How to find the area under a curve using integration. In particular, if we have a. Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. To find the area between two curves defined by functions, integrate the difference of the functions. The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand.
Area Under the Curve and Area between the Two Curves
Derivatives Integrals And The Area Under The Curve Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. In particular, if we have a. The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. We will now study the area of very irregular figures. The total area under a curve can be found using this formula. 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. To find the area between two curves defined by functions, integrate the difference of the functions. How to find the area under a curve using integration. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral.
From www.vrogue.co
Integral As The Area Under A Curve Matplotlib 3 1 2 D vrogue.co Derivatives Integrals And The Area Under The Curve Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. How to find the area under a. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
Finding the Area Between Two Curves by Integration YouTube Derivatives Integrals And The Area Under The Curve Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. The total area under a curve can be found using this formula. 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. The fundamental theorem of. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
Finding the Area Under a Curve using Definite Integration YouTube Derivatives Integrals And The Area Under The Curve The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. The total area under a curve can be found using this formula. In particular, if we have a. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. Just as definite. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
Area under and between Curves by Integration ExamSolutions YouTube Derivatives Integrals And The Area Under The Curve 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. The fundamental theorem of calculus, part 1 shows the relationship between the. Derivatives Integrals And The Area Under The Curve.
From www.vrogue.co
Integral As The Area Under A Curve Matplotlib 3 1 2 D vrogue.co Derivatives Integrals And The Area Under The Curve 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and. Derivatives Integrals And The Area Under The Curve.
From www.cuemath.com
Area Under The Curve Method, Formula, Solved Examples, FAQs Derivatives Integrals And The Area Under The Curve The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. We will now study the area of very irregular figures. How to find the area under a curve using integration. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all. Derivatives Integrals And The Area Under The Curve.
From educatemath.com
Area Under the Curve and Area between the Two Curves Derivatives Integrals And The Area Under The Curve We will now study the area of very irregular figures. Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. In particular, if we have a. Intuitively, $\int_a^b. Derivatives Integrals And The Area Under The Curve.
From www.nagwa.com
Question Video Interpreting Integrals as Areas under Curves Nagwa Derivatives Integrals And The Area Under The Curve In particular, if we have a. 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. Just as definite integrals can be used to find the area under a curve, they can also be used to. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
areas under curves, definite integrals, and antiderivatives YouTube Derivatives Integrals And The Area Under The Curve To find the area between two curves defined by functions, integrate the difference of the functions. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. In particular, if we have a. The total area under a curve can be found using this formula. We will now study the area of very irregular figures.. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
Estimating Area Under Curve Using Trapezoidal Method Calculus YouTube Derivatives Integrals And The Area Under The Curve Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. The total area under a curve can be found using this. Derivatives Integrals And The Area Under The Curve.
From www.studocu.com
Area integrals 2 Area under or enclosed by the curve zadania 1 Derivatives Integrals And The Area Under The Curve Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. We will now study the area of very irregular figures. How to find the area under. Derivatives Integrals And The Area Under The Curve.
From www.wikihow.com
How to Find the Area Under a Curve Instructions & 7 Examples Derivatives Integrals And The Area Under The Curve The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. To find the area between two curves defined by functions, integrate the difference of the functions. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
Integration to find the area under a curve YouTube Derivatives Integrals And The Area Under The Curve The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. The total area under a curve can be found using this formula. How to find the area under a curve using integration. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing. Derivatives Integrals And The Area Under The Curve.
From socratic.org
What is an integral? + Example Derivatives Integrals And The Area Under The Curve The total area under a curve can be found using this formula. In particular, if we have a. To find the area between two curves defined by functions, integrate the difference of the functions. Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves.. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
C2 Integration (2) area under curves YouTube Derivatives Integrals And The Area Under The Curve How to find the area under a curve using integration. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. 6.1.3 determine the area of a region between two curves by. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
Finding area under a curve using integration YouTube Derivatives Integrals And The Area Under The Curve The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. The fundamental theorem of calculus, part 1. Derivatives Integrals And The Area Under The Curve.
From www.geeksforgeeks.org
Area Under The Curve Types, Formulas, Solved Examples, and FAQs Derivatives Integrals And The Area Under The Curve In particular, if we have a. The total area under a curve can be found using this formula. We will now study the area of very irregular figures. 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. To find the area between two curves defined by functions, integrate the difference of. Derivatives Integrals And The Area Under The Curve.
From www.nagwa.com
Question Video Finding the Area under the Curve of a Quadratic Derivatives Integrals And The Area Under The Curve How to find the area under a curve using integration. The total area under a curve can be found using this formula. Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. The fundamental theorem of calculus, part 1 shows the relationship between the. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
The Definite Integral as Area Under the Curve YouTube Derivatives Integrals And The Area Under The Curve The total area under a curve can be found using this formula. 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. To find the area between two curves defined by functions, integrate the difference of the functions. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and. Derivatives Integrals And The Area Under The Curve.
From www.cuemath.com
Area Under The Curve Formula Learn The Formula For Finding Area Under Derivatives Integrals And The Area Under The Curve To find the area between two curves defined by functions, integrate the difference of the functions. In particular, if we have a. The total area under a curve can be found using this formula. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. We will now study the area of very irregular figures.. Derivatives Integrals And The Area Under The Curve.
From www.met.reading.ac.uk
PPLATO Basic Mathematics Definite Integrals Derivatives Integrals And The Area Under The Curve Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. The total area under a curve can be found using this formula. The fundamental theorem of calculus, part. Derivatives Integrals And The Area Under The Curve.
From www.targetmathematics.com
Area under a Curve (Introduction to Definite Integral) Target Mathematics Derivatives Integrals And The Area Under The Curve How to find the area under a curve using integration. The total area under a curve can be found using this formula. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. We will now study the area of very irregular figures. To find the area between two curves defined by functions, integrate the. Derivatives Integrals And The Area Under The Curve.
From www.slideshare.net
Chapter 4 Integration Derivatives Integrals And The Area Under The Curve The total area under a curve can be found using this formula. We will now study the area of very irregular figures. How to find the area under a curve using integration. Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. 6.1.3 determine. Derivatives Integrals And The Area Under The Curve.
From www.onlinemathlearning.com
Calculus Area under a Curve (video lessons, examples, solutions) Derivatives Integrals And The Area Under The Curve The total area under a curve can be found using this formula. How to find the area under a curve using integration. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. 6.1.3 determine the area of a region between. Derivatives Integrals And The Area Under The Curve.
From xoomitre.blogspot.com
Integration Area Under Curve / AREA UNDER THE CURVE INTEGRATION Derivatives Integrals And The Area Under The Curve 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. How to find the area under a curve using integration. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and. Derivatives Integrals And The Area Under The Curve.
From www.cuemath.com
Area Under The Curve Method, Formula, Solved Examples, FAQs Derivatives Integrals And The Area Under The Curve In particular, if we have a. Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. To find the area between two curves defined by functions, integrate the difference of the functions. 6.1.3 determine the area of a region between two curves by integrating. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
Area Between Two Curves & Under Curve Respect to Y & X Calculus Derivatives Integrals And The Area Under The Curve The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. How to find the area under a curve using integration. In particular, if we have a. The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. We will now study the. Derivatives Integrals And The Area Under The Curve.
From www.sciencephoto.com
Integral calculus, area under curve Stock Image C008/3345 Science Derivatives Integrals And The Area Under The Curve To find the area between two curves defined by functions, integrate the difference of the functions. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. Just as definite integrals can be used to find the area under a curve,. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
MathTube Integration (4) Area Under A Curve Tutorial YouTube Derivatives Integrals And The Area Under The Curve Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. The fundamental theorem of calculus, part 1 shows the relationship between the. Derivatives Integrals And The Area Under The Curve.
From www.studocu.com
Area integrals Area under or enclosed by the curve zadania Derivatives Integrals And The Area Under The Curve In particular, if we have a. Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. The. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
Applications of integration area under a curve YouTube Derivatives Integrals And The Area Under The Curve The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. The fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of. Derivatives Integrals And The Area Under The Curve.
From stock.adobe.com
Vektorová grafika „Vector set of graphs with the demonstration of Derivatives Integrals And The Area Under The Curve 6.1.3 determine the area of a region between two curves by integrating with respect to the dependent variable. The total area under a curve can be found using this formula. We will now study the area of very irregular figures. To find the area between two curves defined by functions, integrate the difference of the functions. Intuitively, $\int_a^b f (x)dx$. Derivatives Integrals And The Area Under The Curve.
From en.wikipedia.org
Integral Wikipedia Derivatives Integrals And The Area Under The Curve Intuitively, $\int_a^b f (x)dx$ is the infinite sum of all rectangles with height $f (x)$ and width $dx$, and we are summing over all $x$ in the interval $ [a,b]$. To find the area between two curves defined by functions, integrate the difference of the functions. The total area under a curve can be found using this formula. The fundamental. Derivatives Integrals And The Area Under The Curve.
From www.scribd.com
Area under a curve Integral Function (Mathematics) Derivatives Integrals And The Area Under The Curve Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. We will now study the area of very irregular figures. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. The fundamental theorem of calculus, part 2 is. Derivatives Integrals And The Area Under The Curve.
From www.youtube.com
Integral Calculus lesson 4 How to find the area under a curve Derivatives Integrals And The Area Under The Curve Just as definite integrals can be used to find the area under a curve, they can also be used to find the area between two curves. We will now study the area of very irregular figures. The total area under a curve can be found using this formula. In particular, if we have a. 6.1.3 determine the area of a. Derivatives Integrals And The Area Under The Curve.