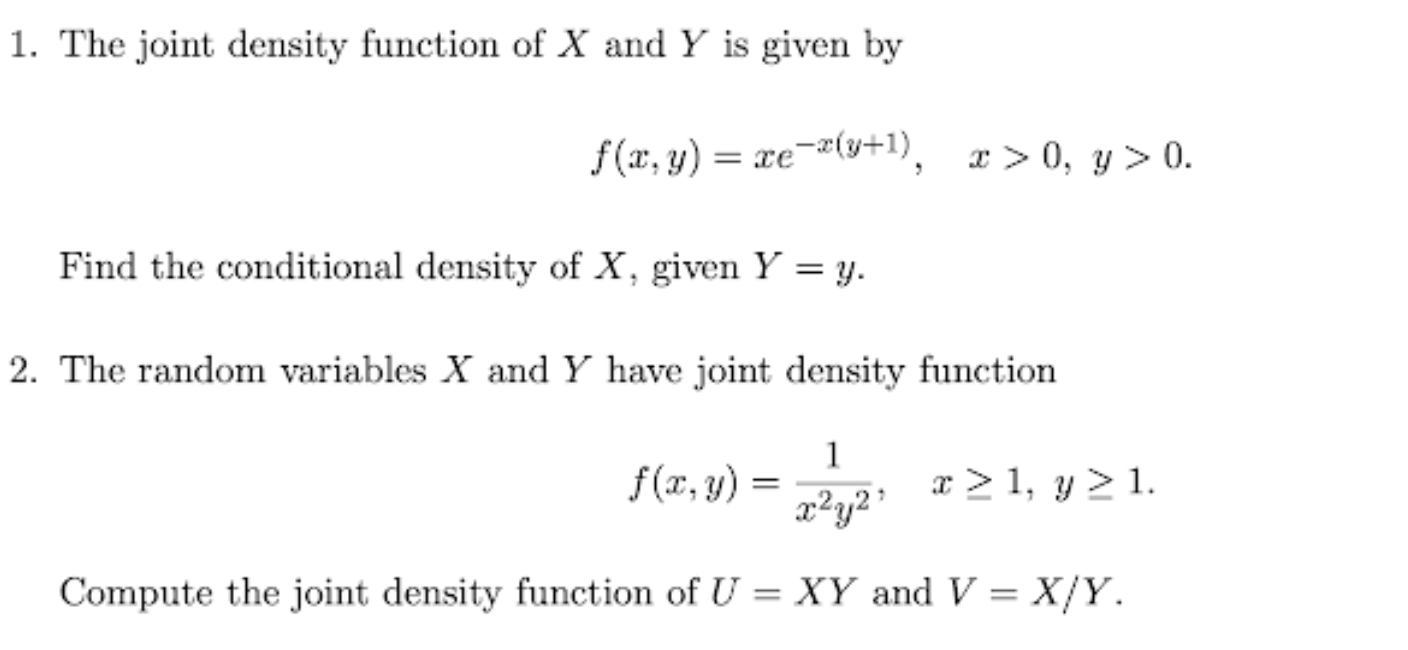Joint Density Function Independent . If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. What is the joint density function describing this scenario? And y representing the location of the dart. R2 → r, such that, for any set a ∈. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: The method used in example < 11.4 >,. The joint density can be used. Joint pdfs let x;y be.
from www.studyxapp.com
One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. The method used in example < 11.4 >,. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: Joint pdfs let x;y be. The joint density can be used. Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: And y representing the location of the dart. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. R2 → r, such that, for any set a ∈.
1 the joint density function of x and y is given by fx y te2 g1 t 0 y 0
Joint Density Function Independent Joint pdfs let x;y be. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. What is the joint density function describing this scenario? One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. R2 → r, such that, for any set a ∈. And y representing the location of the dart. The method used in example < 11.4 >,. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: Joint pdfs let x;y be. The joint density can be used. Two random variables x and y are jointly continuous if there exists a nonnegative function fxy:
From www.youtube.com
[Chapter 6] 2 Joint distribution of two continuous random variables Joint Density Function Independent R2 → r, such that, for any set a ∈. And y representing the location of the dart. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. Joint pdfs let x;y be. Find the joint density function (u;v) for (u;v),. Joint Density Function Independent.
From www.slideserve.com
PPT Joint Probability Distributions PowerPoint Presentation, free Joint Density Function Independent What is the joint density function describing this scenario? Joint pdfs let x;y be. And y representing the location of the dart. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: The joint density can be used. R2 → r, such that, for any set a ∈. Find. Joint Density Function Independent.
From calcworkshop.com
Joint Continuous Random Variables (w/ 5+ Examples!) Joint Density Function Independent Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. R2 → r, such that, for any set a ∈. What is the joint density function describing this scenario? And y representing the location of the dart. The method used in example < 11.4 >,. If continuous random variables \(x\) and \(y\). Joint Density Function Independent.
From www.chegg.com
Solved The joint density function of the random variables X Joint Density Function Independent The method used in example < 11.4 >,. One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. What is the joint density function describing this scenario? Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: The. Joint Density Function Independent.
From www.youtube.com
Joint Density Function YouTube Joint Density Function Independent What is the joint density function describing this scenario? If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. And y representing the location of the dart. One of the entries of a continuous random vector, when considered in isolation, can. Joint Density Function Independent.
From statlect.com
Joint probability density function Definition, explanation, examples Joint Density Function Independent If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. The joint density can be used. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: The method used in. Joint Density Function Independent.
From www.chegg.com
Solved 5. The joint density function of X and Y is given by Joint Density Function Independent If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: And y representing the location of the dart. R2 → r, such that, for any set a ∈. The method used in example. Joint Density Function Independent.
From www.numerade.com
SOLVEDLet k e R and suppose that a twodimensional continuous random Joint Density Function Independent And y representing the location of the dart. R2 → r, such that, for any set a ∈. One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. The method used in example < 11.4 >,. What is the joint density function describing this. Joint Density Function Independent.
From www.studyxapp.com
1 the joint density function of x and y is given by fx y te2 g1 t 0 y 0 Joint Density Function Independent Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning. Joint Density Function Independent.
From pdfprof.com
JOINT SOL ET mUR Joint Density Function Independent What is the joint density function describing this scenario? If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. R2 → r, such that, for any set a ∈. The method used in example < 11.4 >,. The joint density can. Joint Density Function Independent.
From www.chegg.com
Solved The joint density function of the random variables X Joint Density Function Independent The joint density can be used. What is the joint density function describing this scenario? If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: And y representing the location of the dart. Joint pdfs let x;y be. If continuous random variables \(x\) and \(y\) are defined on the. Joint Density Function Independent.
From www.slideserve.com
PPT Joint Density Function PowerPoint Presentation, free download Joint Density Function Independent One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. And y representing the location of the dart. What is the joint density function describing this scenario? If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their. Joint Density Function Independent.
From www.chegg.com
Solved Let X and Y have the joint probability density Joint Density Function Independent One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. What is the joint density function describing this scenario? And y representing the location of the dart. Joint pdfs let x;y be. The joint density can be used. R2 → r, such that, for. Joint Density Function Independent.
From stats.stackexchange.com
Explanation of Joint Probability and Independence Cross Validated Joint Density Function Independent If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: The joint density can be used. Joint pdfs let x;y be. What is the joint density function describing this scenario? R2 → r,. Joint Density Function Independent.
From www.chegg.com
Solved The joint density function of the random variables X Joint Density Function Independent Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. The method used in example < 11.4 >,. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: R2 → r, such that, for any set a ∈. And y representing. Joint Density Function Independent.
From www.youtube.com
L09.10 Joint CDFs YouTube Joint Density Function Independent One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. The method used in example < 11.4 >,. The joint density can be used. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density. Joint Density Function Independent.
From www.numerade.com
SOLVEDSuppose X and Y have joint density function 3 (ry + yP) if 0 Joint Density Function Independent R2 → r, such that, for any set a ∈. And y representing the location of the dart. Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: Joint pdfs let x;y be.. Joint Density Function Independent.
From www.youtube.com
4.1 & 4.2 Multiple Random Variables and Joint Distribution (CDF) YouTube Joint Density Function Independent Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: The joint density can be used. Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. The method used in example < 11.4 >,. If continuous random variables \(x\) and \(y\) are defined on the same. Joint Density Function Independent.
From www.coursehero.com
[Solved] If the joint density function of X and Y is given f(x, y Joint Density Function Independent R2 → r, such that, for any set a ∈. Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: One of the entries of a continuous random vector, when considered. Joint Density Function Independent.
From www.chegg.com
Let X and Y be independent identically distributed Joint Density Function Independent Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: The method used in example < 11.4 >,. The joint density can be used. Two random variables x and y are. Joint Density Function Independent.
From www.youtube.com
Joint Probability Density Functions YouTube Joint Density Function Independent Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. Joint pdfs let x;y be. The joint density can be used. And y. Joint Density Function Independent.
From calcworkshop.com
Joint Continuous Random Variables (w/ 5+ Examples!) Joint Density Function Independent R2 → r, such that, for any set a ∈. The method used in example < 11.4 >,. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. One of the entries of a continuous random vector, when considered in isolation,. Joint Density Function Independent.
From www.quora.com
What is meaning of [math]y[/math]axis value when you graph a Joint Density Function Independent One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. What is the joint density function describing this scenario? The method used in example < 11.4. Joint Density Function Independent.
From brainly.com
. The joint density function of X and Y is given by f ( x , y ) = x e − Joint Density Function Independent If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: Joint pdfs let x;y be. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. What is the joint density. Joint Density Function Independent.
From calcworkshop.com
Joint Continuous Random Variables (w/ 5+ Examples!) Joint Density Function Independent If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning. Joint Density Function Independent.
From www.chegg.com
Solved Let X And Y Have The Joint Probability Density Fun... Joint Density Function Independent And y representing the location of the dart. The method used in example < 11.4 >,. What is the joint density function describing this scenario? R2 → r, such that, for any set a ∈. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a. Joint Density Function Independent.
From www.chegg.com
Solved 4. Let Yi, } 2,, Yn be independent, uniformly Joint Density Function Independent R2 → r, such that, for any set a ∈. Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: One of the entries of a continuous random vector, when considered in isolation, can be described by its probability density function, which is called marginal density. The joint density can be used. What is. Joint Density Function Independent.
From www.slideserve.com
PPT Joint Density Function PowerPoint Presentation, free download Joint Density Function Independent Joint pdfs let x;y be. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split it as: Find the joint density function. Joint Density Function Independent.
From www.chegg.com
Solved 4. (20 pts) The joint density function of the random Joint Density Function Independent If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. The joint density can be used. If $x$ and $y$ are independent then. Joint Density Function Independent.
From quizlet.com
The joint probability density function of X and Y is given b Quizlet Joint Density Function Independent Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: What is the joint density function describing this scenario? If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. Joint pdfs let x;y be. One. Joint Density Function Independent.
From www.chegg.com
Solved The joint density function of the random variables X Joint Density Function Independent The method used in example < 11.4 >,. What is the joint density function describing this scenario? The joint density can be used. Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. And y representing the location of the dart. If $x$ and $y$ are independent then the joint density kernel. Joint Density Function Independent.
From www.chegg.com
Solved Joint probability mass function p(a, b) = P(X = a, Y Joint Density Function Independent Joint pdfs let x;y be. Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous function, denoted. R2 → r, such that, for any set a ∈.. Joint Density Function Independent.
From www.vrogue.co
Two Random Variables X And Have The Following Joint P vrogue.co Joint Density Function Independent What is the joint density function describing this scenario? Find the joint density function (u;v) for (u;v), under the assumption that the quantity = ad bcis nonzero. R2 → r, such that, for any set a ∈. Joint pdfs let x;y be. If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint. Joint Density Function Independent.
From www.chegg.com
Solved 6. Suppose the joint probability density function for Joint Density Function Independent The method used in example < 11.4 >,. Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: What is the joint density function describing this scenario? If continuous random variables \(x\) and \(y\) are defined on the same sample space \(s\), then their joint probability density function (joint pdf) is a piecewise continuous. Joint Density Function Independent.
From www.youtube.com
MA 381 Section 8.1 Joint Probability Density Functions YouTube Joint Density Function Independent Two random variables x and y are jointly continuous if there exists a nonnegative function fxy: What is the joint density function describing this scenario? The method used in example < 11.4 >,. And y representing the location of the dart. If $x$ and $y$ are independent then the joint density kernel will be seperable, meaning that you can split. Joint Density Function Independent.