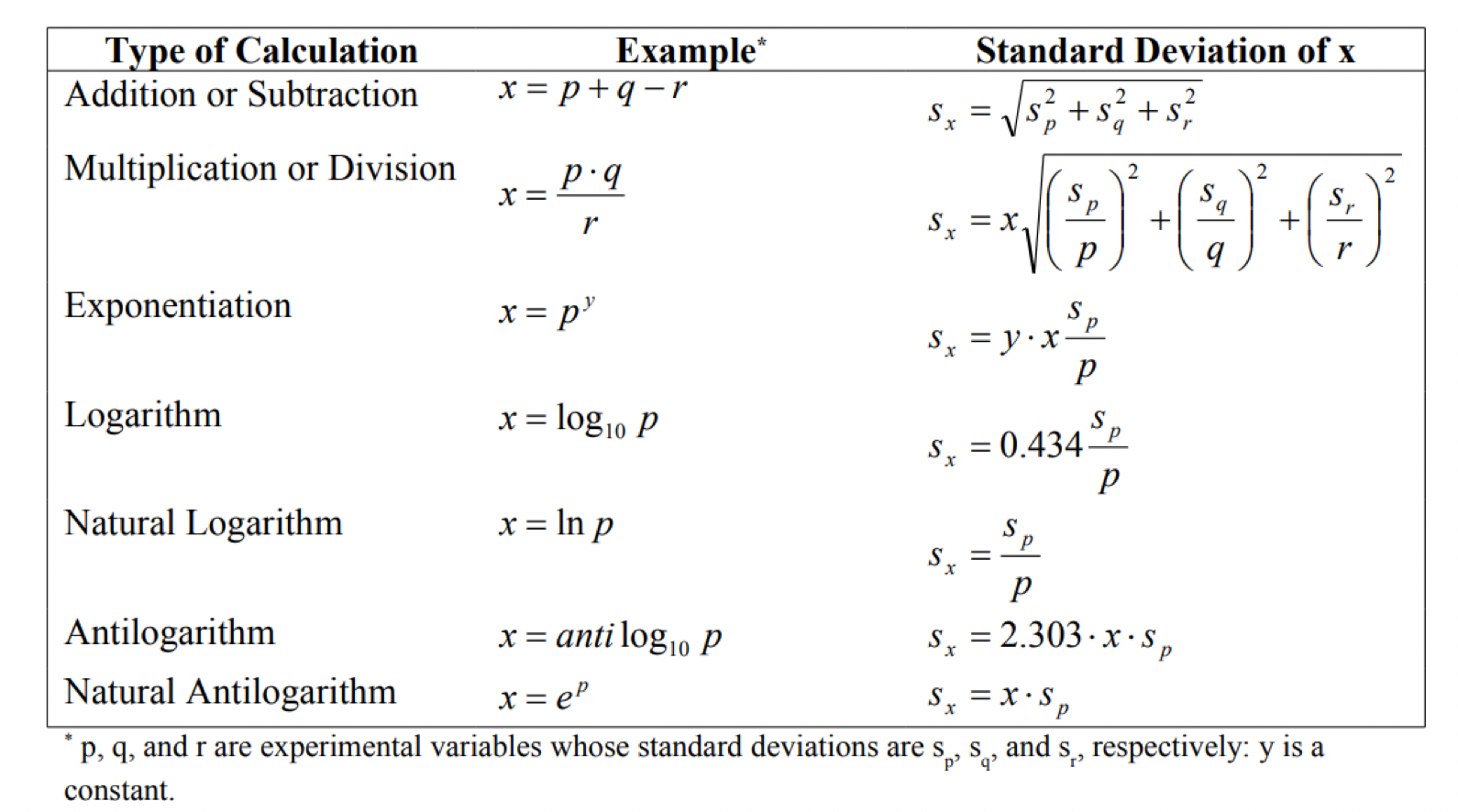
Logarithmic Uncertainty . The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; You can also reduce uncertainty by. You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. At some point, the nonlinearities can no longer be ignored. Propagating uncertainties through the logarithms. The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate. We have been using the monte carlo method to propagate errors thus far,. A formula for propagating uncertainties through a natural logarithm. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently.
from www.chegg.com
Propagating uncertainties through the logarithms. You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. We have been using the monte carlo method to propagate errors thus far,. At some point, the nonlinearities can no longer be ignored. The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. A formula for propagating uncertainties through a natural logarithm. In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. You can also reduce uncertainty by.
Solved Using the table as a reference, propagate
Logarithmic Uncertainty The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; You can also reduce uncertainty by. Propagating uncertainties through the logarithms. We have been using the monte carlo method to propagate errors thus far,. Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. At some point, the nonlinearities can no longer be ignored. In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. A formula for propagating uncertainties through a natural logarithm.
From www.researchgate.net
Uncertainty related to the difference in the resolution between Logarithmic Uncertainty A formula for propagating uncertainties through a natural logarithm. We have been using the monte carlo method to propagate errors thus far,. The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate. In this section, we will be converting our (l, t) data points with uncertainties to. Logarithmic Uncertainty.
From www.numerade.com
SOLVED Perform the calculations and determine the absolute and percent Logarithmic Uncertainty Propagating uncertainties through the logarithms. A formula for propagating uncertainties through a natural logarithm. You can also reduce uncertainty by. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the. Logarithmic Uncertainty.
From www.animalia-life.club
Logarithm Formula Logarithmic Uncertainty In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. A formula for propagating uncertainties through a natural logarithm. Yet another type of uncertainty principle is the. Logarithmic Uncertainty.
From www.researchgate.net
Sharp Pitt’s inequality and Beckner’s logarithmic uncertainty principle Logarithmic Uncertainty The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points. Logarithmic Uncertainty.
From www.researchgate.net
Standard uncertainty associated with nonreproducibility (logarithmic Logarithmic Uncertainty You can also reduce uncertainty by. In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. Propagating uncertainties through the logarithms. A formula for propagating uncertainties through. Logarithmic Uncertainty.
From www.slideserve.com
PPT Chapters 3 Uncertainty PowerPoint Presentation, free download Logarithmic Uncertainty The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. A formula for propagating uncertainties through a natural logarithm. At some point, the nonlinearities can no longer be ignored. The uncertainty is a range of values around a measurement within which the true value is. Logarithmic Uncertainty.
From www.youtube.com
SOLVING LOGARITHMIC EQUATIONS FINDING THE VALUE OF X YouTube Logarithmic Uncertainty You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; A formula for propagating uncertainties through a natural logarithm. We have been using the monte carlo method to propagate errors thus far,. You can. Logarithmic Uncertainty.
From www.researchgate.net
(PDF) Uncertainty and Prior Assumptions, Rather Than Innate Logarithmic Logarithmic Uncertainty In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. At some point, the nonlinearities can no longer be ignored. You can reduce uncertainty by fixing. Logarithmic Uncertainty.
From www.researchgate.net
Pitt’s Inequality and Logarithmic Uncertainty Principle for the Logarithmic Uncertainty Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. You can reduce uncertainty by fixing one end of a ruler as only the. Logarithmic Uncertainty.
From www.researchgate.net
Semilogarithmic plot of uncertainty in quadrature variances [((X + ) 2 Logarithmic Uncertainty The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. A formula for propagating uncertainties through a natural logarithm. You can also reduce uncertainty by. Propagating uncertainties through the logarithms. The general rule. Logarithmic Uncertainty.
From www.researchgate.net
(PDF) Logarithmic uncertainty principle for the Hankel transform Logarithmic Uncertainty The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. A formula for propagating uncertainties through a natural logarithm. We have been. Logarithmic Uncertainty.
From www.chegg.com
Solved Using the table as a reference, propagate Logarithmic Uncertainty In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. We have been using the monte carlo method to propagate errors thus far,. Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. Propagating uncertainties through. Logarithmic Uncertainty.
From wikiblog88.blogspot.com
Percent Uncertainty Formula The Area Of A Rectangle If the percent Logarithmic Uncertainty Propagating uncertainties through the logarithms. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; At some point, the nonlinearities can no longer be ignored. You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. We have been using the monte carlo method to. Logarithmic Uncertainty.
From www.researchgate.net
Top to bottom logarithmicscale sample by sample inversion Logarithmic Uncertainty At some point, the nonlinearities can no longer be ignored. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. A formula for propagating uncertainties through a natural logarithm. The general rule is that. Logarithmic Uncertainty.
From www.youtube.com
Log—Absolute & Percent Relative Uncertainty YouTube Logarithmic Uncertainty We have been using the monte carlo method to propagate errors thus far,. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; At some point, the nonlinearities can no longer be ignored. A formula for propagating uncertainties through a natural logarithm. Propagating uncertainties through the logarithms. The general rule is that when you. Logarithmic Uncertainty.
From www.researchgate.net
(PDF) A Variation on Uncertainty Principle and Logarithmic Uncertainty Logarithmic Uncertainty At some point, the nonlinearities can no longer be ignored. The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate. In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. Propagating uncertainties through the. Logarithmic Uncertainty.
From www.researchgate.net
Logarithmic posterior uncertainties of the different reconstructions Logarithmic Uncertainty The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate. You can also reduce uncertainty by. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. Yet another type of uncertainty principle. Logarithmic Uncertainty.
From www.youtube.com
How to calculate absolute uncertainties in log values YouTube Logarithmic Uncertainty At some point, the nonlinearities can no longer be ignored. You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. Propagating uncertainties through the logarithms. A formula for propagating uncertainties through a natural logarithm. In this section, we will be converting our (l, t) data points with uncertainties to (ln. Logarithmic Uncertainty.
From www.scribd.com
Environmental Uncertainty & Porter PDF Logarithm Regression Analysis Logarithmic Uncertainty A formula for propagating uncertainties through a natural logarithm. The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate. Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. You can reduce uncertainty by fixing one. Logarithmic Uncertainty.
From www.scribd.com
Content PDF Logarithm Uncertainty Logarithmic Uncertainty You can also reduce uncertainty by. A formula for propagating uncertainties through a natural logarithm. We have been using the monte carlo method to propagate errors thus far,. In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. The uncertainty is a range of values around a. Logarithmic Uncertainty.
From www.researchgate.net
Effect of digitization uncertainty in linear, instead of logarithmic Logarithmic Uncertainty The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. A formula for propagating uncertainties through a natural logarithm. The uncertainty is a range. Logarithmic Uncertainty.
From www.researchgate.net
(PDF) Logarithmic uncertainty principles for the Hankel wavelet transform Logarithmic Uncertainty A formula for propagating uncertainties through a natural logarithm. In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. Propagating uncertainties through the logarithms. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for. Logarithmic Uncertainty.
From www.scruffs.shetland.co.uk
Logarithms Logarithmic Uncertainty The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; A formula for propagating uncertainties through a natural logarithm. Propagating uncertainties through the logarithms. We have been using the monte carlo method to propagate errors thus far,. You can also reduce uncertainty by. The uncertainty is a range of values around a measurement within. Logarithmic Uncertainty.
From www.researchgate.net
Illustration of the relative reconstruction uncertainty on a Logarithmic Uncertainty Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. You can also reduce uncertainty by. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; The uncertainty is a range of values around a measurement within which the true value is expected. Logarithmic Uncertainty.
From www.scribd.com
Stretch and Challenge PDF Uncertainty Logarithm Logarithmic Uncertainty We have been using the monte carlo method to propagate errors thus far,. Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. Propagating. Logarithmic Uncertainty.
From www.researchgate.net
Amplifications in drought hazard with growth exponent λ > 1. Scatter Logarithmic Uncertainty Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. At some point, the nonlinearities can no longer be ignored. We have been using the monte carlo method to propagate errors thus far,. Propagating uncertainties through the logarithms. A formula for propagating uncertainties through a natural logarithm. The uncertainty. Logarithmic Uncertainty.
From www.researchgate.net
Per‐pixel uncertainty (in natural logarithmic scale) of the annual mean Logarithmic Uncertainty The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. Propagating uncertainties through the logarithms. You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. In this section, we will be converting our (l, t). Logarithmic Uncertainty.
From www.semanticscholar.org
Figure 1.1 from Logarithmic Sobolev and Shannon's inequalities and an Logarithmic Uncertainty At some point, the nonlinearities can no longer be ignored. You can reduce uncertainty by fixing one end of a ruler as only the uncertainty in one reading is included. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. Yet another type of uncertainty. Logarithmic Uncertainty.
From www.slideserve.com
PPT Derivatives of Logarithmic Functions PowerPoint Presentation Logarithmic Uncertainty In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. You can also reduce uncertainty by. We have been using the monte carlo method to propagate errors thus far,. At some point, the nonlinearities can no longer be ignored. The reason for this is that the logarithm. Logarithmic Uncertainty.
From www.youtube.com
A Level Physics All Exam Boards SHM Uncertainty in Logarithms in Logarithmic Uncertainty Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties.. Logarithmic Uncertainty.
From www.researchgate.net
(PDF) Logarithmic Uncertainty Relations for Odd or Even Signals Logarithmic Uncertainty The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. Propagating uncertainties through the logarithms. We have been using the monte carlo method to propagate errors thus far,. At some point, the nonlinearities. Logarithmic Uncertainty.
From www.youtube.com
Plotting Uncertainty in log log plot YouTube Logarithmic Uncertainty At some point, the nonlinearities can no longer be ignored. In this section, we will be converting our (l, t) data points with uncertainties to (ln (l), ln (t/2π)) data points with uncertainties. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; You can reduce uncertainty by fixing one end of a ruler. Logarithmic Uncertainty.
From www.youtube.com
Q2b Tables Uncertainties with log and ln A2 Practical Paper 5 Logarithmic Uncertainty Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. The reason for this is that the logarithm becomes increasingly nonlinear as its argument approaches zero; The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for. Logarithmic Uncertainty.
From www.researchgate.net
Uncertainty Scores in logarithmic scales from various uncertainty Logarithmic Uncertainty Propagating uncertainties through the logarithms. We have been using the monte carlo method to propagate errors thus far,. Yet another type of uncertainty principle is the logarithmic version conjectured by hirschman [21] and proven by beckner [4] and independently. The general rule is that when you have a value $g$ that depends of another value $f$ then if you write. Logarithmic Uncertainty.
From www.researchgate.net
Uncertainty of electron density in logarithmic scale (first row), zonal Logarithmic Uncertainty The general rule is that when you have a value $g$ that depends of another value $f$ then if you write $u(g)$ for the incertitude. You can also reduce uncertainty by. We have been using the monte carlo method to propagate errors thus far,. At some point, the nonlinearities can no longer be ignored. A formula for propagating uncertainties through. Logarithmic Uncertainty.