Equivalent Categories . Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). 37 rows there is also a notion of equivalence between model categories: The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An equivalence between categories a and b consists of a pair of functors f: An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. These can be understood to some. B !a and a pair of natural isomorphisms :
from www.chegg.com
The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. An equivalence between categories a and b consists of a pair of functors f: 37 rows there is also a notion of equivalence between model categories: Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). B !a and a pair of natural isomorphisms : These can be understood to some. An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic.
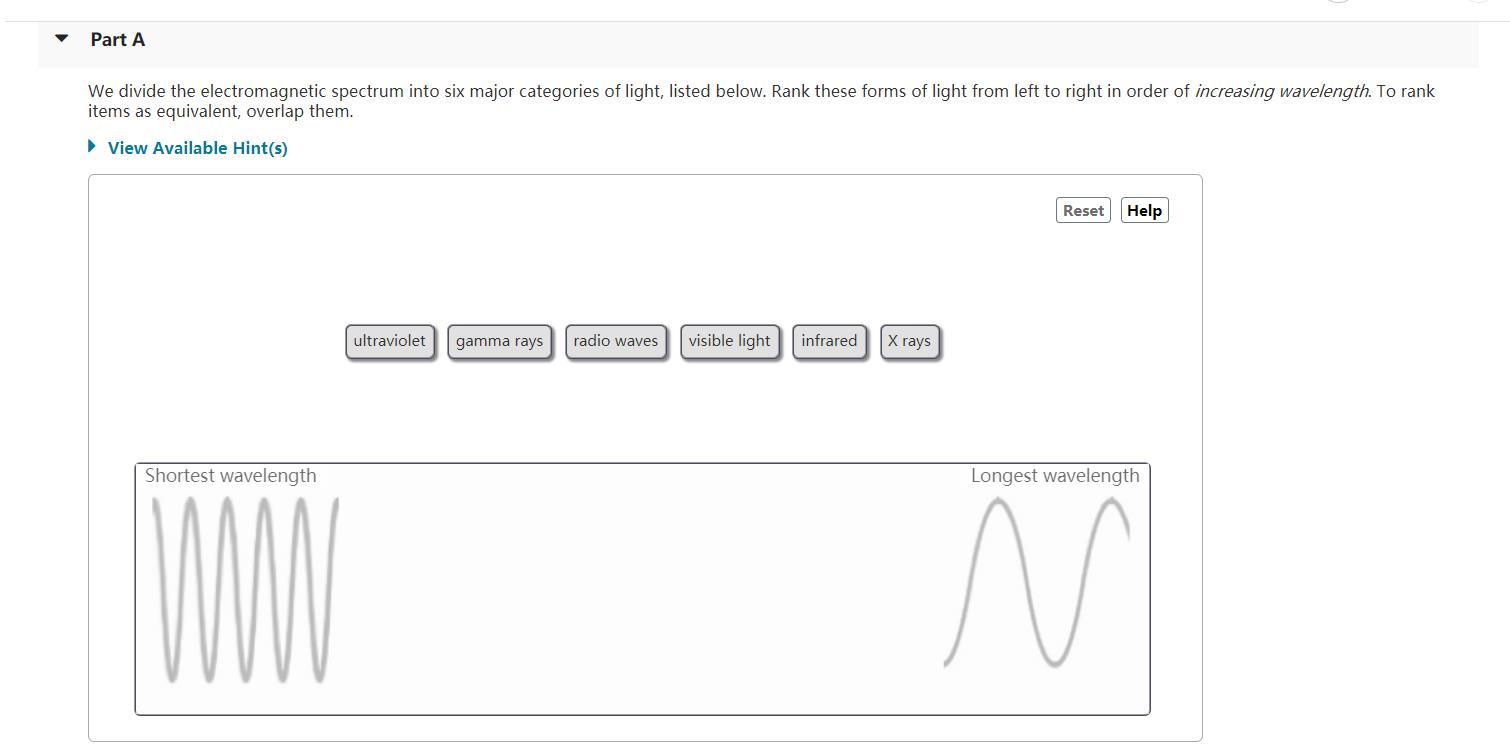
Solved Part A We divide the spectrum into
Equivalent Categories The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An equivalence between categories a and b consists of a pair of functors f: We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. B !a and a pair of natural isomorphisms : Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). 37 rows there is also a notion of equivalence between model categories: These can be understood to some.
From www.chegg.com
Solved Part A We divide the spectrum into Equivalent Categories We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. 37 rows there is also a notion of equivalence between model categories: The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. These can be understood to some. B !a and a pair of natural isomorphisms : An. Equivalent Categories.
From mage02.technogym.com
Equivalent Fraction Chart Equivalent Categories The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. These can be understood to some. We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. An equivalence between categories a and b consists of a pair of functors f: An extension of the concept of an isomorphism. Equivalent Categories.
From www.coursehero.com
[Solved] Equivalent units of production for all three cost categories Equivalent Categories These can be understood to some. Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An equivalence between categories a. Equivalent Categories.
From www.etsy.com
Equivalent Fractions Math Anchor Chart, Strategy Poster With Lamination Equivalent Categories These can be understood to some. Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). 37 rows there is also a notion of equivalence between model categories: The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. We exhibited an explicit example involving the category $\mathbf{mat}$. Equivalent Categories.
From donsteward.blogspot.com
MEDIAN Don Steward mathematics teaching equivalent fractions shaded Equivalent Categories An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). B !a and a pair of natural isomorphisms : The concept of equivalence of categories is the correct category theoretic notion. Equivalent Categories.
From www.eurosteel.co.za
Stainless Steel Technical Data Eurosteel Equivalent Categories We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. 37 rows there is also a notion of equivalence between model categories: An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. The concept of equivalence of categories is the correct category. Equivalent Categories.
From www.pharmaspecialists.com
Therapeutic Equivalence Evaluations Codes Equivalent Categories An equivalence between categories a and b consists of a pair of functors f: Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). These can be understood to some. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. 37 rows there is also a notion. Equivalent Categories.
From www.semanticscholar.org
Figure 1 from CLUSTERING NOMINAL DATA WITH EQUIVALENT CATEGORIES Equivalent Categories 37 rows there is also a notion of equivalence between model categories: We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. B !a and a pair of natural isomorphisms : These can be understood to some. An equivalence between categories a and b consists of a pair of functors f: The concept of. Equivalent Categories.
From www.vedantu.com
Equivalent Ratio Learn Definition, Practice Questions, Facts and Examples Equivalent Categories The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. These can be understood to some. B !a and a pair of natural isomorphisms : We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. An equivalence between categories a and b consists of a pair of functors. Equivalent Categories.
From www.alamyimages.fr
Symboles de conduire subdivisées en différentes catégories Image Equivalent Categories Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). These can be understood to some. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. 37 rows there is also a notion of equivalence between model categories: B !a and a pair of natural isomorphisms :. Equivalent Categories.
From www.coursehero.com
[Solved] Equivalent units of production for all three cost categories Equivalent Categories B !a and a pair of natural isomorphisms : We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). 37 rows there is also a notion of equivalence between model categories: An extension of the concept of. Equivalent Categories.
From mavink.com
Metabolic Equivalent Met Activities Chart Equivalent Categories B !a and a pair of natural isomorphisms : An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. An equivalence between categories a and b consists of a pair of functors f: These can be understood to some. We exhibited an explicit example involving the category $\mathbf{mat}$. Equivalent Categories.
From dave-lam.blogspot.com
Gcse Grades Percentage Equivalents GCSEs 2020 The 91 grading system Equivalent Categories 37 rows there is also a notion of equivalence between model categories: The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the. Equivalent Categories.
From www.madebyteachers.com
Ratio Worksheets Equivalent Ratio Worksheets Write two equivalent Equivalent Categories B !a and a pair of natural isomorphisms : 37 rows there is also a notion of equivalence between model categories: We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An extension of the concept of an. Equivalent Categories.
From www.media4math.com
Student Tutorial Ratios, Proportions, and Percents Definitions Equivalent Categories B !a and a pair of natural isomorphisms : We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. An equivalence between categories a and b consists of a pair of functors f: An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of. Equivalent Categories.
From www.template.net
Free Equivalent Fractions Anchor Chart Download in PDF, Illustrator Equivalent Categories These can be understood to some. B !a and a pair of natural isomorphisms : We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An equivalence between categories a and b consists of a pair of functors. Equivalent Categories.
From www.printablee.com
Equivalent Fractions Chart 10 Free PDF Printables Printablee Equivalent Categories An equivalence between categories a and b consists of a pair of functors f: Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). B !a and a pair of natural isomorphisms : The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. We exhibited an explicit. Equivalent Categories.
From www.ais.edu.hk
GRADE LEVEL EQUIVALENT GUIDE American International School Equivalent Categories Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. B !a and a pair of natural isomorphisms : An equivalence between categories a and b consists of a pair of. Equivalent Categories.
From www.printablee.com
Equivalent Fractions Chart 10 Free PDF Printables Printablee Equivalent Categories An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. B !a and a pair of natural isomorphisms : We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. An equivalence between categories a and b consists of a pair of functors. Equivalent Categories.
From www.researchgate.net
Categories of standards and equivalent concepts in the ontology Equivalent Categories The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An equivalence between categories a and b consists of a pair of functors f: An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. B !a and a pair of natural isomorphisms. Equivalent Categories.
From clipground.com
Equivalent clipart Clipground Equivalent Categories An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. An equivalence between categories a and b consists of a pair of functors f: The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. B !a and a pair of natural isomorphisms. Equivalent Categories.
From www.datacamp.com
AWS, Azure and GCP Service Comparison for Data Science & AI DataCamp Equivalent Categories B !a and a pair of natural isomorphisms : These can be understood to some. We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An equivalence between categories a and b consists of a pair of functors. Equivalent Categories.
From studylib.net
4 Equivalent Categories. Equivalent Categories These can be understood to some. An equivalence between categories a and b consists of a pair of functors f: An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). The. Equivalent Categories.
From www.reddit.com
Are there equivalent categories for women with regard to being “alpha Equivalent Categories We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. These can be understood to some.. Equivalent Categories.
From www.researchgate.net
Actions, activities and equivalent ICF categories in the ADLTaxonomy Equivalent Categories An equivalence between categories a and b consists of a pair of functors f: An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. 37 rows there is also a notion of equivalence between model categories: B !a and a pair of natural isomorphisms : The concept of. Equivalent Categories.
From www.researchgate.net
S&P, Moody's and Fitch rating systems and linear transformations Equivalent Categories These can be understood to some. An equivalence between categories a and b consists of a pair of functors f: An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. B !a and a pair of natural isomorphisms : 37 rows there is also a notion of equivalence. Equivalent Categories.
From stock.adobe.com
equivalent fractions chart in mathematics Stock Vector Adobe Stock Equivalent Categories An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. 37 rows there is also a notion of equivalence between model categories: An equivalence between categories a and b consists of a. Equivalent Categories.
From www.cazoommaths.com
Equivalent Fractions (C) Worksheet Cazoom Maths Worksheets Equivalent Categories An equivalence between categories a and b consists of a pair of functors f: An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. Some pretty big results in mathematics can be. Equivalent Categories.
From www.etsy.com
Equivalent Fractions Anchor Chart, Printed on FABRIC Anchor Charts Are Equivalent Categories B !a and a pair of natural isomorphisms : The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An equivalence between categories a and b consists of a pair of functors f: An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of. Equivalent Categories.
From www.canadianschool.it
Canadian School of Milan Grade Equivalents Equivalent Categories We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. B !a and a pair. Equivalent Categories.
From www.cgpplus.co.uk
Comparing and Ordering Fractions (Year 3) CGP Plus Equivalent Categories B !a and a pair of natural isomorphisms : 37 rows there is also a notion of equivalence between model categories: An equivalence between categories a and b consists of a pair of functors f: Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). We exhibited an explicit example involving the category. Equivalent Categories.
From www.teachersparadise.com
TeachersParadise TREND Equivalent Fractions Learning Chart, 17" x 22 Equivalent Categories These can be understood to some. Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the. Equivalent Categories.
From mavink.com
Equivalent Fractions Chart Equivalent Categories We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. B !a and a pair of natural isomorphisms : An equivalence between categories a and b consists of a pair of functors f: An extension of the concept. Equivalent Categories.
From kto5education.com
Equivalent Ratios Worksheets FREE Download Equivalent Categories 37 rows there is also a notion of equivalence between model categories: Some pretty big results in mathematics can be expressed as equivalence of categories (or rather, as adjunctions). We exhibited an explicit example involving the category $\mathbf{mat}$ of matrices over $\mathbb{r}$ and the category. An equivalence between categories a and b consists of a pair of functors f: The. Equivalent Categories.
From www.inkl.com
GCSE grades explained equivalent results and… Equivalent Categories The concept of equivalence of categories is the correct category theoretic notion of “sameness” of categories. An extension of the concept of an isomorphism of categories brought about, first of all, by the presence of classes of isomorphic. 37 rows there is also a notion of equivalence between model categories: These can be understood to some. Some pretty big results. Equivalent Categories.