Associative Law In Logic Gates . Likewise, the biconditional ↔ is. A and (b and c) ≡ (a and b) and c and in notation, we would write: The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Associative law this law says: Many logical laws are similar to algebraic laws. Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. Some logical operators are associative: In this chapter, we will learn about. Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. A λ (b λ c) ≡ (a λ b) λ c. For example, there is a logical law corresponding to the associative law of. Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well to addition and multiplication.
from webdocs.cs.ualberta.ca
A and (b and c) ≡ (a and b) and c and in notation, we would write: Likewise, the biconditional ↔ is. Associative law this law says: The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well to addition and multiplication. Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. In this chapter, we will learn about. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. For example, there is a logical law corresponding to the associative law of. Many logical laws are similar to algebraic laws.
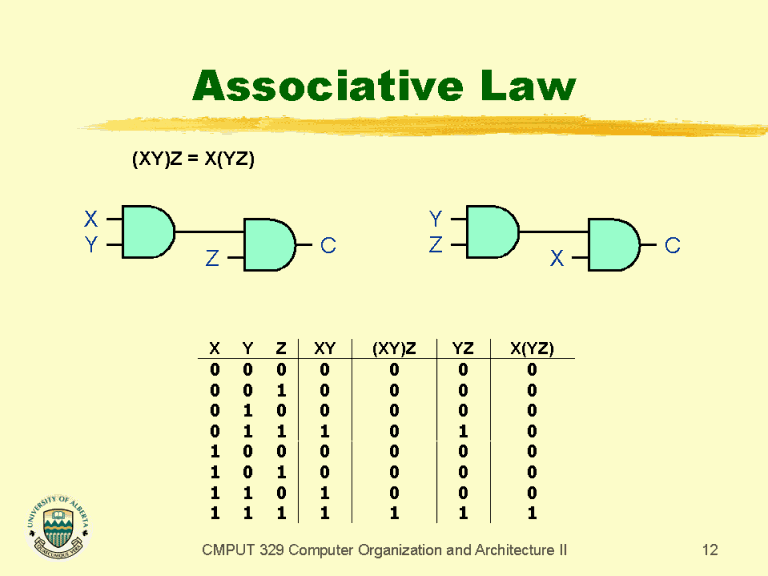
Associative Law
Associative Law In Logic Gates A λ (b λ c) ≡ (a λ b) λ c. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. A and (b and c) ≡ (a and b) and c and in notation, we would write: Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. Some logical operators are associative: Associative law this law says: A λ (b λ c) ≡ (a λ b) λ c. Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. Many logical laws are similar to algebraic laws. For example, there is a logical law corresponding to the associative law of. Likewise, the biconditional ↔ is. In this chapter, we will learn about. The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well to addition and multiplication.
From www.slideserve.com
PPT Chapter 2 Boolean Algebra and Logic Gates PowerPoint Presentation Associative Law In Logic Gates Associative law this law says: Likewise, the biconditional ↔ is. A λ (b λ c) ≡ (a λ b) λ c. Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. The boolean algebra uses. Associative Law In Logic Gates.
From mungfali.com
Truth Table Of Logic Gates Associative Law In Logic Gates A λ (b λ c) ≡ (a λ b) λ c. The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. In this chapter, we will learn about. A and (b and c) ≡ (a and b) and c and in notation, we would write: For example, there. Associative Law In Logic Gates.
From www.youtube.com
What is Associative law of Sets ? YouTube Associative Law In Logic Gates Many logical laws are similar to algebraic laws. A and (b and c) ≡ (a and b) and c and in notation, we would write: Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. A λ (b λ c) ≡ (a λ b) λ c. Some logical operators. Associative Law In Logic Gates.
From www.youtube.com
Properties of various Logic Gates Commutative, Associative Associative Law In Logic Gates Many logical laws are similar to algebraic laws. Associative law this law says: Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. A and (b and c). Associative Law In Logic Gates.
From www.slideserve.com
PPT Boolean Algebra and Logic Simplification PowerPoint Presentation Associative Law In Logic Gates In this chapter, we will learn about. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well to addition and multiplication. Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit. Associative Law In Logic Gates.
From webdocs.cs.ualberta.ca
Associative Law Associative Law In Logic Gates A and (b and c) ≡ (a and b) and c and in notation, we would write: A λ (b λ c) ≡ (a λ b) λ c. Associative law this law says: Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Each law of the boolean algebra can be interpreted as an operation performed. Associative Law In Logic Gates.
From www.youtube.com
What is Logic Gate ? Logic Gates Explained YouTube Associative Law In Logic Gates Associative law this law says: A λ (b λ c) ≡ (a λ b) λ c. In this chapter, we will learn about. Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well to addition and multiplication. For example, there is a logical law corresponding to the associative law of. Likewise, the. Associative Law In Logic Gates.
From www.cburch.com
Logic & circuits Associative Law In Logic Gates Many logical laws are similar to algebraic laws. The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. A λ (b λ c) ≡ (a λ b) λ c. Some logical operators are associative: In this chapter, we will learn about. Associative law this law says: For example,. Associative Law In Logic Gates.
From www.slideserve.com
PPT Boolean Algebra and Logic Simplification PowerPoint Presentation Associative Law In Logic Gates A λ (b λ c) ≡ (a λ b) λ c. For example, there is a logical law corresponding to the associative law of. Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well to addition and multiplication. Some logical operators are associative: A and (b and c) ≡ (a and b). Associative Law In Logic Gates.
From slideplayer.com
Chapter 2 Boolean Algebra and Logic Gate ppt download Associative Law In Logic Gates The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. A λ (b λ c) ≡ (a λ b) λ c. Likewise, the biconditional ↔ is. For. Associative Law In Logic Gates.
From www.nutsvolts.com
Small Logic Gates — The building blocks of versatile digital circuits Associative Law In Logic Gates In this chapter, we will learn about. A and (b and c) ≡ (a and b) and c and in notation, we would write: A λ (b λ c) ≡ (a λ b) λ c. Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. Likewise, the biconditional ↔. Associative Law In Logic Gates.
From www.electronics-lab.com
Logic AND Function Associative Law In Logic Gates A λ (b λ c) ≡ (a λ b) λ c. For example, there is a logical law corresponding to the associative law of. A and (b and c) ≡ (a and b) and c and in notation, we would write: Likewise, the biconditional ↔ is. Many logical laws are similar to algebraic laws. Law of associative states that the. Associative Law In Logic Gates.
From tutorialsinhand.com
Boolean algebra in digital electronics Boolean algebra introduction Associative Law In Logic Gates Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. A and (b and c) ≡ (a and b) and c and in notation, we would write: Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. Some. Associative Law In Logic Gates.
From www.slideserve.com
PPT Logic Gates PowerPoint Presentation, free download ID2999302 Associative Law In Logic Gates Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. In this chapter, we will learn about. A and (b and c) ≡ (a and b) and c and in notation, we would write: Along. Associative Law In Logic Gates.
From hyperelectronic.net
Lesson Logic Gate (OR) HyperElectronic Associative Law In Logic Gates In this chapter, we will learn about. The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. Associative law this law says: Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Each law of the boolean algebra can be interpreted as an operation. Associative Law In Logic Gates.
From www.instructables.com
Basic Logic Gates 7 Steps Instructables Associative Law In Logic Gates Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. Likewise, the biconditional ↔ is. Some logical operators are associative: The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. A and (b and c) ≡ (a. Associative Law In Logic Gates.
From www.slideserve.com
PPT EKT 124 / 3 ELEKTRONIK DIGIT 1 PowerPoint Presentation, free Associative Law In Logic Gates Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. In this chapter, we will learn about. Likewise, the biconditional ↔ is. A λ (b λ c) ≡ (a λ b) λ c. Many logical laws are similar to algebraic laws. Associative law this law says: For example, there. Associative Law In Logic Gates.
From projectiot123.com
Introduction to logic gates Associative Law In Logic Gates The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. A and (b and c) ≡ (a and b) and c and in notation, we would write: Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the.. Associative Law In Logic Gates.
From instrumentationtools.com
Laws of Boolean Algebra using Ladder Logic InstrumentationTools Associative Law In Logic Gates Some logical operators are associative: The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a. Associative Law In Logic Gates.
From wikiblog59.blogspot.com
Logic Gates Diagram And Truth Table / Digital Electronics Logic Gates Associative Law In Logic Gates Likewise, the biconditional ↔ is. A λ (b λ c) ≡ (a λ b) λ c. Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well to addition and multiplication. Both. Associative Law In Logic Gates.
From design.udlvirtual.edu.pe
Classification Of Logic Gates Design Talk Associative Law In Logic Gates A and (b and c) ≡ (a and b) and c and in notation, we would write: Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. In this chapter, we will learn about. Some logical operators are associative: Associative law this law says: Law of associative states that. Associative Law In Logic Gates.
From www.slideserve.com
PPT Basic logic gates PowerPoint Presentation, free download ID3221218 Associative Law In Logic Gates Some logical operators are associative: Associative law this law says: For example, there is a logical law corresponding to the associative law of. Likewise, the biconditional ↔ is. The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. Each law of the boolean algebra can be interpreted as. Associative Law In Logic Gates.
From www.youtube.com
Logic Gates Commutative Associative Distributive Laws Part 3 Associative Law In Logic Gates In this chapter, we will learn about. Likewise, the biconditional ↔ is. The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Many logical laws are similar to algebraic laws. A and (b and. Associative Law In Logic Gates.
From www.youtube.com
Associative Law in electronic circuit Logic Gates Tinker Cad Associative Law In Logic Gates Associative law this law says: Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well to addition and multiplication. In this chapter, we will learn about. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Law of associative states that the order in which the logic operations. Associative Law In Logic Gates.
From www.electronics-lab.com
Logic NAND Function Associative Law In Logic Gates For example, there is a logical law corresponding to the associative law of. A λ (b λ c) ≡ (a λ b) λ c. Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. Many logical laws are similar to algebraic laws. Each law of the boolean algebra can. Associative Law In Logic Gates.
From www.slideserve.com
PPT Chapter 3 Digital Logic Structures PowerPoint Presentation, free Associative Law In Logic Gates A and (b and c) ≡ (a and b) and c and in notation, we would write: Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. Likewise, the biconditional ↔ is. Many logical laws are similar to algebraic laws. Both ∧ and ∨ are associative, as a simple. Associative Law In Logic Gates.
From www.youtube.com
Basic Logic Gates YouTube Associative Law In Logic Gates Many logical laws are similar to algebraic laws. Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. A λ (b λ c) ≡ (a λ b) λ c. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Some logical operators are associative: Along. Associative Law In Logic Gates.
From www.youtube.com
Complete Digital Logic in Hindi video 15 Associative law for all Gates Associative Law In Logic Gates Some logical operators are associative: Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties. Associative Law In Logic Gates.
From www.zeepedia.com
Boolean Addition Multiplication Commutative Law Associative Law Associative Law In Logic Gates The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. Associative law this law says: For example, there is a logical law corresponding to the associative law of. A λ (b λ c) ≡ (a λ b) λ c. Along with the commutative properties of addition and multiplication,. Associative Law In Logic Gates.
From courses.cs.washington.edu
Combinational logic gates Associative Law In Logic Gates Both ∧ and ∨ are associative, as a simple check of truth tables verifies. In this chapter, we will learn about. A and (b and c) ≡ (a and b) and c and in notation, we would write: Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. The. Associative Law In Logic Gates.
From www.slideserve.com
PPT Boolean Algebra & Logic Design PowerPoint Presentation, free Associative Law In Logic Gates Law of associative states that the order in which the logic operations are performed is irrelevant as their effect is the. For example, there is a logical law corresponding to the associative law of. In this chapter, we will learn about. Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a. Associative Law In Logic Gates.
From www.youtube.com
AND LOGIC GATE ? BASICS OF LOGIC GATES ? FUNCTION OF AND GATE ? YouTube Associative Law In Logic Gates A λ (b λ c) ≡ (a λ b) λ c. Associative law this law says: Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well to addition and multiplication. Many logical laws are similar to algebraic laws. Some logical operators are associative: Each law of the boolean algebra can be interpreted. Associative Law In Logic Gates.
From www.etechnog.com
Different Types of Logic Gates with Truth Table, Expression ETechnoG Associative Law In Logic Gates Each law of the boolean algebra can be interpreted as an operation performed by a logic circuit like a logic gate. In this chapter, we will learn about. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. For example, there is a logical law corresponding to the associative law of. A and (b and c). Associative Law In Logic Gates.
From www.slideserve.com
PPT Logic Gates PowerPoint Presentation, free download ID2999302 Associative Law In Logic Gates For example, there is a logical law corresponding to the associative law of. Many logical laws are similar to algebraic laws. In this chapter, we will learn about. Both ∧ and ∨ are associative, as a simple check of truth tables verifies. Along with the commutative properties of addition and multiplication, we have the associative property, again applying equally well. Associative Law In Logic Gates.
From www.storyofmathematics.com
Associative Law Definition & Meaning Associative Law In Logic Gates A λ (b λ c) ≡ (a λ b) λ c. In this chapter, we will learn about. The boolean algebra uses sets of rules for analyzing digital gates and circuits which are known as laws or properties of boolean. A and (b and c) ≡ (a and b) and c and in notation, we would write: Associative law this. Associative Law In Logic Gates.