Standard Basis Of 2X2 Matrix . Then, the set of vectors is called the standard basis of. A 2×2 lower triangular matrix has the form: In this simple presentation, i construct the standard basis in the space of 2x2. You need to show that these form a basis i.e. Here the vector space is 2x2. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. These are linear independent and these span the original set (i.e. A basis for a vector space is by definition a spanning set which is linearly independent. Each set of matrices of the. This is sometimes known as the standard basis. Form a basis for \(\mathbb{r}^n \). The excercise says that this basis must consist of both symmetric and antisymmetric matrices. [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. I have difficulty in that. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2.
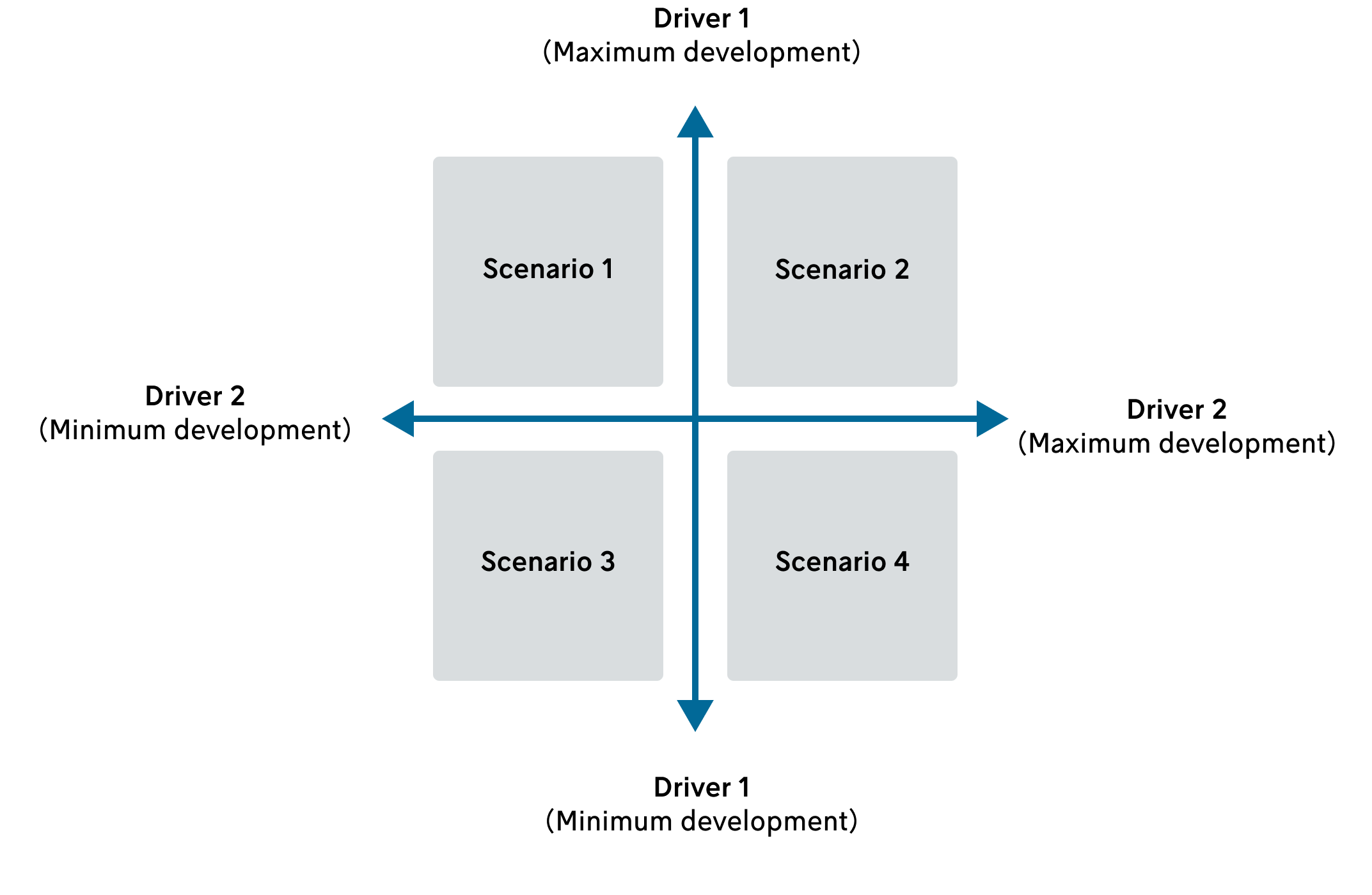
from www.futuresplatform.com
A basis for a vector space is by definition a spanning set which is linearly independent. A 2×2 lower triangular matrix has the form: Here the vector space is 2x2. Each set of matrices of the. These are linear independent and these span the original set (i.e. In particular, \(\mathbb{r}^n \) has dimension \(n\). You need to show that these form a basis i.e. The standard basis is also often. The excercise says that this basis must consist of both symmetric and antisymmetric matrices. Then, the set of vectors is called the standard basis of.
2x2 Scenario Planning Matrix A StepbyStep Guide — Futures Platform
Standard Basis Of 2X2 Matrix | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. A basis for a vector space is by definition a spanning set which is linearly independent. The excercise says that this basis must consist of both symmetric and antisymmetric matrices. Here the vector space is 2x2. In particular, \(\mathbb{r}^n \) has dimension \(n\). [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. Form a basis for \(\mathbb{r}^n \). Each set of matrices of the. These are linear independent and these span the original set (i.e. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. A 2×2 lower triangular matrix has the form: I have difficulty in that. The standard basis is also often. This is sometimes known as the standard basis. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. You need to show that these form a basis i.e.
From www.youtube.com
Linear Algebra Example Problems Change of Coordinates Matrix 2 YouTube Standard Basis Of 2X2 Matrix In this simple presentation, i construct the standard basis in the space of 2x2. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. A 2×2 lower triangular matrix has the form: The excercise says that this basis. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Multiplicación de matrices Producto de matrices 2x2 Ejemplo 2 YouTube Standard Basis Of 2X2 Matrix You need to show that these form a basis i.e. A 2×2 lower triangular matrix has the form: In this simple presentation, i construct the standard basis in the space of 2x2. The standard basis is also often. In particular, \(\mathbb{r}^n \) has dimension \(n\). Form a basis for \(\mathbb{r}^n \). Each set of matrices of the. A basis for. Standard Basis Of 2X2 Matrix.
From www.slideserve.com
PPT Consider the 2x2 matrix PowerPoint Presentation, free download Standard Basis Of 2X2 Matrix | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Form a basis for \(\mathbb{r}^n \). The excercise says that this basis must consist of both symmetric and antisymmetric matrices. The standard basis is also often. Each set of matrices of the. The standard notion of the length of a vector x = (x1, x2,.,. Standard Basis Of 2X2 Matrix.
From www.animalia-life.club
Adding Matrices 2x2 Standard Basis Of 2X2 Matrix This is sometimes known as the standard basis. A basis for a vector space is by definition a spanning set which is linearly independent. These are linear independent and these span the original set (i.e. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. In particular, \(\mathbb{r}^n \) has dimension \(n\). |. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Linear Transformations Projection of X and Y Axis Using 2x2 Matrix Standard Basis Of 2X2 Matrix The standard basis is also often. These are linear independent and these span the original set (i.e. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. A basis for a vector space is by definition a spanning set which is linearly independent. You need to show that these form a basis i.e.. Standard Basis Of 2X2 Matrix.
From www.cuemath.com
Unit Matrix Definition, Properties, Examples Standard Basis Of 2X2 Matrix These are linear independent and these span the original set (i.e. In particular, \(\mathbb{r}^n \) has dimension \(n\). Each set of matrices of the. A 2×2 lower triangular matrix has the form: The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. | | x | | = √x ⋅ x = √(x1)2. Standard Basis Of 2X2 Matrix.
From www.cs.princeton.edu
2x2 Matrices Standard Basis Of 2X2 Matrix A 2×2 lower triangular matrix has the form: In particular, \(\mathbb{r}^n \) has dimension \(n\). Then, the set of vectors is called the standard basis of. Here the vector space is 2x2. In this simple presentation, i construct the standard basis in the space of 2x2. Each set of matrices of the. The excercise says that this basis must consist. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Matrices Multiplication of 2x2 Square Matrices YouTube Standard Basis Of 2X2 Matrix The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. Then, the set of vectors is called the standard basis of. The excercise says that this basis must consist of both symmetric and antisymmetric matrices. In this simple presentation, i construct the standard basis in the space of 2x2. A basis for a. Standard Basis Of 2X2 Matrix.
From www.numerade.com
SOLVED Let W be the set of 2x2 matrices such that A ∈ W is a Standard Basis Of 2X2 Matrix The excercise says that this basis must consist of both symmetric and antisymmetric matrices. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. Each set of matrices of the. The standard basis. Standard Basis Of 2X2 Matrix.
From managementconsulted.com
2x2 Matrix Opposing Characteristics Framework Management Consulted Standard Basis Of 2X2 Matrix Each set of matrices of the. A basis for a vector space is by definition a spanning set which is linearly independent. These are linear independent and these span the original set (i.e. The standard basis is also often. In particular, \(\mathbb{r}^n \) has dimension \(n\). In this simple presentation, i construct the standard basis in the space of 2x2.. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Find a basis for the space of 2 \times 2 diagonal matrices.\text{Basis Standard Basis Of 2X2 Matrix In particular, \(\mathbb{r}^n \) has dimension \(n\). Then, the set of vectors is called the standard basis of. Form a basis for \(\mathbb{r}^n \). I have difficulty in that. [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. The excercise says that this basis must consist of both symmetric. Standard Basis Of 2X2 Matrix.
From www.chegg.com
Solved R2X2 is the space of 2x2 matrices, so that R2X2 is Standard Basis Of 2X2 Matrix Each set of matrices of the. The standard basis is also often. In particular, \(\mathbb{r}^n \) has dimension \(n\). In this simple presentation, i construct the standard basis in the space of 2x2. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. The excercise says that this basis must consist of both. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Matrix with respect to a basis YouTube Standard Basis Of 2X2 Matrix The standard basis is also often. Form a basis for \(\mathbb{r}^n \). The excercise says that this basis must consist of both symmetric and antisymmetric matrices. These are linear independent and these span the original set (i.e. [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. The standard notion. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Tutorial Q78 Basis in vector space of 2x2 matrices YouTube Standard Basis Of 2X2 Matrix The excercise says that this basis must consist of both symmetric and antisymmetric matrices. In particular, \(\mathbb{r}^n \) has dimension \(n\). You need to show that these form a basis i.e. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. A basis for a vector space is by definition a spanning set. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Tutorial Q79 Pauli matrices basis in 2x2 matrices, Part I YouTube Standard Basis Of 2X2 Matrix In particular, \(\mathbb{r}^n \) has dimension \(n\). In this simple presentation, i construct the standard basis in the space of 2x2. A basis for a vector space is by definition a spanning set which is linearly independent. I have difficulty in that. The standard basis is also often. Form a basis for \(\mathbb{r}^n \). The excercise says that this basis. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Linear Algebra check if a 2x2 matrix is diagonalizable YouTube Standard Basis Of 2X2 Matrix A basis for a vector space is by definition a spanning set which is linearly independent. I have difficulty in that. Form a basis for \(\mathbb{r}^n \). In this simple presentation, i construct the standard basis in the space of 2x2. These are linear independent and these span the original set (i.e. This is sometimes known as the standard basis.. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Finding a Standard Matrix Using the Standard Basis YouTube Standard Basis Of 2X2 Matrix A basis for a vector space is by definition a spanning set which is linearly independent. Then, the set of vectors is called the standard basis of. This is sometimes known as the standard basis. In this simple presentation, i construct the standard basis in the space of 2x2. Here the vector space is 2x2. Form a basis for \(\mathbb{r}^n. Standard Basis Of 2X2 Matrix.
From www.numerade.com
SOLVED R2x2 is the space of 2x2 matrices, so that R2x2 is the linear Standard Basis Of 2X2 Matrix Each set of matrices of the. You need to show that these form a basis i.e. The standard basis is also often. The excercise says that this basis must consist of both symmetric and antisymmetric matrices. Form a basis for \(\mathbb{r}^n \). Here the vector space is 2x2. In particular, \(\mathbb{r}^n \) has dimension \(n\). [a 0 c b] where. Standard Basis Of 2X2 Matrix.
From www.youtube.com
4.Eigen values and Basis of eigen space of 2x2 matrix YouTube Standard Basis Of 2X2 Matrix In particular, \(\mathbb{r}^n \) has dimension \(n\). [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. I have difficulty in that. Form a basis for \(\mathbb{r}^n \). These are linear independent and these span the original set (i.e. Then, the set of vectors is called the standard basis of.. Standard Basis Of 2X2 Matrix.
From www.youtube.com
How to calculate determinant of 2x2 matrix by MacSteve tutorials YouTube Standard Basis Of 2X2 Matrix | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Each set of matrices of the. This is sometimes known as the standard basis. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. These are linear independent and these span the original set (i.e. The standard basis. Standard Basis Of 2X2 Matrix.
From www.coursehero.com
[Solved] . Find the coordinate matrix of X relative to the standard Standard Basis Of 2X2 Matrix You need to show that these form a basis i.e. [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. Then, the set of vectors is called the standard basis of. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. In particular,. Standard Basis Of 2X2 Matrix.
From www.researchgate.net
A 2x2 matrix is defined by its columns, image of the basis vectors Standard Basis Of 2X2 Matrix You need to show that these form a basis i.e. Each set of matrices of the. I have difficulty in that. A basis for a vector space is by definition a spanning set which is linearly independent. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. In this simple presentation, i construct. Standard Basis Of 2X2 Matrix.
From www.researchgate.net
Example of a 2x2 scenario matrix. Download Scientific Diagram Standard Basis Of 2X2 Matrix The excercise says that this basis must consist of both symmetric and antisymmetric matrices. A basis for a vector space is by definition a spanning set which is linearly independent. Then, the set of vectors is called the standard basis of. A 2×2 lower triangular matrix has the form: You need to show that these form a basis i.e. In. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Find the eigenvalues and eigenvectors of a 2x2 matrix YouTube Standard Basis Of 2X2 Matrix | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Each set of matrices of the. In this simple presentation, i construct the standard basis in the space of 2x2. The standard basis is also often. You need to show that these form a basis i.e. I have difficulty in that. [a 0 c b]. Standard Basis Of 2X2 Matrix.
From johnathandostie.blogspot.com
Dot Product Of Two 2x2 Matrices Johnathan Dostie's Multiplying Matrices Standard Basis Of 2X2 Matrix Each set of matrices of the. [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. Here the vector space is 2x2. I have difficulty in that. Then, the set of vectors is called the standard basis of. The excercise says that this basis must consist of both symmetric and. Standard Basis Of 2X2 Matrix.
From www.chegg.com
Solved Let V Be The Vector Space Of All 2x2 Upper Triangu... Standard Basis Of 2X2 Matrix The excercise says that this basis must consist of both symmetric and antisymmetric matrices. Here the vector space is 2x2. Then, the set of vectors is called the standard basis of. I have difficulty in that. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. The standard basis is also often. In this simple. Standard Basis Of 2X2 Matrix.
From uxdesign.cc
The 2x2 matrix how to be more systematic about the decisions you make Standard Basis Of 2X2 Matrix Form a basis for \(\mathbb{r}^n \). | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. I have difficulty in that. The excercise says that this basis must consist of both symmetric and antisymmetric matrices. Each set of matrices of the. These are linear independent and these span the original set (i.e. In this simple. Standard Basis Of 2X2 Matrix.
From www.vrogue.co
Matrices Calculating A Linear Map Using A Transformat vrogue.co Standard Basis Of 2X2 Matrix In particular, \(\mathbb{r}^n \) has dimension \(n\). [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. These are linear independent and these span the original set (i.e. I have difficulty in that. Here the. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Eigenvalues and Eigenvectors Example 2x2 Linear Algebra How to Find Standard Basis Of 2X2 Matrix A basis for a vector space is by definition a spanning set which is linearly independent. In this simple presentation, i construct the standard basis in the space of 2x2. Here the vector space is 2x2. Form a basis for \(\mathbb{r}^n \). You need to show that these form a basis i.e. These are linear independent and these span the. Standard Basis Of 2X2 Matrix.
From www.slideserve.com
PPT 2x2 Matrices, Determinants and Inverses PowerPoint Presentation Standard Basis Of 2X2 Matrix In particular, \(\mathbb{r}^n \) has dimension \(n\). The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. The standard basis is also often. In this simple presentation, i construct the standard basis in the space of 2x2. You need to show that these form a basis i.e. A 2×2 lower triangular matrix has. Standard Basis Of 2X2 Matrix.
From www.youtube.com
How to Multiply Matrices A 2x2 Matrix by various sizes YouTube Standard Basis Of 2X2 Matrix The standard basis is also often. Then, the set of vectors is called the standard basis of. The excercise says that this basis must consist of both symmetric and antisymmetric matrices. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. A 2×2 lower triangular matrix has the form: In particular, \(\mathbb{r}^n \) has dimension. Standard Basis Of 2X2 Matrix.
From www.futuresplatform.com
2x2 Scenario Planning Matrix A StepbyStep Guide — Futures Platform Standard Basis Of 2X2 Matrix In particular, \(\mathbb{r}^n \) has dimension \(n\). [a 0 c b] where a, b, and c are elements of a field, such as real numbers or complex. I have difficulty in that. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. This is sometimes known as the standard basis. You need to. Standard Basis Of 2X2 Matrix.
From www.numerade.com
SOLVED (1 point) The set [ ][ ][ ] is called the standard basis Standard Basis Of 2X2 Matrix You need to show that these form a basis i.e. These are linear independent and these span the original set (i.e. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. This is sometimes known as the standard basis. Here the vector space is 2x2. I have difficulty in that. Then, the set of vectors. Standard Basis Of 2X2 Matrix.
From www.youtube.com
Finding a basis for a subset of 2x2 matrices YouTube Standard Basis Of 2X2 Matrix Then, the set of vectors is called the standard basis of. Form a basis for \(\mathbb{r}^n \). Here the vector space is 2x2. This is sometimes known as the standard basis. The standard basis is also often. In this simple presentation, i construct the standard basis in the space of 2x2. The excercise says that this basis must consist of. Standard Basis Of 2X2 Matrix.
From www.chegg.com
Solved 64. Let V be the space of all upper triangular 2x 2 Standard Basis Of 2X2 Matrix The standard basis is also often. A basis for a vector space is by definition a spanning set which is linearly independent. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. Form a basis for \(\mathbb{r}^n \).. Standard Basis Of 2X2 Matrix.