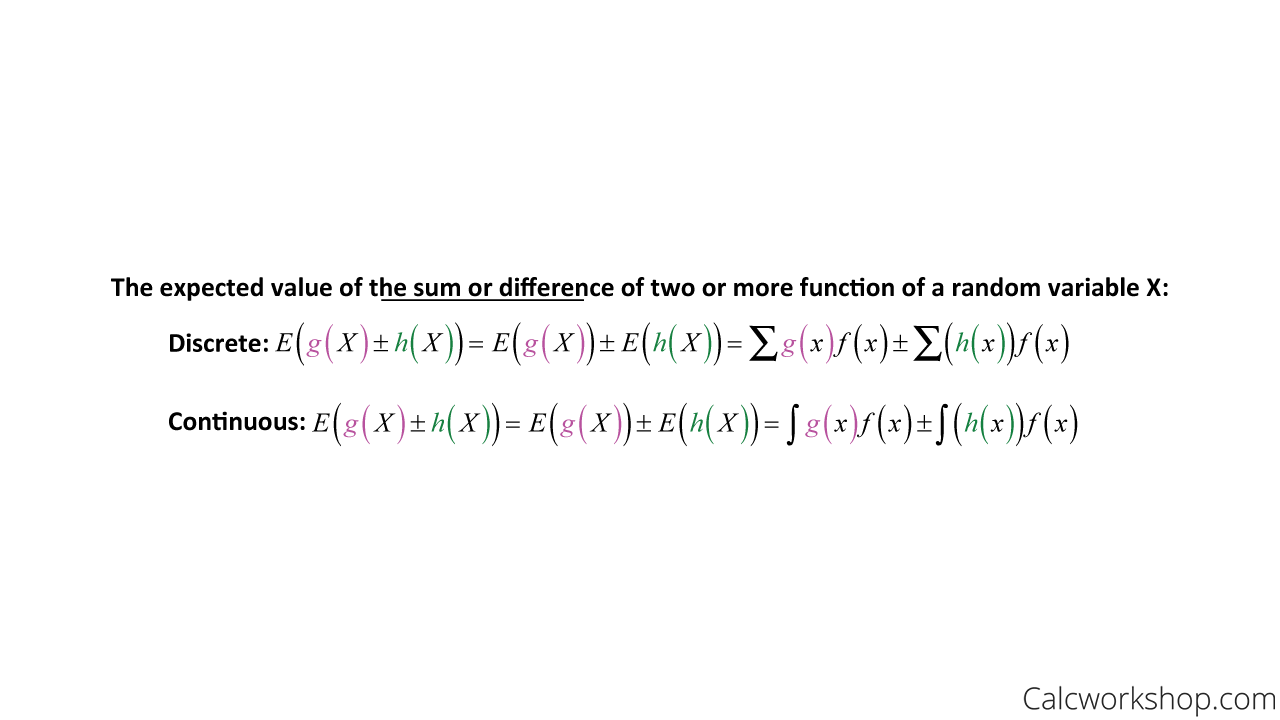Linear Combination Of Poisson Random Variables . an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. • now, consider the random variable. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. this distribution has some other interesting properties relevant to linear combinations. • suppose we have two random variables x and y that have a joint p.d.f. If x 1, x 2,., x n are n independent random variables with respective moment. revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: Firstly, the sum of multiple poisson. is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. Probability & statistics 2 syllabus, written by the. Given by f x,y (x,y). the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of.
from calcworkshop.com
Given by f x,y (x,y). an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. Firstly, the sum of multiple poisson. • now, consider the random variable. If x 1, x 2,., x n are n independent random variables with respective moment. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: • suppose we have two random variables x and y that have a joint p.d.f.
Linear Combination of Random Variables (w/ 9 Examples!)
Linear Combination Of Poisson Random Variables If x 1, x 2,., x n are n independent random variables with respective moment. is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. Probability & statistics 2 syllabus, written by the. revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: • suppose we have two random variables x and y that have a joint p.d.f. If x 1, x 2,., x n are n independent random variables with respective moment. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. this distribution has some other interesting properties relevant to linear combinations. Given by f x,y (x,y). the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. • now, consider the random variable. Firstly, the sum of multiple poisson.
From www.slideserve.com
PPT Lecture 2 PowerPoint Presentation, free download ID2319982 Linear Combination Of Poisson Random Variables this distribution has some other interesting properties relevant to linear combinations. • suppose we have two random variables x and y that have a joint p.d.f. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. Firstly, the sum of multiple poisson. • now, consider the random variable. is there any result. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT Functions of Random Variables PowerPoint Presentation, free Linear Combination Of Poisson Random Variables this distribution has some other interesting properties relevant to linear combinations. Probability & statistics 2 syllabus, written by the. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. Given by f x,y (x,y). If x 1, x 2,., x n are n independent random variables with respective moment. an easy way to. Linear Combination Of Poisson Random Variables.
From www.chegg.com
Solved [25 points] Consider a sequence of Poisson random Linear Combination Of Poisson Random Variables suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. this distribution has some other interesting properties relevant to linear combinations. If x 1, x 2,., x n are n independent random variables with respective moment.. Linear Combination Of Poisson Random Variables.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Of Poisson Random Variables • suppose we have two random variables x and y that have a joint p.d.f. • now, consider the random variable. revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: this distribution has some other interesting properties relevant to linear combinations. Probability & statistics 2 syllabus, written by the. is. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT Functions of Random Variables PowerPoint Presentation, free Linear Combination Of Poisson Random Variables If x 1, x 2,., x n are n independent random variables with respective moment. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. this distribution has some other interesting properties relevant to linear combinations. is there any result about a linear combination of two independent poisson random variables. Linear Combination Of Poisson Random Variables.
From www.studypool.com
SOLUTION Linear Combinations of Random Variables Studypool Linear Combination Of Poisson Random Variables an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. this distribution has some. Linear Combination Of Poisson Random Variables.
From www.youtube.com
Statistics Probability 16 Simple Poisson Random Variable Example YouTube Linear Combination Of Poisson Random Variables suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. this distribution has some. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT Random Variables PowerPoint Presentation, free download ID6390816 Linear Combination Of Poisson Random Variables Given by f x,y (x,y). is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. If x 1, x 2,., x n are n independent random variables with respective moment. Probability & statistics 2 syllabus, written by the. Firstly, the sum of multiple poisson. revision notes on 2.2.1 linear combinations of. Linear Combination Of Poisson Random Variables.
From studylib.net
Linear Combination of Two Random Variables Linear Combination Of Poisson Random Variables revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. Firstly, the sum of multiple poisson. If x 1, x 2,., x n are n independent random variables with respective moment. this distribution has some. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT Math 507, Lecture 8, Fall 2003 PowerPoint Presentation, free Linear Combination Of Poisson Random Variables the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. If x 1, x 2,., x n are n independent random variables with respective moment. • suppose we have two random variables x and y that have a joint p.d.f. • now, consider the random variable. revision notes on 2.2.1. Linear Combination Of Poisson Random Variables.
From www.youtube.com
Calculating values for Poisson Random Variable by Hand Particle Linear Combination Of Poisson Random Variables suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. Probability & statistics 2 syllabus, written by the. • suppose we have two random variables x and y that have a joint p.d.f. revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: is there any result. Linear Combination Of Poisson Random Variables.
From www.postnetwork.co
Poisson Distribution in Statistics Academy Linear Combination Of Poisson Random Variables is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. this. Linear Combination Of Poisson Random Variables.
From www.youtube.com
L23.2 The Sum of Independent Poisson Random Variables YouTube Linear Combination Of Poisson Random Variables revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: Firstly, the sum of multiple poisson. Given by f x,y (x,y). • now, consider the random variable. • suppose we have two random variables x and y that have a joint p.d.f. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables. Linear Combination Of Poisson Random Variables.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Of Poisson Random Variables • suppose we have two random variables x and y that have a joint p.d.f. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. Given by f x,y (x,y). revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: the convolution/sum of probability distributions arises in. Linear Combination Of Poisson Random Variables.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Of Poisson Random Variables Probability & statistics 2 syllabus, written by the. an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. Given by f x,y (x,y). revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: • suppose we have two random variables x. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT 501 Networking Theory & Fundamentals PowerPoint Linear Combination Of Poisson Random Variables an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. this distribution has some other interesting properties relevant to linear combinations. Given by f x,y (x,y). is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. revision notes. Linear Combination Of Poisson Random Variables.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Of Poisson Random Variables • suppose we have two random variables x and y that have a joint p.d.f. If x 1, x 2,., x n are n independent random variables with respective moment. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. Given by f x,y (x,y). Firstly, the sum of multiple poisson.. Linear Combination Of Poisson Random Variables.
From www.youtube.com
Linear Combination of Random Variables YouTube Linear Combination Of Poisson Random Variables is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: If x 1, x 2,., x n are n independent random variables with respective moment. the convolution/sum of probability distributions arises in probability theory and. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT Poisson random variable PowerPoint Presentation, free download Linear Combination Of Poisson Random Variables Given by f x,y (x,y). Probability & statistics 2 syllabus, written by the. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. Firstly, the sum of multiple poisson. • now, consider the random variable. If x 1, x 2,., x n are n independent random variables with respective moment. is. Linear Combination Of Poisson Random Variables.
From www.scribbr.co.uk
Poisson Distributions Definition, Formula & Examples Linear Combination Of Poisson Random Variables • suppose we have two random variables x and y that have a joint p.d.f. Probability & statistics 2 syllabus, written by the. this distribution has some other interesting properties relevant to linear combinations. Given by f x,y (x,y). the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. Firstly,. Linear Combination Of Poisson Random Variables.
From www.postnetwork.co
Poisson Distribution in Statistics Academy Linear Combination Of Poisson Random Variables this distribution has some other interesting properties relevant to linear combinations. If x 1, x 2,., x n are n independent random variables with respective moment. • now, consider the random variable. Given by f x,y (x,y). Firstly, the sum of multiple poisson. an easy way to demonstrate this is by using the property of moment generating functions. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT 501 Networking Theory & Fundamentals PowerPoint Linear Combination Of Poisson Random Variables the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. Firstly, the sum of multiple poisson. this distribution has some other interesting properties relevant to linear combinations. revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: • suppose we have two random variables. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT Poisson random variable PowerPoint Presentation, free download Linear Combination Of Poisson Random Variables is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. If x 1, x 2,., x n are n. Linear Combination Of Poisson Random Variables.
From www.youtube.com
Poisson Random Variable (Probability Distributions) YouTube Linear Combination Of Poisson Random Variables • now, consider the random variable. If x 1, x 2,., x n are n independent random variables with respective moment. is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. Firstly, the sum of multiple poisson. this distribution has some other interesting properties relevant to linear combinations. Given by f. Linear Combination Of Poisson Random Variables.
From www.scribd.com
Additive Properties of Two Independent Poisson Random Variables Linear Combination Of Poisson Random Variables Firstly, the sum of multiple poisson. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. • now, consider the random variable. • suppose we have two random variables. Linear Combination Of Poisson Random Variables.
From www.youtube.com
Linear Combination of Multiple Random Variables Example YouTube Linear Combination Of Poisson Random Variables Given by f x,y (x,y). Firstly, the sum of multiple poisson. If x 1, x 2,., x n are n independent random variables with respective moment. • now, consider the random variable. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. • suppose we have two random variables x and. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT The Poisson Process PowerPoint Presentation, free download ID Linear Combination Of Poisson Random Variables • now, consider the random variable. Probability & statistics 2 syllabus, written by the. this distribution has some other interesting properties relevant to linear combinations. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. If x 1, x 2,., x n are n independent random variables with respective moment. Given. Linear Combination Of Poisson Random Variables.
From www.chegg.com
Solved a. Prove that the sequence of Poisson random Linear Combination Of Poisson Random Variables • now, consider the random variable. an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. If x 1, x 2,., x n are n independent random variables with respective moment. this distribution has some other interesting properties relevant to linear combinations. is there any result. Linear Combination Of Poisson Random Variables.
From www.chegg.com
Solved Show that the sum of independent and identically Linear Combination Of Poisson Random Variables suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. • suppose we have two random variables x and y that have a joint p.d.f. this distribution has some other interesting. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT Poisson random variable PowerPoint Presentation, free download Linear Combination Of Poisson Random Variables is there any result about a linear combination of two independent poisson random variables $a_{1} x_1+a_2 x_2$. an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. revision notes on 2.2.1 linear combinations of random variables for the cie a level maths: Given by f x,y. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT Functions of Random Variables PowerPoint Presentation, free Linear Combination Of Poisson Random Variables Given by f x,y (x,y). an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. revision notes on 2.2.1 linear combinations of random variables for the cie a level. Linear Combination Of Poisson Random Variables.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Of Poisson Random Variables If x 1, x 2,., x n are n independent random variables with respective moment. an easy way to demonstrate this is by using the property of moment generating functions that says for two independent random. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. suppose \(x_1, x_2, \ldots,. Linear Combination Of Poisson Random Variables.
From andymath.com
Poisson Distribution Linear Combination Of Poisson Random Variables this distribution has some other interesting properties relevant to linear combinations. • now, consider the random variable. If x 1, x 2,., x n are n independent random variables with respective moment. Firstly, the sum of multiple poisson. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. an easy way to demonstrate. Linear Combination Of Poisson Random Variables.
From www.slideserve.com
PPT Functions of Random Variables PowerPoint Presentation, free Linear Combination Of Poisson Random Variables suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. Firstly, the sum of multiple poisson. If x 1, x 2,., x n are n independent random variables with respective moment. Probability & statistics 2 syllabus, written by the. revision notes on 2.2.1 linear combinations of random variables for the cie a level maths:. Linear Combination Of Poisson Random Variables.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Of Poisson Random Variables Probability & statistics 2 syllabus, written by the. suppose \(x_1, x_2, \ldots, x_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and. the convolution/sum of probability distributions arises in probability theory and statistics as the operation in terms of. this distribution has some other interesting properties relevant to linear combinations. • now, consider the random variable. . Linear Combination Of Poisson Random Variables.