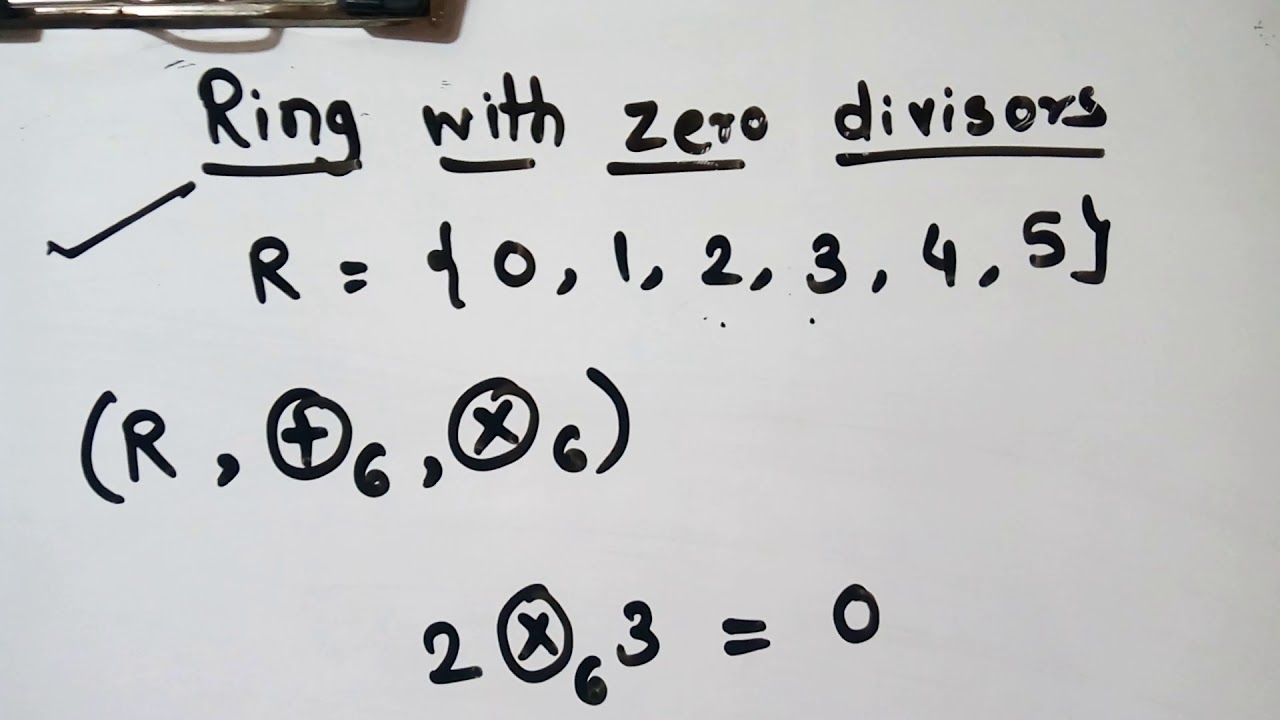Ring Zero Function . +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. The zero ring is a subring of every ring. In the ring \(\left[m_{2\times 2}(\mathbb{r}); A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most.
from www.youtube.com
The zero ring is a subring of every ring. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). In the ring \(\left[m_{2\times 2}(\mathbb{r}); +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,.
Unit 6th Ring with zero divisors and without zero divisors (12) YouTube
Ring Zero Function In the ring \(\left[m_{2\times 2}(\mathbb{r}); A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. In the ring \(\left[m_{2\times 2}(\mathbb{r}); A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. The zero ring is a subring of every ring.
From medium.com
One ring (zero) to rule them all. by Bitst0rm Medium Ring Zero Function A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and. Ring Zero Function.
From www.semanticscholar.org
Figure 2 from Multiplerings filter with dissociated transmission zeros Ring Zero Function +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. In the ring \(\left[m_{2\times 2}(\mathbb{r}); The zero ring is a subring of every ring. A polynomial ring \(r[x]\) over a ring. Ring Zero Function.
From logbar.jp
Ring ZERO by Logbar Ring Zero Function +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). A ring is a set r, together with two. Ring Zero Function.
From www.researchgate.net
Zerodivisor graphs of polynomial rings. Download Scientific Diagram Ring Zero Function A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s).. Ring Zero Function.
From www.pinterest.com
Purchase Engagement Rings Zero's Sims 4 Mods Sims 4 jobs, Sims 4 Ring Zero Function If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. A polynomial ring \(r[x]\). Ring Zero Function.
From www.youtube.com
ring with Zero divisor ring without zero divisor group/ring theory Ring Zero Function If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). In the ring \(\left[m_{2\times 2}(\mathbb{r}); A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in. Ring Zero Function.
From www.artofit.org
What is piston ring function types and uses Artofit Ring Zero Function +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. A ring is. Ring Zero Function.
From xkldase.edu.vn
Details more than 105 ring with zero divisor super hot xkldase.edu.vn Ring Zero Function The zero ring is a subring of every ring. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map. Ring Zero Function.
From xnopytagameing.itch.io
ring_zero by XnopytA, Deathpacitoast Ring Zero Function As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). +, \cdot \right]\) the. Ring Zero Function.
From www.researchgate.net
On the structure of the ring of integervalued entire functions Ring Zero Function A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. The zero ring is a subring of every ring. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails. Ring Zero Function.
From www.techinasia.com
Ring Zero marks a new start for the Japanese wearable Ring Zero Function As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. In the ring \(\left[m_{2\times 2}(\mathbb{r}); +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\. Ring Zero Function.
From www.researchgate.net
The total transmission of a nanoscale AB ring as a function of electron Ring Zero Function If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. The zero. Ring Zero Function.
From www.researchgate.net
Transmission zeros t = 0 and ones t = 1 of the onedimensional ring Ring Zero Function +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. If r and. Ring Zero Function.
From www.youtube.com
Ring Theory Part4(In Bengali)_Units & Some theorems related Unit Ring Zero Function In the ring \(\left[m_{2\times 2}(\mathbb{r}); The zero ring is a subring of every ring. A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. A ring is a set r, together with two. Ring Zero Function.
From www.youtube.com
Abstract Algebra Units and zero divisors of a ring. YouTube Ring Zero Function +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if. Ring Zero Function.
From www.walmart.com
SOFEIYA Violin Cello Making Luthier Tools 11PCS Various Function Ring Zero Function A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. The zero ring is a subring of every ring. If r and s are rings, the. Ring Zero Function.
From www.gizmochina.com
What are Smart Rings? How are they different from other wearables Ring Zero Function A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s).. Ring Zero Function.
From www.youtube.com
Ring with Zero divisor and Without Zero Divisor examples in Hindi Ring Zero Function If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. A polynomial ring \(r[x]\) over a ring \(r\) is. Ring Zero Function.
From www.functionworksheets.com
Characteristics Of Polynomial Functions Worksheet Answer Key Function Ring Zero Function In the ring \(\left[m_{2\times 2}(\mathbb{r}); A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r. Ring Zero Function.
From open.spotify.com
This Is One Ring Zero Spotify Playlist Ring Zero Function The zero ring is a subring of every ring. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z},. Ring Zero Function.
From www.researchgate.net
Singlebus Type I array with five rings Polezero dynamics and the Ring Zero Function If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). The zero ring is a subring of every ring. A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z},. Ring Zero Function.
From exoczxabo.blob.core.windows.net
Function Of The Piston Ring Compressor at James Greene blog Ring Zero Function A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1. Ring Zero Function.
From www.jomashop.com
Bvlgari B.Zero 1 18kt White and Rose Gold 4 Band Ring, Brand Size 54 Ring Zero Function If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). In the ring \(\left[m_{2\times 2}(\mathbb{r}); The zero ring is a subring of every ring. +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0. Ring Zero Function.
From www.youtube.com
Unit 6th Ring with zero divisors and without zero divisors (12) YouTube Ring Zero Function +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. The zero ring is a subring of every ring. If r and s are rings, the zero function from r to s is. Ring Zero Function.
From open.jewelry
OpenJewelry Function Ring Ring Zero Function In the ring \(\left[m_{2\times 2}(\mathbb{r}); The zero ring is a subring of every ring. A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the. Ring Zero Function.
From www.numerade.com
Consider a uniformly charged ring in the xy plane, centered at the Ring Zero Function A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s). +, \cdot. Ring Zero Function.
From www.youtube.com
Ring Without Zero DivisorRing Without Zero Divisor ExampleRing Theory Ring Zero Function +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. If r and. Ring Zero Function.
From www.electricaldesks.com
Difference Between Slip Ring & Split Ring Ring Zero Function The zero ring is a subring of every ring. A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. As with subspaces of vector spaces, it is not hard to check. Ring Zero Function.
From www.youtube.com
Ring Theory 5 Zero Divisors and Integral Domains YouTube Ring Zero Function As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. In the ring \(\left[m_{2\times 2}(\mathbb{r}); If r and s are rings, the zero function from r to s is a ring homomorphism if and only. Ring Zero Function.
From www.youtube.com
A ring R is without zero divisors if and only if the cancellations laws Ring Zero Function A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and. Ring Zero Function.
From www.globalsino.com
(Phase) Contrast Transfer Function (CTF) in CTEM Ring Zero Function A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. In the ring \(\left[m_{2\times 2}(\mathbb{r}); As with subspaces of vector spaces, it is not hard to check that a subset is. Ring Zero Function.
From www.researchgate.net
(PDF) The ring of entire functions Ring Zero Function A polynomial ring \(r[x]\) over a ring \(r\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{z}, n\geq 0, a_i \in r, \forall i=1,. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. In the ring. Ring Zero Function.
From www.ebay.com
O ring zero ring 5.23 X 2.62 Viton FPM FKM 80 shore quantity 2/10/25/50 Ring Zero Function A ring is a set r, together with two binary opera tions addition and multiplication, denoted + and · respectively, which satisfy the following. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1 s).. Ring Zero Function.
From www.walmart.com
Hand Grip Ring Multifunctional Senior Forearm Exerciser and Ring Zero Function In the ring \(\left[m_{2\times 2}(\mathbb{r}); As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. If r and s are rings, the zero function from r to s is a ring homomorphism if and only if s is the zero ring (otherwise it fails to map 1 r to 1. Ring Zero Function.
From www.researchgate.net
Simulation of the (a) input Gaussian beam, (b) LaguerreGauss beam Ring Zero Function The zero ring is a subring of every ring. +, \cdot \right]\) the matrices \(a=\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\. As with subspaces of vector spaces, it is not hard to check that a subset is a subring as most. In the ring \(\left[m_{2\times 2}(\mathbb{r}); A ring is a set r, together with two binary opera. Ring Zero Function.