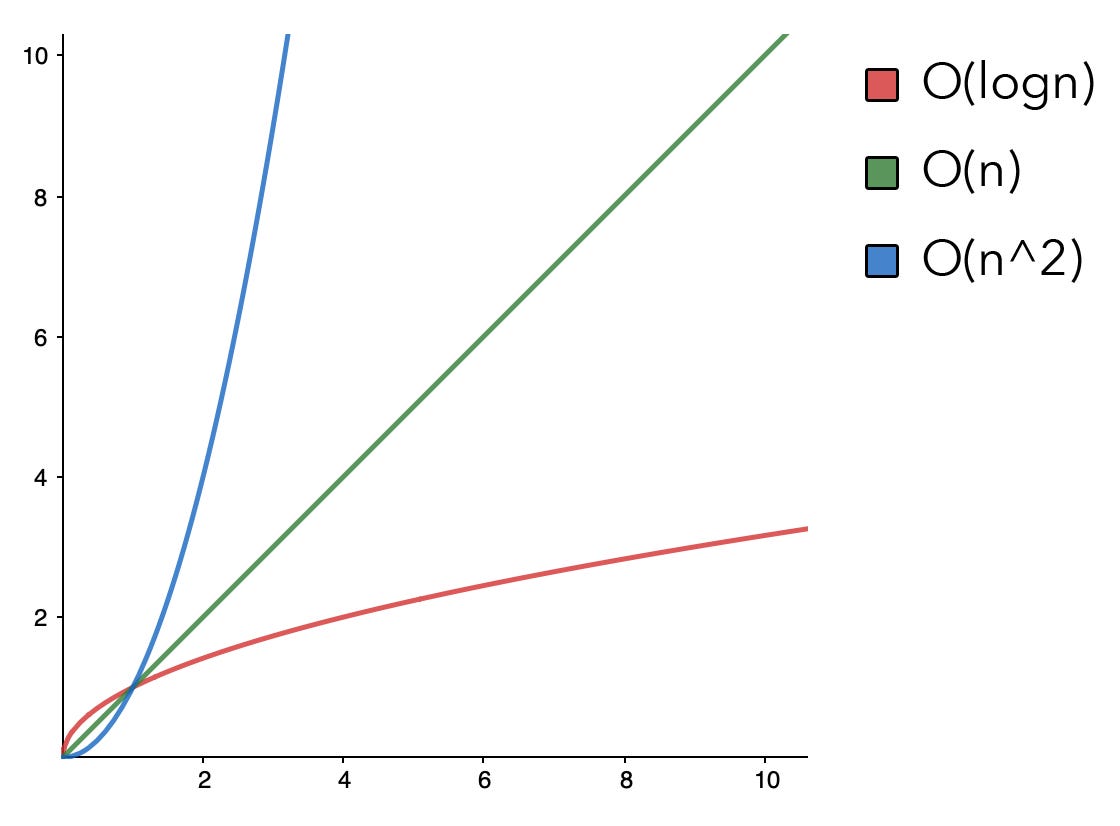
Is N Log N Greater Than N at Kiara Cann blog

Is N Log N Greater Than N. If we assume n ≥ 1 n ≥ 1, we have log n ≥ 1 log n ≥ 1. Logarithmic time complexity is denoted as o(log n). O(1) means the running time of an algorithm is independent of the input size and is bounded by. When using data structures, if one more element is needed every time n increases by one, then the algorithm will use o (n) space. $\log n$ is the inverse of $2^n$. O (nlogn) is known as loglinear complexity. With that we have log2. To understand this let us. It is a measure of how the runtime of an algorithm scales as the input size. Just as $2^n$ grows faster than any polynomial $n^k$ regardless of how large a finite $k$ is, $\log n$ will grow slower than any polynomial functions $n^k$. Yes, there is a huge difference. To demonstrate with a counterexample, let $f(n) = 10^{100} \log n$ (an $o(\log n)$ algorithm; Is o(1) always faster than o(log n)? Regarding your follow up question: Thus, binary search o(log(n)) and heapsort o(n log(n)) are efficient algorithms, while linear search o(n) and bubblesort o(n²).

Yes, there is a huge difference. When using data structures, if one more element is needed every time n increases by one, then the algorithm will use o (n) space. One thing to understand about n*log (n) is that it is relatively close to a linear complexity of o (n). With that we have log2. O (nlogn) is known as loglinear complexity. $\log n$ is the inverse of $2^n$. It is a measure of how the runtime of an algorithm scales as the input size. To understand this let us. O(1) means the running time of an algorithm is independent of the input size and is bounded by. Regarding your follow up question:

What is O(n)? — Big O Notation + How to use it by Timo Makhlay Medium

Is N Log N Greater Than N O (nlogn) is known as loglinear complexity. Logarithmic time complexity is denoted as o(log n). Is o(1) always faster than o(log n)? O (nlogn) is known as loglinear complexity. With that we have log2. To understand this let us. If we assume n ≥ 1 n ≥ 1, we have log n ≥ 1 log n ≥ 1. Regarding your follow up question: One thing to understand about n*log (n) is that it is relatively close to a linear complexity of o (n). O(1) means the running time of an algorithm is independent of the input size and is bounded by. Thus, binary search o(log(n)) and heapsort o(n log(n)) are efficient algorithms, while linear search o(n) and bubblesort o(n²). Just as $2^n$ grows faster than any polynomial $n^k$ regardless of how large a finite $k$ is, $\log n$ will grow slower than any polynomial functions $n^k$. To demonstrate with a counterexample, let $f(n) = 10^{100} \log n$ (an $o(\log n)$ algorithm; It is a measure of how the runtime of an algorithm scales as the input size. Yes, there is a huge difference. $\log n$ is the inverse of $2^n$.