Cone Path Equation . In this chapter i will discuss what the intersection of a plane with a right circular cone looks like. If the plane is parallel to the axis of revolution (the y. a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; The three types are parabolas, ellipses, and hyperbolas. Ax 2 + bxy + cy 2 + dx + ey + f = 0 from that equation we can create. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. Sometimes it is useful to write or identify the equation of a conic section in polar form. plane sections of a cone. polar equations of conic sections. conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone. give each one a factor (a,b,c etc) and we get a general equation that covers all conic sections:
from exoglrmwh.blob.core.windows.net
a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; The three types are parabolas, ellipses, and hyperbolas. In this chapter i will discuss what the intersection of a plane with a right circular cone looks like. Sometimes it is useful to write or identify the equation of a conic section in polar form. give each one a factor (a,b,c etc) and we get a general equation that covers all conic sections: plane sections of a cone. conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone. Ax 2 + bxy + cy 2 + dx + ey + f = 0 from that equation we can create. polar equations of conic sections.
Equation Of A Cone at Margaret Carle blog
Cone Path Equation polar equations of conic sections. give each one a factor (a,b,c etc) and we get a general equation that covers all conic sections: The three types are parabolas, ellipses, and hyperbolas. polar equations of conic sections. conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). In this chapter i will discuss what the intersection of a plane with a right circular cone looks like. Sometimes it is useful to write or identify the equation of a conic section in polar form. plane sections of a cone. Ax 2 + bxy + cy 2 + dx + ey + f = 0 from that equation we can create. a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. If the plane is parallel to the axis of revolution (the y.
From www.youtube.com
Cone in 3D geometry,Equation of cone with vertex on origin YouTube Cone Path Equation give each one a factor (a,b,c etc) and we get a general equation that covers all conic sections: plane sections of a cone. polar equations of conic sections. Sometimes it is useful to write or identify the equation of a conic section in polar form. $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know. Cone Path Equation.
From www.youtube.com
Cone Volume Formula Math Animation YouTube Cone Path Equation a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. The three types are parabolas, ellipses, and hyperbolas. conic sections. Cone Path Equation.
From www.cuemath.com
Frustum of Cone Formula, Properties, Definition, Examples Cone Path Equation plane sections of a cone. The three types are parabolas, ellipses, and hyperbolas. If the plane is parallel to the axis of revolution (the y. Sometimes it is useful to write or identify the equation of a conic section in polar form. a conic section (or simply conic) is a curve obtained as the intersection of the surface. Cone Path Equation.
From www.cuemath.com
Volume of a Cone with Diameter Formula, Definition, Examples Cone Path Equation one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. give each one a factor (a,b,c etc) and we get a general equation that covers all conic sections: Sometimes it is useful to write or identify the equation of a conic section in. Cone Path Equation.
From donsteward.blogspot.co.uk
MEDIAN Don Steward mathematics teaching cone surface area Cone Path Equation plane sections of a cone. If the plane is parallel to the axis of revolution (the y. Sometimes it is useful to write or identify the equation of a conic section in polar form. The three types are parabolas, ellipses, and hyperbolas. conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex. Cone Path Equation.
From www.cuemath.com
What is Cone Formula, Properties, Examples Cuemath Cone Path Equation Sometimes it is useful to write or identify the equation of a conic section in polar form. Ax 2 + bxy + cy 2 + dx + ey + f = 0 from that equation we can create. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law. Cone Path Equation.
From www.dreamstime.com
Right Circular Cone Formula. Shape in Mathematics. Inscribed with Cone Path Equation If the plane is parallel to the axis of revolution (the y. plane sections of a cone. In this chapter i will discuss what the intersection of a plane with a right circular cone looks like. conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). a conic section (or. Cone Path Equation.
From www.cuemath.com
Right Circular Cone Formula, Properties, Definition, Examples Cone Path Equation conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone. a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone. Cone Path Equation.
From www.adda247.com
Surface Area of a Cone Formula, Derivation, Examples Cone Path Equation The three types are parabolas, ellipses, and hyperbolas. plane sections of a cone. give each one a factor (a,b,c etc) and we get a general equation that covers all conic sections: Sometimes it is useful to write or identify the equation of a conic section in polar form. a conic section (or simply conic) is a curve. Cone Path Equation.
From exoeboqyu.blob.core.windows.net
Cone Axis Function at Charles Bergin blog Cone Path Equation conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). give each one a factor (a,b,c etc) and we get a general equation that covers all conic sections: Sometimes it is useful to write or identify the equation of a conic section in polar form. polar equations of conic sections.. Cone Path Equation.
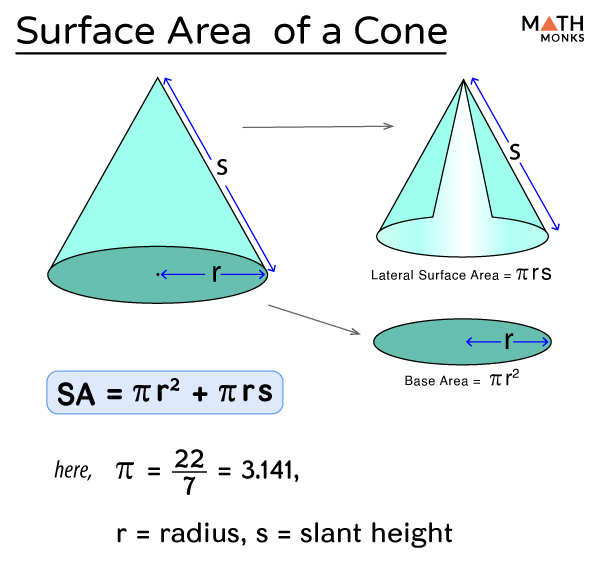
From mathmonks.com
Surface Area of Cone Formula, Examples, and Diagrams Cone Path Equation plane sections of a cone. Sometimes it is useful to write or identify the equation of a conic section in polar form. polar equations of conic sections. a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; The three types are parabolas, ellipses, and hyperbolas.. Cone Path Equation.
From dxogtjzao.blob.core.windows.net
Cone Volume Equation Calculator at Christine Funk blog Cone Path Equation plane sections of a cone. The three types are parabolas, ellipses, and hyperbolas. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. If the plane is parallel to the axis of revolution (the y. Ax 2 + bxy + cy 2 +. Cone Path Equation.
From www.dreamstime.com
Area and Volume of the Rotating Cone Stock Illustration Illustration Cone Path Equation polar equations of conic sections. In this chapter i will discuss what the intersection of a plane with a right circular cone looks like. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. give each one a factor (a,b,c etc) and. Cone Path Equation.
From www.slideserve.com
PPT TOPIC CONE PowerPoint Presentation, free download ID6246849 Cone Path Equation one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. plane sections of a cone. conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). In this chapter i will discuss what the intersection of. Cone Path Equation.
From www.chegg.com
Solved (1) Find the geodesic (the shortest path between two Cone Path Equation Ax 2 + bxy + cy 2 + dx + ey + f = 0 from that equation we can create. a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path. Cone Path Equation.
From bazabriancoleman.blogspot.com
Total Surface Area of Cone Brian Coleman Cone Path Equation The three types are parabolas, ellipses, and hyperbolas. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. polar equations of conic sections. plane sections of a cone. a conic section (or simply conic) is a curve obtained as the intersection. Cone Path Equation.
From www.mathcation.com
The Easy Formula for How to Find the Volume of a Cone Mathcation Cone Path Equation Ax 2 + bxy + cy 2 + dx + ey + f = 0 from that equation we can create. plane sections of a cone. a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; give each one a factor (a,b,c etc) and we. Cone Path Equation.
From cookinglove.com
Surface area of a cone formula explained Cone Path Equation plane sections of a cone. Sometimes it is useful to write or identify the equation of a conic section in polar form. The three types are parabolas, ellipses, and hyperbolas. give each one a factor (a,b,c etc) and we get a general equation that covers all conic sections: Ax 2 + bxy + cy 2 + dx +. Cone Path Equation.
From cookinglove.com
Surface area of a cone formula explained Cone Path Equation one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. The three types are parabolas, ellipses, and hyperbolas. In this chapter i will discuss what the intersection of a plane with a right circular cone looks like. a conic section (or simply conic). Cone Path Equation.
From www.youtube.com
Cones. How To Find The Height Of A Cone Given Its Volume And Radius Cone Path Equation one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. In this chapter i will discuss what the intersection of a plane with a right circular cone looks like. polar equations of conic sections. a conic section (or simply conic) is a. Cone Path Equation.
From exoglrmwh.blob.core.windows.net
Equation Of A Cone at Margaret Carle blog Cone Path Equation If the plane is parallel to the axis of revolution (the y. Sometimes it is useful to write or identify the equation of a conic section in polar form. polar equations of conic sections. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a. Cone Path Equation.
From topptutors.blogspot.com
How To Find The Height Of A Cone Formula Cone Path Equation $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone. conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). polar equations of conic sections. Sometimes it is useful to write or identify the equation of a conic section. Cone Path Equation.
From cookinglove.com
Surface area of a cone formula explained Cone Path Equation plane sections of a cone. a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; Sometimes it is useful to write or identify the equation of a conic section in polar form. one application is that a moving particle that is subjected to an inverse. Cone Path Equation.
From exomybxri.blob.core.windows.net
Cone Equation Calc 3 at Christine Mireles blog Cone Path Equation $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone. Sometimes it is useful to write or identify the equation of a conic section in polar form. polar equations of conic sections. If the plane is parallel to the axis of revolution (the y. In this chapter. Cone Path Equation.
From www.cuemath.com
Base Area of a Cone Definition, Formula and Examples Cone Path Equation If the plane is parallel to the axis of revolution (the y. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone.. Cone Path Equation.
From www.slideserve.com
PPT TOPIC CONE PowerPoint Presentation, free download ID6246849 Cone Path Equation one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. If the plane is parallel to the axis of revolution (the y. $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone.. Cone Path Equation.
From cookinglove.com
Surface area of a cone formula explained Cone Path Equation Ax 2 + bxy + cy 2 + dx + ey + f = 0 from that equation we can create. If the plane is parallel to the axis of revolution (the y. polar equations of conic sections. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's. Cone Path Equation.
From www.toppr.com
A hollow right circular cone is fixed with its axis vertical and vertex Cone Path Equation The three types are parabolas, ellipses, and hyperbolas. Sometimes it is useful to write or identify the equation of a conic section in polar form. one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is. Cone Path Equation.
From cookinglove.com
Surface area of a cone formula explained Cone Path Equation If the plane is parallel to the axis of revolution (the y. Ax 2 + bxy + cy 2 + dx + ey + f = 0 from that equation we can create. conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). give each one a factor (a,b,c etc) and. Cone Path Equation.
From www.youtube.com
How to find the Volume of a Cone Mathcation YouTube Cone Path Equation one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone. give each one a factor (a,b,c etc) and we get a. Cone Path Equation.
From www.pw.live
Cone Formula Equation And Examples Cone Path Equation one application is that a moving particle that is subjected to an inverse square law force like gravity or coulomb's law will follow a path. a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; Ax 2 + bxy + cy 2 + dx + ey. Cone Path Equation.
From www.youtube.com
Vector Equation of the Curve of Intersection of a Hemisphere and Cone Cone Path Equation If the plane is parallel to the axis of revolution (the y. a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane; polar equations of conic sections. $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line. Cone Path Equation.
From ar.inspiredpencil.com
Equation Of A 3d Cone Cone Path Equation conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). In this chapter i will discuss what the intersection of a plane with a right circular cone looks like. plane sections of a cone. Sometimes it is useful to write or identify the equation of a conic section in polar form.. Cone Path Equation.
From www.youtube.com
4d. Volume of a cone as a triple integral in spherical coordinates Cone Path Equation Sometimes it is useful to write or identify the equation of a conic section in polar form. $a= (x_1,y_1,z_1)$ and $b=(x_2,y_2,z_2)$ and cone equation is $x^2+y^2=r^2z^2$ i know that the shortest path is a line on the cone. Ax 2 + bxy + cy 2 + dx + ey + f = 0 from that equation we can create.. Cone Path Equation.
From www.cuemath.com
Right Circular Cone Formula, Properties, Definition, Examples Cone Path Equation In this chapter i will discuss what the intersection of a plane with a right circular cone looks like. polar equations of conic sections. Sometimes it is useful to write or identify the equation of a conic section in polar form. one application is that a moving particle that is subjected to an inverse square law force like. Cone Path Equation.