Orthogonal Matrix Solved Problems . What kinds of matrices interact well with this notion of distance? But why the name orthogonal for it? Example of 2×2 orthogonal matrix. (b) find a 2£2 matrix a such that deta = 1, but also such. Orthogonal matrices are also characterized by the following theorem. Let us look into the definition of the. (a) suppose that a is an orthogonal matrix. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: Prove that either deta = 1 or deta = ¡1. If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of the matrix, the matrix is said to be orthogonal. But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. Work the problems on your own and check your answers when you’re done. Suppose that a is an n n matrix. Orthogonal matrices are those preserving the dot product. This section provides a lesson on.
from www.chegg.com
Work the problems on your own and check your answers when you’re done. But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. Let us look into the definition of the. Suppose that a is an n n matrix. (a) suppose that a is an orthogonal matrix. But why the name orthogonal for it? What kinds of matrices interact well with this notion of distance? (b) find a 2£2 matrix a such that deta = 1, but also such. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: Orthogonal matrices are those preserving the dot product.
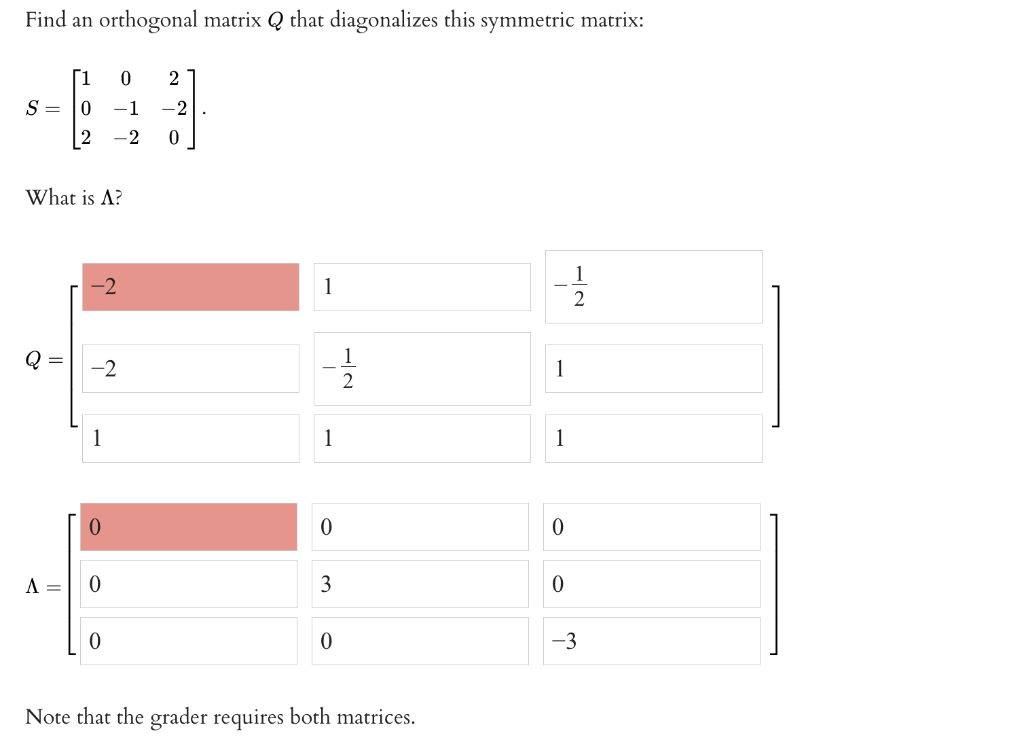
Solved Find an orthogonal matrix Q that diagonalizes this
Orthogonal Matrix Solved Problems Let us look into the definition of the. This section provides a lesson on. But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. (a) suppose that a is an orthogonal matrix. Prove that either deta = 1 or deta = ¡1. Let us look into the definition of the. Orthogonal matrices are those preserving the dot product. What kinds of matrices interact well with this notion of distance? (b) find a 2£2 matrix a such that deta = 1, but also such. Suppose that a is an n n matrix. Orthogonal matrices are also characterized by the following theorem. But why the name orthogonal for it? Work the problems on your own and check your answers when you’re done. If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of the matrix, the matrix is said to be orthogonal. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: Example of 2×2 orthogonal matrix.
From www.numerade.com
SOLVED Read 'Orthonormal Bases and Complements Relating Orthonormal Orthogonal Matrix Solved Problems (a) suppose that a is an orthogonal matrix. But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. Orthogonal matrices are those preserving the dot product. But why the name orthogonal for it? (b) find a 2£2 matrix a such that deta = 1, but also such.. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Problem 25 Which of the following orthogonal matrix Orthogonal Matrix Solved Problems Suppose that a is an n n matrix. (a) suppose that a is an orthogonal matrix. Example of 2×2 orthogonal matrix. (b) find a 2£2 matrix a such that deta = 1, but also such. This section provides a lesson on. What kinds of matrices interact well with this notion of distance? Orthogonal matrices are those preserving the dot product.. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved 5. Find an orthogonal matrix Q and a diagonal matrix Orthogonal Matrix Solved Problems (b) find a 2£2 matrix a such that deta = 1, but also such. Example of 2×2 orthogonal matrix. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of the matrix, the. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved If A is a real 3x3 matrix with det (A) = 1, find det Orthogonal Matrix Solved Problems If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of the matrix, the matrix is said to be orthogonal. (a) suppose that a is an orthogonal matrix. Work the problems on your own and check your answers when you’re done. What kinds of matrices interact well with this notion of distance?. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Consider an orthogonal m times n matrix. Q, and think Orthogonal Matrix Solved Problems Orthogonal matrices are also characterized by the following theorem. (b) find a 2£2 matrix a such that deta = 1, but also such. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: Example of 2×2 orthogonal matrix. Prove that either deta = 1 or deta = ¡1. Let us look. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved aim of this problem is to review orthonormal bases Orthogonal Matrix Solved Problems Prove that either deta = 1 or deta = ¡1. Suppose that a is an n n matrix. But why the name orthogonal for it? Orthogonal matrices are also characterized by the following theorem. This section provides a lesson on. (b) find a 2£2 matrix a such that deta = 1, but also such. What kinds of matrices interact well. Orthogonal Matrix Solved Problems.
From www.coursehero.com
[Solved] . A is an orthogonal matrix given by a b C A = d e f g h i Orthogonal Matrix Solved Problems Let us look into the definition of the. This section provides a lesson on. Example of 2×2 orthogonal matrix. (b) find a 2£2 matrix a such that deta = 1, but also such. (a) suppose that a is an orthogonal matrix. If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved The inverse of the orthogonal matrix A=[53545−453] Orthogonal Matrix Solved Problems Suppose that a is an n n matrix. (b) find a 2£2 matrix a such that deta = 1, but also such. Orthogonal matrices are also characterized by the following theorem. Let us look into the definition of the. Example of 2×2 orthogonal matrix. Prove that either deta = 1 or deta = ¡1. This section provides a lesson on.. Orthogonal Matrix Solved Problems.
From www.numerade.com
SOLVED Find an orthonormal bagis for the column space; col(A), of the Orthogonal Matrix Solved Problems But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. What kinds of matrices interact well with this notion of distance? Orthogonal matrices are those preserving the dot product. Let us look into the definition of the. Orthogonal matrices are also characterized by the following theorem. (a). Orthogonal Matrix Solved Problems.
From www.youtube.com
Orthogonal Matrix & solved problem for BBA,BCA part04 by Prof Orthogonal Matrix Solved Problems Suppose that a is an n n matrix. Work the problems on your own and check your answers when you’re done. Let us look into the definition of the. (a) suppose that a is an orthogonal matrix. But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix.. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Orthogonally diagonalize the matrix below, giving an Orthogonal Matrix Solved Problems But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. Example of 2×2 orthogonal matrix. This section provides a lesson on. Prove that either deta = 1 or deta = ¡1. Orthogonal matrices are those preserving the dot product. Orthogonal matrices are also characterized by the following. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved a. Which of the matrices are orthogonal (has Orthogonal Matrix Solved Problems Suppose that a is an n n matrix. (b) find a 2£2 matrix a such that deta = 1, but also such. But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. Prove that either deta = 1 or deta = ¡1. What kinds of matrices interact. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved 12. Recall that an orthogonal matrix is a square Orthogonal Matrix Solved Problems Example of 2×2 orthogonal matrix. Let us look into the definition of the. But why the name orthogonal for it? Suppose that a is an n n matrix. (b) find a 2£2 matrix a such that deta = 1, but also such. Work the problems on your own and check your answers when you’re done. This section provides a lesson. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved For each given matrix A, find orthonormal basis for Orthogonal Matrix Solved Problems But why the name orthogonal for it? Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: Prove that either deta = 1 or deta = ¡1. (b) find a 2£2 matrix a such that deta = 1, but also such. Suppose that a is an n n matrix. But if. Orthogonal Matrix Solved Problems.
From www.numerade.com
SOLVED Orthogonal Transformations Orthogonal Matrices In Exercises 12 Orthogonal Matrix Solved Problems Let us look into the definition of the. (a) suppose that a is an orthogonal matrix. Orthogonal matrices are also characterized by the following theorem. This section provides a lesson on. But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. Work the problems on your own. Orthogonal Matrix Solved Problems.
From www.coursehero.com
[Solved] 22 10 107 Let A = 10 7 20 . Find an orthogonal matrix P with Orthogonal Matrix Solved Problems Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: Work the problems on your own and check your answers when you’re done. What kinds of matrices interact well with this notion of distance? If the transpose of a square matrix with real numbers or values is equal to the inverse. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Problem 12 Practice with Orthogonal Matrices Consider Orthogonal Matrix Solved Problems Let us look into the definition of the. What kinds of matrices interact well with this notion of distance? Suppose that a is an n n matrix. Orthogonal matrices are those preserving the dot product. (b) find a 2£2 matrix a such that deta = 1, but also such. Work the problems on your own and check your answers when. Orthogonal Matrix Solved Problems.
From www.numerade.com
Orthogonally diagonalize the matrices in Exercises 1322, giving an Orthogonal Matrix Solved Problems Suppose that a is an n n matrix. Let us look into the definition of the. If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of the matrix, the matrix is said to be orthogonal. Orthogonal matrices are also characterized by the following theorem. Example of 2×2 orthogonal matrix. Work the. Orthogonal Matrix Solved Problems.
From www.studypool.com
SOLUTION Symmetric skew symmetric matrices idea and solved examples Orthogonal Matrix Solved Problems Let us look into the definition of the. (b) find a 2£2 matrix a such that deta = 1, but also such. Work the problems on your own and check your answers when you’re done. Orthogonal matrices are those preserving the dot product. (a) suppose that a is an orthogonal matrix. Matrices with orthonormal columns are a new class of. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Find orthogonal matrix of following matrix. (hint if Orthogonal Matrix Solved Problems (a) suppose that a is an orthogonal matrix. Suppose that a is an n n matrix. Orthogonal matrices are those preserving the dot product. But why the name orthogonal for it? Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: Orthogonal matrices are also characterized by the following theorem. This. Orthogonal Matrix Solved Problems.
From www.numerade.com
SOLVED Problem 5 Show that an orthogonal triangular matrix is a Orthogonal Matrix Solved Problems Prove that either deta = 1 or deta = ¡1. What kinds of matrices interact well with this notion of distance? (b) find a 2£2 matrix a such that deta = 1, but also such. Example of 2×2 orthogonal matrix. If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of the. Orthogonal Matrix Solved Problems.
From www.youtube.com
Orthonormal,Orthogonal matrix (EE MATH มทส.) YouTube Orthogonal Matrix Solved Problems Orthogonal matrices are those preserving the dot product. Work the problems on your own and check your answers when you’re done. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: This section provides a lesson on. Orthogonal matrices are also characterized by the following theorem. But if the transpose of. Orthogonal Matrix Solved Problems.
From www.numerade.com
SOLVED In each of Problems 18, find the eigenvalues and cor Orthogonal Matrix Solved Problems But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. Prove that either deta = 1 or deta = ¡1. (b) find a 2£2 matrix a such that deta = 1, but also such. Suppose that a is an n n matrix. (a) suppose that a is. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Problem 8. (20 pts) Let Find an orthogonal matrix Q Orthogonal Matrix Solved Problems (b) find a 2£2 matrix a such that deta = 1, but also such. Orthogonal matrices are those preserving the dot product. This section provides a lesson on. Work the problems on your own and check your answers when you’re done. Suppose that a is an n n matrix. Orthogonal matrices are also characterized by the following theorem. Matrices with. Orthogonal Matrix Solved Problems.
From www.numerade.com
SOLVEDStatement 1 and Statement 2 Determinant of an orthogonal matrix Orthogonal Matrix Solved Problems Example of 2×2 orthogonal matrix. (b) find a 2£2 matrix a such that deta = 1, but also such. Orthogonal matrices are those preserving the dot product. But why the name orthogonal for it? What kinds of matrices interact well with this notion of distance? This section provides a lesson on. Suppose that a is an n n matrix. But. Orthogonal Matrix Solved Problems.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Orthogonal Matrix Solved Problems But why the name orthogonal for it? (a) suppose that a is an orthogonal matrix. Prove that either deta = 1 or deta = ¡1. Orthogonal matrices are also characterized by the following theorem. Example of 2×2 orthogonal matrix. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: What kinds. Orthogonal Matrix Solved Problems.
From www.docsity.com
2 Solved Problems on Orthogonal Matrix Quiz 11 MATH 1502 Docsity Orthogonal Matrix Solved Problems (b) find a 2£2 matrix a such that deta = 1, but also such. What kinds of matrices interact well with this notion of distance? Orthogonal matrices are those preserving the dot product. Work the problems on your own and check your answers when you’re done. Orthogonal matrices are also characterized by the following theorem. Prove that either deta =. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Let A = .Note Note that the columns of A are Orthogonal Matrix Solved Problems Prove that either deta = 1 or deta = ¡1. (b) find a 2£2 matrix a such that deta = 1, but also such. But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. Let us look into the definition of the. Work the problems on your. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Proceed as in this example to construct an orthogonal Orthogonal Matrix Solved Problems Orthogonal matrices are those preserving the dot product. (a) suppose that a is an orthogonal matrix. Example of 2×2 orthogonal matrix. But why the name orthogonal for it? Work the problems on your own and check your answers when you’re done. Orthogonal matrices are also characterized by the following theorem. Suppose that a is an n n matrix. (b) find. Orthogonal Matrix Solved Problems.
From www.coursehero.com
[Solved] . Fill in the missing values to make an orthogonal matrix. i Orthogonal Matrix Solved Problems But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. Prove that either deta = 1 or deta = ¡1. (a) suppose that a is an orthogonal matrix. What kinds of matrices interact well with this notion of distance? Suppose that a is an n n matrix.. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Find an orthogonal matrix Q that diagonalizes this Orthogonal Matrix Solved Problems Orthogonal matrices are also characterized by the following theorem. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: Example of 2×2 orthogonal matrix. If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of the matrix, the matrix is said to be. Orthogonal Matrix Solved Problems.
From www.coursehero.com
[Solved] . Find an orthogonal basis for the column space of the matrix Orthogonal Matrix Solved Problems Orthogonal matrices are those preserving the dot product. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: Let us look into the definition of the. Work the problems on your own and check your answers when you’re done. (b) find a 2£2 matrix a such that deta = 1, but. Orthogonal Matrix Solved Problems.
From www.chegg.com
Solved Let A = . Note that the columns of A are orthonormal Orthogonal Matrix Solved Problems Orthogonal matrices are those preserving the dot product. Prove that either deta = 1 or deta = ¡1. (a) suppose that a is an orthogonal matrix. Example of 2×2 orthogonal matrix. This section provides a lesson on. If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of the matrix, the matrix. Orthogonal Matrix Solved Problems.
From www.youtube.com
Trick to find Inverse of (A.A^T) of Orthogonal Matrix GATE question Orthogonal Matrix Solved Problems What kinds of matrices interact well with this notion of distance? Let us look into the definition of the. Work the problems on your own and check your answers when you’re done. Prove that either deta = 1 or deta = ¡1. Suppose that a is an n n matrix. This section provides a lesson on. Example of 2×2 orthogonal. Orthogonal Matrix Solved Problems.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Orthogonal Matrix Solved Problems (a) suppose that a is an orthogonal matrix. Work the problems on your own and check your answers when you’re done. What kinds of matrices interact well with this notion of distance? But if the transpose of the matrix is equal to the inverse of the original matrix, then it is called an orthogonal matrix. If the transpose of a. Orthogonal Matrix Solved Problems.