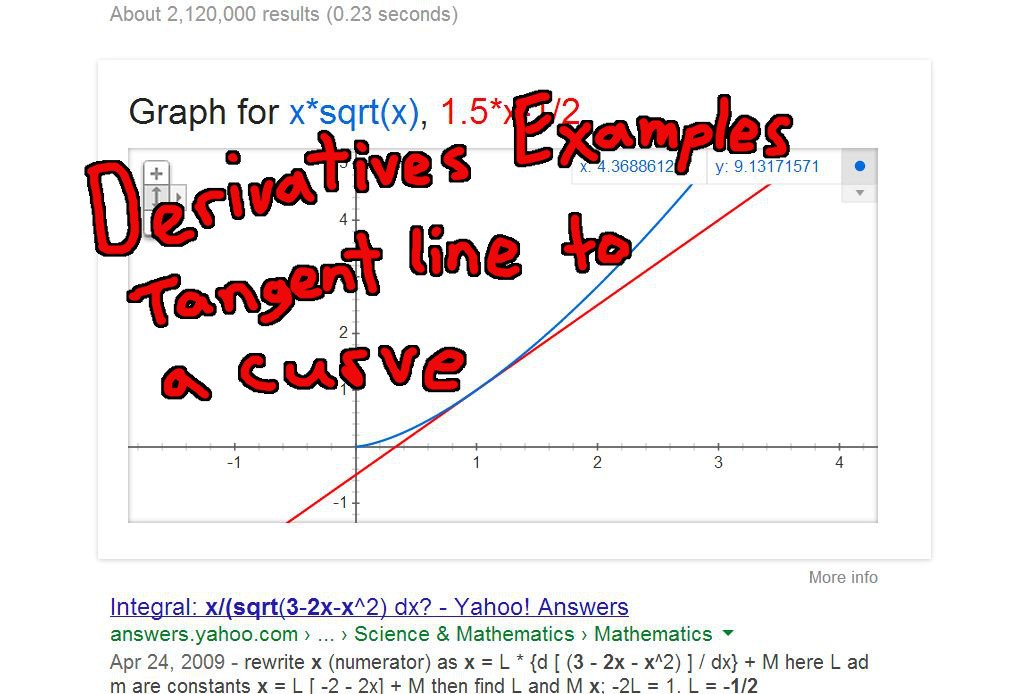
Tangent Line Vs Derivative at Charli Keyes blog

Tangent Line Vs Derivative. Is there a relationship between the trigonometric function tan(x) and the derivative of y with respect to x? The derivative of f(x) = x3 is f ′ (x) = 3x2, so f ′ (a) = f ′ (0) = 3(0)2. The derivative of a function \(f(x)\) at a value \(a\) is found using either of the definitions for the slope of the tangent line. The derivative of your function is the slope of the moving tangent line. The point (x,y) = (0,1) where the tangent intersects. Green marks positive derivative, red marks negative derivative and black marks zero derivative. This tool uses jqwidgets extensively. Then f(a) = f(0) = 03 = 0. Velocity is the rate of. Derivatives can help graph many functions. Its slope is the derivative; First, we know that the point p = (a,f (a)) p = (a, f (a)) will be on the tangent line. The first derivative of a function is the slope of the tangent line for any point on the function! Next, we’ll take a second point that is on the graph of the function, call it q= (x,f (x)) q = (x, f (x)) and. Use formula ( [eqn:tangentline]) with a = 0 and f(x) = x3.

Green marks positive derivative, red marks negative derivative and black marks zero derivative. Then f(a) = f(0) = 03 = 0. Therefore, it tells when the function is increasing,. The derivative of f(x) = x3 is f ′ (x) = 3x2, so f ′ (a) = f ′ (0) = 3(0)2. Is there a relationship between the trigonometric function tan(x) and the derivative of y with respect to x? The point (x,y) = (0,1) where the tangent intersects. Velocity is the rate of. The first derivative of a function is the slope of the tangent line for any point on the function! First, we know that the point p = (a,f (a)) p = (a, f (a)) will be on the tangent line. Derivatives can help graph many functions.

Derivatives Example Tangent Line to a Curve PeakD

Tangent Line Vs Derivative The derivative of your function is the slope of the moving tangent line. The first derivative of a function is the slope of the tangent line for any point on the function! Velocity is the rate of. Use formula ( [eqn:tangentline]) with a = 0 and f(x) = x3. Derivatives can help graph many functions. Green marks positive derivative, red marks negative derivative and black marks zero derivative. The derivative of your function is the slope of the moving tangent line. The derivative of f(x) = x3 is f ′ (x) = 3x2, so f ′ (a) = f ′ (0) = 3(0)2. Its slope is the derivative; Next, we’ll take a second point that is on the graph of the function, call it q= (x,f (x)) q = (x, f (x)) and. The derivative of a function \(f(x)\) at a value \(a\) is found using either of the definitions for the slope of the tangent line. The point (x,y) = (0,1) where the tangent intersects. First, we know that the point p = (a,f (a)) p = (a, f (a)) will be on the tangent line. Is there a relationship between the trigonometric function tan(x) and the derivative of y with respect to x? Therefore, it tells when the function is increasing,. Then f(a) = f(0) = 03 = 0.