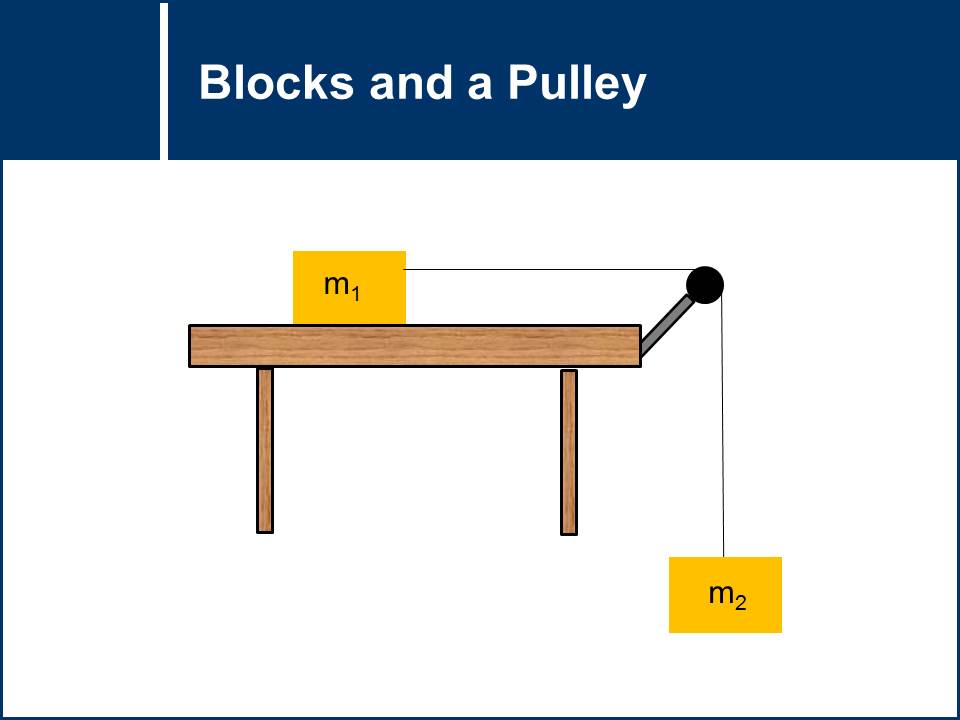
Acceleration Of Blocks On A Pulley . The goal of the problem is to calculate the accelerations of blocks 1 and 2. Like bms said, the ideal string. The solution of this problem is divided into four parts: Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. Given an incline with angle degrees which has a mass of kg placed upon it. Set up the system of equations. It is attached by a rope over a pulley to a mass of. Application of newton's second law to mass on incline with pulley. At point on the rim of the pulley has a tangential acceleration that is equal to the acceleration of the blocks so \[a=a_{\theta}=r \alpha_{z}. Two masses on a pulley. At time t = t 1, block 1 hits the ground. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. Let g denote the gravitational constant. At time t = 0, the blocks are released from rest.
from scienceres-edcp-educ.sites.olt.ubc.ca
Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. Like bms said, the ideal string. Application of newton's second law to mass on incline with pulley. At time t = t 1, block 1 hits the ground. Two masses on a pulley. You can assume that the rope is. Let g denote the gravitational constant. Given an incline with angle degrees which has a mass of kg placed upon it. The solution of this problem is divided into four parts:
Two Blocks and a Pulley MSTLTT
Acceleration Of Blocks On A Pulley Like bms said, the ideal string. Let g denote the gravitational constant. At time t = t 1, block 1 hits the ground. Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. Application of newton's second law to mass on incline with pulley. Like bms said, the ideal string. At time t = 0, the blocks are released from rest. It is attached by a rope over a pulley to a mass of. Given an incline with angle degrees which has a mass of kg placed upon it. The goal of the problem is to calculate the accelerations of blocks 1 and 2. Two masses on a pulley. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. You can assume that the rope is. At point on the rim of the pulley has a tangential acceleration that is equal to the acceleration of the blocks so \[a=a_{\theta}=r \alpha_{z}. The solution of this problem is divided into four parts: Set up the system of equations.
From www.youtube.com
Pulley with Friction 2 Blocks Newton's 2nd Law Dynamics YouTube Acceleration Of Blocks On A Pulley Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. The goal of the problem is to calculate the accelerations of blocks 1 and 2. You can assume that the rope is. Application of newton's second law to. Acceleration Of Blocks On A Pulley.
From www.youtube.com
Two Blocks Connected by String and a Pulley With Mass Find Acceleration Of Blocks On A Pulley Let g denote the gravitational constant. At point on the rim of the pulley has a tangential acceleration that is equal to the acceleration of the blocks so \[a=a_{\theta}=r \alpha_{z}. At time t = t 1, block 1 hits the ground. Two masses on a pulley. It is attached by a rope over a pulley to a mass of. Application. Acceleration Of Blocks On A Pulley.
From www.youtube.com
Pulley Physics Problem Finding Acceleration and Tension Force YouTube Acceleration Of Blocks On A Pulley The solution of this problem is divided into four parts: At time t = t 1, block 1 hits the ground. At point on the rim of the pulley has a tangential acceleration that is equal to the acceleration of the blocks so \[a=a_{\theta}=r \alpha_{z}. Two masses on a pulley. Like bms said, the ideal string. At time t =. Acceleration Of Blocks On A Pulley.
From www.doubtnut.com
Doubt Solutions Maths, Science, CBSE, NCERT, IIT JEE, NEET Acceleration Of Blocks On A Pulley The solution of this problem is divided into four parts: Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. The goal of the problem is to calculate the accelerations of blocks 1 and 2. Given an incline with angle degrees which has a mass of kg placed upon it. You can assume that the. Acceleration Of Blocks On A Pulley.
From byjus.com
how to find tensin and acceleration in a pulley moving upward with an Acceleration Of Blocks On A Pulley Like bms said, the ideal string. Let g denote the gravitational constant. It is attached by a rope over a pulley to a mass of. At time t = 0, the blocks are released from rest. Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. A 40 kg block on a level,. Acceleration Of Blocks On A Pulley.
From kunduz.com
[ANSWERED] 37 The acceleration of block B is Assuming pulley an Acceleration Of Blocks On A Pulley At time t = 0, the blocks are released from rest. Application of newton's second law to mass on incline with pulley. Let g denote the gravitational constant. Set up the system of equations. Given an incline with angle degrees which has a mass of kg placed upon it. Like bms said, the ideal string. The goal of the problem. Acceleration Of Blocks On A Pulley.
From www.toppr.com
Acceleration of pulleys and blocks are as shown in the figure. All Acceleration Of Blocks On A Pulley You can assume that the rope is. Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. Two masses on a pulley. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. Two masses of 80 kg and 140 kg hang. Acceleration Of Blocks On A Pulley.
From askfilo.com
15. The acceleration of block B is (Assuming pulley and strings are light.. Acceleration Of Blocks On A Pulley Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. At time t = 0, the blocks are released from rest. You can assume that the rope is. Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. At point on the rim of the pulley has a. Acceleration Of Blocks On A Pulley.
From byjus.com
Velocities of blocks A, B and pulley P 2 are shown in the figure given Acceleration Of Blocks On A Pulley Let g denote the gravitational constant. You can assume that the rope is. At time t = t 1, block 1 hits the ground. Given an incline with angle degrees which has a mass of kg placed upon it. Set up the system of equations. Application of newton's second law to mass on incline with pulley. Two masses of 80. Acceleration Of Blocks On A Pulley.
From www.toppr.com
Find the acceleration of two blocks. Assume pulleys and strings are Acceleration Of Blocks On A Pulley The goal of the problem is to calculate the accelerations of blocks 1 and 2. Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. You can assume that the rope is. It is attached by a rope over a pulley to a mass of. A 40 kg block on a level, frictionless table is. Acceleration Of Blocks On A Pulley.
From www.toppr.com
Consider the situation shown in figure. Both the pulleys and the string Acceleration Of Blocks On A Pulley At time t = t 1, block 1 hits the ground. Given an incline with angle degrees which has a mass of kg placed upon it. Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. It is attached by a rope over a pulley to a mass of. Two masses on a. Acceleration Of Blocks On A Pulley.
From www.youtube.com
Acceleration in the Atwood Machine when the Pulley has Mass, Moment of Acceleration Of Blocks On A Pulley Like bms said, the ideal string. At time t = t 1, block 1 hits the ground. Let g denote the gravitational constant. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. It is attached by a rope over a pulley to a mass of.. Acceleration Of Blocks On A Pulley.
From www.numerade.com
Two blocks are connected by a rope and pulley as shown below The mass Acceleration Of Blocks On A Pulley Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. At time t = t 1, block 1 hits the ground. Given an incline with angle degrees which has a mass of kg placed upon it. It is attached by a rope over a pulley to a mass of. At point on the rim of. Acceleration Of Blocks On A Pulley.
From www.youtube.com
Example Acceleration of block on a pulley YouTube Acceleration Of Blocks On A Pulley It is attached by a rope over a pulley to a mass of. Set up the system of equations. Given an incline with angle degrees which has a mass of kg placed upon it. The solution of this problem is divided into four parts: Two masses of 80 kg and 140 kg hang from a rope that runs over a. Acceleration Of Blocks On A Pulley.
From www.youtube.com
Acceleration of a Three Block Atwood Machine 3 Blocks 2 Pulleys, 2 Acceleration Of Blocks On A Pulley Let g denote the gravitational constant. Set up the system of equations. At point on the rim of the pulley has a tangential acceleration that is equal to the acceleration of the blocks so \[a=a_{\theta}=r \alpha_{z}. Application of newton's second law to mass on incline with pulley. Where δs represents the displacement, v0 represents the initial speed, and a represents. Acceleration Of Blocks On A Pulley.
From scienceres-edcp-educ.sites.olt.ubc.ca
Two Blocks and a Pulley MSTLTT Acceleration Of Blocks On A Pulley At time t = t 1, block 1 hits the ground. Let g denote the gravitational constant. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. At time t = 0, the blocks are released from rest. Given an incline with angle degrees which has. Acceleration Of Blocks On A Pulley.
From askfilo.com
Q.) Find acceleration of block \& Pulley 1. (given Pulley and Strings are.. Acceleration Of Blocks On A Pulley Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. The solution of this problem is divided into four parts: At time t = t 1, block 1 hits the ground. Given an incline with angle degrees which has a mass of kg placed upon it. Set up the system of equations. Like. Acceleration Of Blocks On A Pulley.
From criticalthinking.cloud
solving pulley system acceleration Acceleration Of Blocks On A Pulley Given an incline with angle degrees which has a mass of kg placed upon it. Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. It is attached by a rope over a pulley to a mass of. Application of newton's second law to mass on incline with pulley. The solution of this problem is. Acceleration Of Blocks On A Pulley.
From www.doubtnut.com
Doubt Solutions Maths, Science, CBSE, NCERT, IIT JEE, NEET Acceleration Of Blocks On A Pulley Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. The solution of this problem is divided into four parts: Application of newton's second law to mass on incline with pulley. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a. Acceleration Of Blocks On A Pulley.
From www.youtube.com
The magnitude of acceleration of blocks of mass 2 kg and 4 kg are a Acceleration Of Blocks On A Pulley At point on the rim of the pulley has a tangential acceleration that is equal to the acceleration of the blocks so \[a=a_{\theta}=r \alpha_{z}. Application of newton's second law to mass on incline with pulley. You can assume that the rope is. Set up the system of equations. The goal of the problem is to calculate the accelerations of blocks. Acceleration Of Blocks On A Pulley.
From www.slideserve.com
PPT Tension PowerPoint Presentation, free download ID6739131 Acceleration Of Blocks On A Pulley Given an incline with angle degrees which has a mass of kg placed upon it. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. At time t = t 1, block 1 hits the ground. You can assume that the rope is. It is attached. Acceleration Of Blocks On A Pulley.
From byjus.com
Figure shows an arrangement of blocks, pulleys, and strings. Strings Acceleration Of Blocks On A Pulley Set up the system of equations. Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. It is attached by a rope over a pulley to a mass of. Like bms said, the ideal string. At time t = t 1, block 1 hits the ground. Given an incline with angle degrees which. Acceleration Of Blocks On A Pulley.
From www.youtube.com
How to find the acceleration of blocks in basic pulley systems in Acceleration Of Blocks On A Pulley Like bms said, the ideal string. Given an incline with angle degrees which has a mass of kg placed upon it. Set up the system of equations. Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. At point on the rim of the pulley has a tangential acceleration that is equal to. Acceleration Of Blocks On A Pulley.
From www.toppr.com
A pulley with three blocks are shown in figure. Find acceleration and Acceleration Of Blocks On A Pulley Application of newton's second law to mass on incline with pulley. Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. You can assume that the rope is. The solution of this problem is divided into four parts: Let g denote the gravitational constant. It is attached by a rope over a pulley to a. Acceleration Of Blocks On A Pulley.
From www.doubtnut.com
Find the acceleration blocks in fig. The pulley and the string are Acceleration Of Blocks On A Pulley It is attached by a rope over a pulley to a mass of. Like bms said, the ideal string. Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. The solution of this problem is divided into four parts: At time t = 0, the blocks are released from rest. At time t. Acceleration Of Blocks On A Pulley.
From www.toppr.com
In the pulley system shown in the figure, if radii of the bigger and Acceleration Of Blocks On A Pulley The goal of the problem is to calculate the accelerations of blocks 1 and 2. Set up the system of equations. Two masses on a pulley. At time t = t 1, block 1 hits the ground. Like bms said, the ideal string. It is attached by a rope over a pulley to a mass of. You can assume that. Acceleration Of Blocks On A Pulley.
From www.toppr.com
A pulley with three blocks are shown in figure. Find acceleration and Acceleration Of Blocks On A Pulley At point on the rim of the pulley has a tangential acceleration that is equal to the acceleration of the blocks so \[a=a_{\theta}=r \alpha_{z}. Let g denote the gravitational constant. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. You can assume that the rope. Acceleration Of Blocks On A Pulley.
From www.pinterest.com
Acceleration with Friction Table with Pulley and Two Objects Physics Acceleration Of Blocks On A Pulley Where δs represents the displacement, v0 represents the initial speed, and a represents the acceleration. At time t = t 1, block 1 hits the ground. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. At time t = 0, the blocks are released from. Acceleration Of Blocks On A Pulley.
From www.doubtnut.com
In the pulleyblock arrangement shown in figure , find the relation Acceleration Of Blocks On A Pulley Application of newton's second law to mass on incline with pulley. Given an incline with angle degrees which has a mass of kg placed upon it. It is attached by a rope over a pulley to a mass of. You can assume that the rope is. At point on the rim of the pulley has a tangential acceleration that is. Acceleration Of Blocks On A Pulley.
From www.chegg.com
Solved Angular acceleration of a double pulley with two Acceleration Of Blocks On A Pulley At point on the rim of the pulley has a tangential acceleration that is equal to the acceleration of the blocks so \[a=a_{\theta}=r \alpha_{z}. Set up the system of equations. Application of newton's second law to mass on incline with pulley. The solution of this problem is divided into four parts: Where δs represents the displacement, v0 represents the initial. Acceleration Of Blocks On A Pulley.
From www.doubtnut.com
Doubt Solutions Maths, Science, CBSE, NCERT, IIT JEE, NEET Acceleration Of Blocks On A Pulley The goal of the problem is to calculate the accelerations of blocks 1 and 2. Set up the system of equations. At time t = t 1, block 1 hits the ground. At time t = 0, the blocks are released from rest. At point on the rim of the pulley has a tangential acceleration that is equal to the. Acceleration Of Blocks On A Pulley.
From www.doubtnut.com
The acceleration of the block A and B are Acceleration Of Blocks On A Pulley At time t = t 1, block 1 hits the ground. Application of newton's second law to mass on incline with pulley. The solution of this problem is divided into four parts: It is attached by a rope over a pulley to a mass of. Two masses on a pulley. A 40 kg block on a level, frictionless table is. Acceleration Of Blocks On A Pulley.
From www.doubtnut.com
In the pulleyblock arrangement shown in figure , find the relation be Acceleration Of Blocks On A Pulley Two masses on a pulley. At time t = 0, the blocks are released from rest. At time t = t 1, block 1 hits the ground. Given an incline with angle degrees which has a mass of kg placed upon it. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a. Acceleration Of Blocks On A Pulley.
From www.doubtnut.com
A pulleyropemass arrangement is shown in fig. Find the acceleration Acceleration Of Blocks On A Pulley You can assume that the rope is. Set up the system of equations. It is attached by a rope over a pulley to a mass of. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. Two masses of 80 kg and 140 kg hang from. Acceleration Of Blocks On A Pulley.
From www.youtube.com
Calculate Acceleration of Two Blocks Hanging From a Pulley Atwood's Acceleration Of Blocks On A Pulley Two masses of 80 kg and 140 kg hang from a rope that runs over a pulley. A 40 kg block on a level, frictionless table is connected to a 15 kg mass by a rope passing over a frictionless pulley. Two masses on a pulley. Where δs represents the displacement, v0 represents the initial speed, and a represents the. Acceleration Of Blocks On A Pulley.