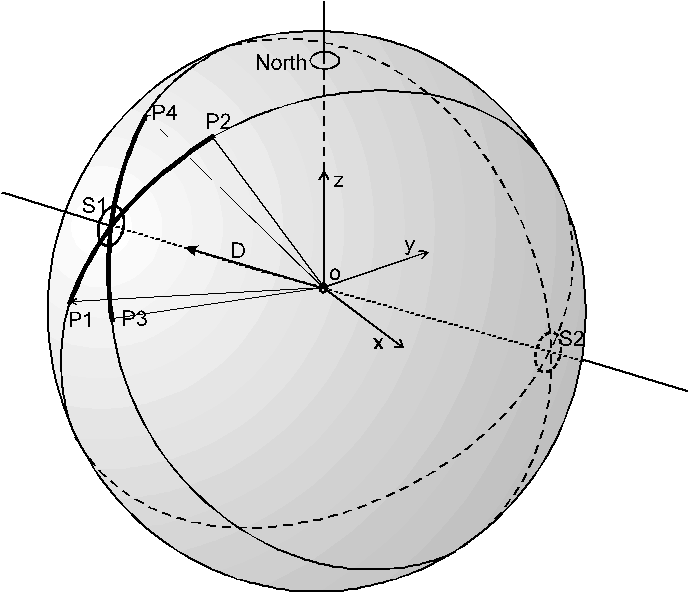
Spherical Mean Functions . Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. Spherical means of radial functions. By using spherical means and the above d'alembert. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. We investigate the boundedness properties of the.
from www.boeing-727.com
Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. We investigate the boundedness properties of the. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. By using spherical means and the above d'alembert. Spherical means of radial functions. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests.
Spherical Trigonometry
Spherical Mean Functions The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. By using spherical means and the above d'alembert. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. We investigate the boundedness properties of the. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. Spherical means of radial functions. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for.
From alakhag.github.io
Spherical Gaussians Alakh Aggarwal Spherical Mean Functions The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. Spherical means of radial functions. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. In essense,. Spherical Mean Functions.
From byjus.com
Area of Sphere Volume of Sphere Definitions & Examples Spherical Mean Functions In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. Spherical means of radial functions. The spherical. Spherical Mean Functions.
From www.researchgate.net
Examples of spherical functions. The grating orientation relative to Spherical Mean Functions Spherical means of radial functions. By using spherical means and the above d'alembert. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the. Spherical Mean Functions.
From en.citizendium.org
Spherical harmonics encyclopedia article Citizendium Spherical Mean Functions We investigate the boundedness properties of the. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. By using spherical means and the above d'alembert. Bessel functions for integer are also known as cylinder functions or the cylindrical. Spherical Mean Functions.
From mtex-toolbox.github.io
Harmonic Representation of Spherical Functions MTEX Spherical Mean Functions Spherical means of radial functions. We investigate the boundedness properties of the. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they. Spherical Mean Functions.
From tikz.net
Differential of Surface Area Spherical Coordinates Spherical Mean Functions Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. We investigate the boundedness properties of the. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. In essense, the spherical mean m h (x, r). Spherical Mean Functions.
From tikz.net
Differential Volume in Spherical Coordinates Spherical Mean Functions We investigate the boundedness properties of the. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests.. Spherical Mean Functions.
From www.studypool.com
SOLUTION The Secret of THE RANGE OF THE SPHERICAL MEAN VALUE OPERATOR Spherical Mean Functions Spherical means of radial functions. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. We investigate. Spherical Mean Functions.
From mathsathome.com
How to Calculate the Volume of a Spherical Cap Spherical Mean Functions Spherical means of radial functions. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. The spherical. Spherical Mean Functions.
From www.researchgate.net
Types of spherical harmonics. Left sectoral spherical harmonic (a Spherical Mean Functions The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. Bessel functions for integer are also. Spherical Mean Functions.
From mathinsight.org
Spherical coordinates Math Insight Spherical Mean Functions The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. By using spherical means and the above d'alembert. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already. Spherical Mean Functions.
From www.researchgate.net
4 Visualization of spherical cost function defined by (Eq. 7.13) using Spherical Mean Functions In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. Spherical means of radial functions. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. The. Spherical Mean Functions.
From mathworld.wolfram.com
Spherical Harmonic from Wolfram MathWorld Spherical Mean Functions We investigate the boundedness properties of the. Spherical means of radial functions. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r. Spherical Mean Functions.
From calconcalculator.com
Spherical Coordinates Calculator with steps Definition Spherical Mean Functions Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. Spherical means of radial functions. We investigate the boundedness properties of the. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. In essense, the spherical mean m h (x, r) is just the average of h over. Spherical Mean Functions.
From kr.mathworks.com
Spherical Coordinates MATLAB & Simulink MathWorks 한국 Spherical Mean Functions Spherical means of radial functions. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. We investigate the boundedness properties of the. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. By using spherical means and the. Spherical Mean Functions.
From www.researchgate.net
The spherical coordinate system, where θ ∈ [0, π ] is the polar angle Spherical Mean Functions Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. Spherical means of radial functions. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. We investigate the boundedness properties of the. By using spherical means and. Spherical Mean Functions.
From www.youtube.com
Spherical Geometry Deriving The Formula For The Area Of A Spherical Spherical Mean Functions By using spherical means and the above d'alembert. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution. Spherical Mean Functions.
From www.slideserve.com
PPT For an animation of spherical coordinates visit PowerPoint Spherical Mean Functions The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. We investigate the boundedness properties of the. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$.. Spherical Mean Functions.
From mathinsight.org
Spherical coordinates Math Insight Spherical Mean Functions The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. By using spherical means and the above d'alembert. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. The spherical mean value operator plays an equal prominent role. Spherical Mean Functions.
From www.slideserve.com
PPT Spherical Extent Functions PowerPoint Presentation, free download Spherical Mean Functions By using spherical means and the above d'alembert. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. We investigate the boundedness properties of the. The spherical mean value operator plays an equal prominent role for recent imaging techniques. Spherical Mean Functions.
From www.slideserve.com
PPT Chapter 24 PowerPoint Presentation, free download ID520042 Spherical Mean Functions Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. By using spherical means and the above. Spherical Mean Functions.
From www.semanticscholar.org
[PDF] Inversion of Spherical Means and the Wave Equation in Even Spherical Mean Functions The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. Spherical means of radial functions. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. By using. Spherical Mean Functions.
From www.studocu.com
Educ216 Spherical Trigonometry Concepts and Example Studocu Spherical Mean Functions Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is. Spherical Mean Functions.
From commons.wikimedia.org
FileSpherical mean.png Wikimedia Commons Spherical Mean Functions Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. In essense, the spherical mean m h. Spherical Mean Functions.
From www.boeing-727.com
Spherical Trigonometry Spherical Mean Functions In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. We investigate the boundedness properties of the. By using spherical means and the above d'alembert. Spherical means of. Spherical Mean Functions.
From www.researchgate.net
(PDF) Diagonal spherical means Spherical Mean Functions The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered at x, as the name suggests. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in. Spherical Mean Functions.
From www.slideserve.com
PPT Spherical Extent Functions PowerPoint Presentation, free download Spherical Mean Functions The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. By using spherical means and the above d'alembert. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. We investigate the boundedness properties of the. Spherical means. Spherical Mean Functions.
From mathinsight.org
Spherical coordinates Math Insight Spherical Mean Functions The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. By using spherical means and the above d'alembert. We investigate the boundedness properties of the. Spherical means. Spherical Mean Functions.
From www.researchgate.net
Local Groupcentric spherical mean densities as a function of Spherical Mean Functions The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. Spherical means of radial functions. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of. Spherical Mean Functions.
From www.researchgate.net
Illustration of the real valued spherical harmonic basis functions Spherical Mean Functions Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. We investigate the boundedness properties of the.. Spherical Mean Functions.
From www.youtube.com
How to get the gradient of 1/r in spherical coordinates YouTube Spherical Mean Functions The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. Spherical means of radial functions. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. We investigate the boundedness properties of the. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they. Spherical Mean Functions.
From mathinsight.org
Spherical coordinates Math Insight Spherical Mean Functions The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. By using spherical means and the above d'alembert. We investigate the boundedness properties of the. The spherical mean value operator plays an equal prominent role for recent imaging techniques. Spherical Mean Functions.
From www.studypool.com
SOLUTION The Secret of THE RANGE OF THE SPHERICAL MEAN VALUE OPERATOR Spherical Mean Functions Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. Spherical means of radial functions. By using spherical means and the above d'alembert. In essense, the spherical mean m h (x, r) is just the average of h over the surface of a sphere of radius r centered. Spherical Mean Functions.
From www.studypool.com
SOLUTION The Secret of THE RANGE OF THE SPHERICAL MEAN VALUE OPERATOR Spherical Mean Functions The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to. Spherical means of radial functions. By using spherical means and the above d'alembert. The spherical mean of. Spherical Mean Functions.
From www.physicsbootcamp.org
Electric Field for Spherical Symmetry Spherical Mean Functions We investigate the boundedness properties of the. The spherical mean of $h(x,y,z)=x=x_0+x'=x_0+r \sin\theta\cos\phi$ is given by $i_1+i_2$. By using spherical means and the above d'alembert. Spherical means of radial functions. The spherical mean value operator plays an equal prominent role for recent imaging techniques as the classical radon transform does already for. In essense, the spherical mean m h . Spherical Mean Functions.