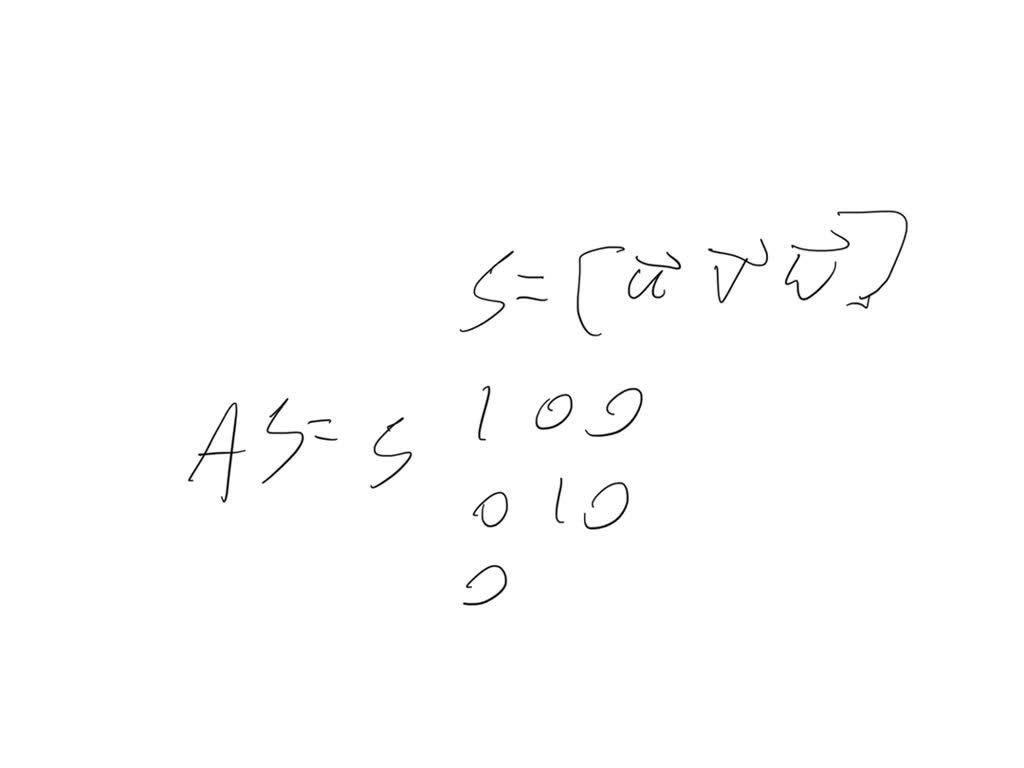Matrix Of Orthogonal Projection Onto A Plane . According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. Its shadow) qy = ˆy in the. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). Chose a basis b∞ of the kernel of. You see already that the image of a t is.
from www.numerade.com
Its shadow) qy = ˆy in the. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. You see already that the image of a t is. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Chose a basis b∞ of the kernel of. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a.
SOLVEDIf matrix A represents the orthogonal projection onto a plane V
Matrix Of Orthogonal Projection Onto A Plane You see already that the image of a t is. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. Its shadow) qy = ˆy in the. You see already that the image of a t is. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). Chose a basis b∞ of the kernel of.
From ar.inspiredpencil.com
Orthogonal Projection Matrix Matrix Of Orthogonal Projection Onto A Plane We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. You see already that the image of a t is. Learn the basic properties of orthogonal projections as linear transformations and as. Matrix Of Orthogonal Projection Onto A Plane.
From www.researchgate.net
Illustration of (a) two orthogonal projection vectors w x and w y (1 × Matrix Of Orthogonal Projection Onto A Plane Chose a basis b∞ of the kernel of. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. You see already that the image of a t is. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. There are many. Matrix Of Orthogonal Projection Onto A Plane.
From ar.inspiredpencil.com
Orthogonal Projection Matrix Matrix Of Orthogonal Projection Onto A Plane According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro. Matrix Of Orthogonal Projection Onto A Plane.
From www.youtube.com
Finding standard matrix of orthogonal projection onto a plane YouTube Matrix Of Orthogonal Projection Onto A Plane Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Its shadow) qy = ˆy in the. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Chose a basis b∞. Matrix Of Orthogonal Projection Onto A Plane.
From www.coursehero.com
[Solved] Orthogonal Projection onto Plane Find an expression for Matrix Of Orthogonal Projection Onto A Plane Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. Chose a basis b∞ of. Matrix Of Orthogonal Projection Onto A Plane.
From www.numerade.com
SOLVED Determine the matrix of the orthogonal projection on the plane Matrix Of Orthogonal Projection Onto A Plane There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. Chose a basis b∞ of the kernel. Matrix Of Orthogonal Projection Onto A Plane.
From www.chegg.com
6. Find the standard matrix for the orthogonal Matrix Of Orthogonal Projection Onto A Plane According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. We will call later the. Matrix Of Orthogonal Projection Onto A Plane.
From www.cs.princeton.edu
Parallel Projection Matrix Matrix Of Orthogonal Projection Onto A Plane A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Its shadow) qy = ˆy in. Matrix Of Orthogonal Projection Onto A Plane.
From ar.inspiredpencil.com
Orthogonal Projection Matrix Matrix Of Orthogonal Projection Onto A Plane According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. We will call later the. Matrix Of Orthogonal Projection Onto A Plane.
From www.numerade.com
SOLVED HW11.6. Projection matrix of the orthogonal complement to a Matrix Of Orthogonal Projection Onto A Plane Its shadow) qy = ˆy in the. According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. Chose a basis b∞ of the kernel of. There are many ways to show that. Matrix Of Orthogonal Projection Onto A Plane.
From www.researchgate.net
Representation of the orthogonal projection of M Y (t) onto the plane Matrix Of Orthogonal Projection Onto A Plane According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. You see already that the image of a t is. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the. Matrix Of Orthogonal Projection Onto A Plane.
From www.slideserve.com
PPT Projection PowerPoint Presentation, free download ID7009345 Matrix Of Orthogonal Projection Onto A Plane For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. We will call later the matrix. Matrix Of Orthogonal Projection Onto A Plane.
From www.vrogue.co
Standard Matrix Of A Orthogonal Projection Linear Tra vrogue.co Matrix Of Orthogonal Projection Onto A Plane Chose a basis b∞ of the kernel of. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. Its shadow) qy = ˆy in the. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we. Matrix Of Orthogonal Projection Onto A Plane.
From www.vrogue.co
Standard Matrix Of A Orthogonal Projection Linear Tra vrogue.co Matrix Of Orthogonal Projection Onto A Plane You see already that the image of a t is. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t =. Matrix Of Orthogonal Projection Onto A Plane.
From www.chegg.com
Solved Q3.1 Matrix of Orthogonal Projection 35 Points Find Matrix Of Orthogonal Projection Onto A Plane You see already that the image of a t is. Chose a basis b∞ of the kernel of. According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). Learn the basic. Matrix Of Orthogonal Projection Onto A Plane.
From ar.inspiredpencil.com
Orthogonal Projection Matrix Matrix Of Orthogonal Projection Onto A Plane There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Its shadow) qy = ˆy in the. Chose a basis b∞ of the kernel of. Learn the basic properties of orthogonal projections as linear transformations. Matrix Of Orthogonal Projection Onto A Plane.
From www.youtube.com
Orthogonal projection of a vector onto a plane. YouTube Matrix Of Orthogonal Projection Onto A Plane Its shadow) qy = ˆy in the. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). For an orthogonal projection p there is a basis in which the matrix is diagonal and. Matrix Of Orthogonal Projection Onto A Plane.
From heung-bae-lee.github.io
Least Squares Problem & Orthogonal Projection DataLatte's IT Blog Matrix Of Orthogonal Projection Onto A Plane Chose a basis b∞ of the kernel of. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. You see already that the image of a t is. According to our derivation above, the projection. Matrix Of Orthogonal Projection Onto A Plane.
From www.vrogue.co
Standard Matrix Of A Orthogonal Projection Linear Tra vrogue.co Matrix Of Orthogonal Projection Onto A Plane Its shadow) qy = ˆy in the. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). Chose a basis b∞ of the kernel of. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. Learn the basic properties of. Matrix Of Orthogonal Projection Onto A Plane.
From www.chegg.com
Solved Problem 7. (Orthogonal Projections onto a plane of Matrix Of Orthogonal Projection Onto A Plane There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Chose a basis b∞ of the kernel of. We will call later the matrix at, obtained by switching rows and columns of athe transpose of. Matrix Of Orthogonal Projection Onto A Plane.
From www.youtube.com
Orthogonal projection matrix onto the nullspace YouTube Matrix Of Orthogonal Projection Onto A Plane Chose a basis b∞ of the kernel of. You see already that the image of a t is. According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. Learn. Matrix Of Orthogonal Projection Onto A Plane.
From www.numerade.com
SOLVEDIf matrix A represents the orthogonal projection onto a plane V Matrix Of Orthogonal Projection Onto A Plane We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Its shadow) qy = ˆy in the. For an. Matrix Of Orthogonal Projection Onto A Plane.
From www.vrogue.co
Standard Matrix Of A Orthogonal Projection Linear Tra vrogue.co Matrix Of Orthogonal Projection Onto A Plane Its shadow) qy = ˆy in the. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. For an orthogonal projection. Matrix Of Orthogonal Projection Onto A Plane.
From www.youtube.com
Projection onto plane YouTube Matrix Of Orthogonal Projection Onto A Plane A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. You see already that the image of a t is. According to our derivation above, the projection matrix q maps a vector y. Matrix Of Orthogonal Projection Onto A Plane.
From www.slideserve.com
PPT The Projection Matrix PowerPoint Presentation, free download ID Matrix Of Orthogonal Projection Onto A Plane According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. You see already that the image of a t is. For an orthogonal projection p there is a basis in which the matrix is diagonal and. Matrix Of Orthogonal Projection Onto A Plane.
From www.vrogue.co
Standard Matrix Of A Orthogonal Projection Linear Tra vrogue.co Matrix Of Orthogonal Projection Onto A Plane For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. Its shadow) qy = ˆy in the. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). According to our derivation above, the projection matrix q maps a vector y. Matrix Of Orthogonal Projection Onto A Plane.
From www.studyxapp.com
find the projection matrix of the orthogonal projection onto the Matrix Of Orthogonal Projection Onto A Plane We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. Its shadow) qy = ˆy in the. According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. There are many ways to show that e = b − p = b axˆ. Matrix Of Orthogonal Projection Onto A Plane.
From heung-bae-lee.github.io
Least Squares Problem & Orthogonal Projection DataLatte's IT Blog Matrix Of Orthogonal Projection Onto A Plane Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. Chose a basis b∞ of the kernel of. There are many ways to show that e = b − p = b axˆ is orthogonal to. Matrix Of Orthogonal Projection Onto A Plane.
From www.chegg.com
Solved C. Find the standard matrix C of the orthogonal Matrix Of Orthogonal Projection Onto A Plane Its shadow) qy = ˆy in the. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix) if \(p^2 = p\) and \(p^t = p\). For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. There are many ways to show that e = b − p =. Matrix Of Orthogonal Projection Onto A Plane.
From www.geogebra.org
Orthogonal Projection Onto xyPlane GeoGebra Matrix Of Orthogonal Projection Onto A Plane According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. Chose. Matrix Of Orthogonal Projection Onto A Plane.
From www.chegg.com
Solved HW11.2. Projection matrix of a projection onto a line Matrix Of Orthogonal Projection Onto A Plane You see already that the image of a t is. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only 0 and 1. A matrix \(p\) is an orthogonal projector (or orthogonal projection matrix). Matrix Of Orthogonal Projection Onto A Plane.
From www.cs.princeton.edu
Perspective Projection Matrix Matrix Of Orthogonal Projection Onto A Plane According to our derivation above, the projection matrix q maps a vector y 2 rn to its orthogonal projection (i.e. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Chose a basis b∞ of. Matrix Of Orthogonal Projection Onto A Plane.
From www.youtube.com
Cross Product Matrix and Orthogonal Projection onto a Plane YouTube Matrix Of Orthogonal Projection Onto A Plane There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Its shadow) qy = ˆy in the. For an orthogonal projection p there is a basis in which the matrix is diagonal and contains only. Matrix Of Orthogonal Projection Onto A Plane.
From rilohs.weebly.com
Orthogonal matrix rilohs Matrix Of Orthogonal Projection Onto A Plane Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. There are many ways to show that e = b − p = b axˆ is orthogonal to the plane we’re pro jecting onto, after which we can use the fact that − e is. Chose a basis b∞ of the kernel of. For an orthogonal. Matrix Of Orthogonal Projection Onto A Plane.
From www.youtube.com
Linear Transformations Projection of X and Y Axis Using 2x2 Matrix Matrix Of Orthogonal Projection Onto A Plane Its shadow) qy = ˆy in the. We will call later the matrix at, obtained by switching rows and columns of athe transpose of a. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Chose a basis b∞ of the kernel of. You see already that the image of a t is. There are many. Matrix Of Orthogonal Projection Onto A Plane.