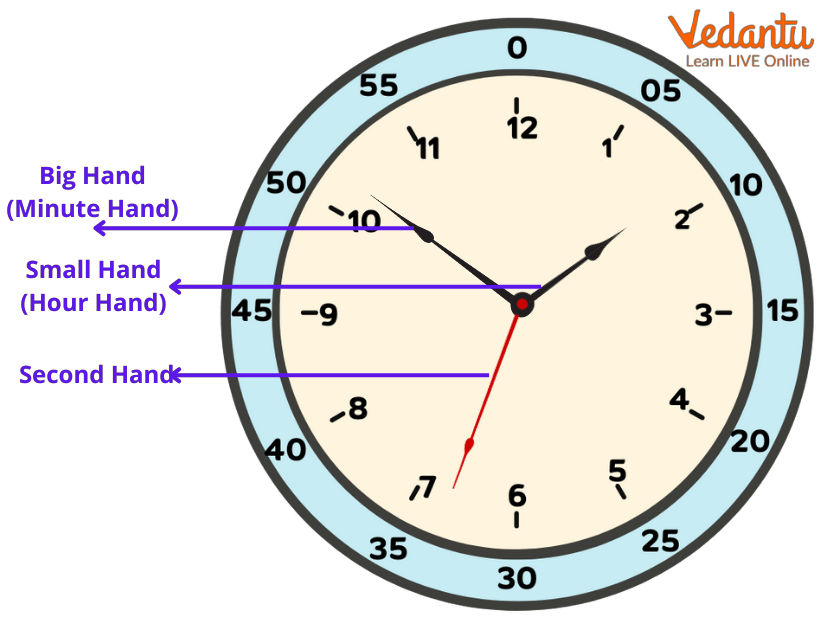
How Many Times Do A Clock's Hands Overlap In One Day . When and how many times a day do a clock’s hands overlap? Thus, a clock's hands cross each other 22 times per day. That means, if you divide 12/11, you should get the length of each. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. We, therefore, obtain t = t/12 + n for n overlaps. In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. The first overlap occurs after t = 12/11 hours or around 1:05 am. The minute hand would have completed two more circuits than the hour hand the second time they overlapped. Asked 6 years, 6 months ago.
from www.vedantu.com
At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. Asked 6 years, 6 months ago. We, therefore, obtain t = t/12 + n for n overlaps. The first overlap occurs after t = 12/11 hours or around 1:05 am. When and how many times a day do a clock’s hands overlap? In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. That means, if you divide 12/11, you should get the length of each. Thus, a clock's hands cross each other 22 times per day. The minute hand would have completed two more circuits than the hour hand the second time they overlapped.
Hour Hand on Clock Learn Definition, Facts and Examples
How Many Times Do A Clock's Hands Overlap In One Day We, therefore, obtain t = t/12 + n for n overlaps. Thus, a clock's hands cross each other 22 times per day. The minute hand would have completed two more circuits than the hour hand the second time they overlapped. We, therefore, obtain t = t/12 + n for n overlaps. The first overlap occurs after t = 12/11 hours or around 1:05 am. Asked 6 years, 6 months ago. When and how many times a day do a clock’s hands overlap? In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. That means, if you divide 12/11, you should get the length of each. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock.
From www.resourcequeue.com
How Many Times Do a Clock’s Hands Overlap in A Day? How Many Times Do A Clock's Hands Overlap In One Day At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when. How Many Times Do A Clock's Hands Overlap In One Day.
From www.numberphile.com
When do clock hands overlap? — Numberphile How Many Times Do A Clock's Hands Overlap In One Day The minute hand would have completed two more circuits than the hour hand the second time they overlapped. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can. How Many Times Do A Clock's Hands Overlap In One Day.
From interestingengineering.com
Have You Ever Wondered How Many Times a Clock's Hands Overlap in a Day? How Many Times Do A Clock's Hands Overlap In One Day From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. That means, if you divide 12/11, you should get the length of each. Thus, a clock's hands cross each other 22 times per day. The minute hand would have completed two more circuits than the hour. How Many Times Do A Clock's Hands Overlap In One Day.
From www.youtube.com
How Many Times are the Clock's Hands at Right Angles During a 24 Hour How Many Times Do A Clock's Hands Overlap In One Day In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. Thus, a clock's hands cross each other 22 times per day. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. Asked 6 years,. How Many Times Do A Clock's Hands Overlap In One Day.
From infinitesimallysmall.com
When Do A Clock’s Hands Overlap? The Other Side Of Mathematics How Many Times Do A Clock's Hands Overlap In One Day That means, if you divide 12/11, you should get the length of each. We, therefore, obtain t = t/12 + n for n overlaps. In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. When and how many times a day do a clock’s hands overlap? At first,. How Many Times Do A Clock's Hands Overlap In One Day.
From karakais.blogspot.com
Kais's blog How many times do a clock's hands overlap in a day How Many Times Do A Clock's Hands Overlap In One Day That means, if you divide 12/11, you should get the length of each. Thus, a clock's hands cross each other 22 times per day. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. Asked 6 years, 6 months ago. When and how many times a. How Many Times Do A Clock's Hands Overlap In One Day.
From www.youtube.com
TRICKY IAS INTERVIEW QUESTIONSHow many times in a day does a clocks How Many Times Do A Clock's Hands Overlap In One Day The minute hand would have completed two more circuits than the hour hand the second time they overlapped. We, therefore, obtain t = t/12 + n for n overlaps. Asked 6 years, 6 months ago. In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. That means, if. How Many Times Do A Clock's Hands Overlap In One Day.
From cerpflwq.blob.core.windows.net
How Many Times During The Day Do The Hands Of A Clock Overlap at Mary How Many Times Do A Clock's Hands Overlap In One Day We, therefore, obtain t = t/12 + n for n overlaps. That means, if you divide 12/11, you should get the length of each. When and how many times a day do a clock’s hands overlap? In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. The minute. How Many Times Do A Clock's Hands Overlap In One Day.
From fyobkyyye.blob.core.windows.net
How Many Times Per Day Does A Clock's Hands Overlap at Roy Thatcher blog How Many Times Do A Clock's Hands Overlap In One Day When and how many times a day do a clock’s hands overlap? In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. We, therefore, obtain t = t/12 + n for n overlaps. At first, it might be tempting to just say “24,” but the correct answer is. How Many Times Do A Clock's Hands Overlap In One Day.
From exosnwhyu.blob.core.windows.net
How Many Times Do A Clock S Hands Overlap Each Day at Jill Baker blog How Many Times Do A Clock's Hands Overlap In One Day The first overlap occurs after t = 12/11 hours or around 1:05 am. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock. How Many Times Do A Clock's Hands Overlap In One Day.
From www.livecareer.com
Times Clock Hands Overlap? Interview Questions LiveCareer How Many Times Do A Clock's Hands Overlap In One Day At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. The minute hand would have completed two more circuits than the hour hand the second time they overlapped.. How Many Times Do A Clock's Hands Overlap In One Day.
From www.youtube.com
How Many Times do hands of clock coincide in a dayMaths trick for How Many Times Do A Clock's Hands Overlap In One Day We, therefore, obtain t = t/12 + n for n overlaps. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. Thus, a clock's hands cross each other 22 times per day. The minute hand would have completed two more circuits than the hour hand the. How Many Times Do A Clock's Hands Overlap In One Day.
From www.youtube.com
How many times do the clock hands overlap in 24 hours? YouTube How Many Times Do A Clock's Hands Overlap In One Day At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. Thus, a clock's hands cross each other 22 times per day. The minute hand would have completed two. How Many Times Do A Clock's Hands Overlap In One Day.
From www.bbc.co.uk
Hours and days Maths Learning with BBC Bitesize BBC Bitesize How Many Times Do A Clock's Hands Overlap In One Day That means, if you divide 12/11, you should get the length of each. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. We, therefore, obtain t = t/12 + n for n overlaps. Thus, a clock's hands cross each other 22 times per day. Asked. How Many Times Do A Clock's Hands Overlap In One Day.
From www.youtube.com
To Figure Out Exactly When Clock's Hands OverlapHow Do Clock's Hands How Many Times Do A Clock's Hands Overlap In One Day The first overlap occurs after t = 12/11 hours or around 1:05 am. That means, if you divide 12/11, you should get the length of each. We, therefore, obtain t = t/12 + n for n overlaps. From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1. How Many Times Do A Clock's Hands Overlap In One Day.
From www.vedantu.com
Hour Hand on Clock Learn Definition, Facts and Examples How Many Times Do A Clock's Hands Overlap In One Day From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. Asked 6 years, 6 months ago. We, therefore, obtain t = t/12 + n for n overlaps. That means, if you divide 12/11, you should get the length of each. At first, it might be tempting. How Many Times Do A Clock's Hands Overlap In One Day.
From www.youtube.com
4 ways of solving the Overlapping Clock Hands Problem YouTube How Many Times Do A Clock's Hands Overlap In One Day That means, if you divide 12/11, you should get the length of each. In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. Asked 6 years, 6 months ago. When and how many times a day do a clock’s hands overlap? From 12 midnight we know the hands. How Many Times Do A Clock's Hands Overlap In One Day.
From www.animalia-life.club
Analog Clock Hands How Many Times Do A Clock's Hands Overlap In One Day Thus, a clock's hands cross each other 22 times per day. The minute hand would have completed two more circuits than the hour hand the second time they overlapped. The first overlap occurs after t = 12/11 hours or around 1:05 am. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can. How Many Times Do A Clock's Hands Overlap In One Day.
From www.youtube.com
HOW MANY TIMES IN A DAY,ARE THE HANDS OF A CLOCK IN STRAIGHT LINE BUT How Many Times Do A Clock's Hands Overlap In One Day From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. That means, if you divide 12/11, you should get the length of each. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock. How Many Times Do A Clock's Hands Overlap In One Day.
From hr.mathigon.org
Overlapping Hands of a Clock Mathigon How Many Times Do A Clock's Hands Overlap In One Day From 12 midnight we know the hands will not overlap for at least 60 minutes of time when the time will be 1 o’clock. That means, if you divide 12/11, you should get the length of each. The first overlap occurs after t = 12/11 hours or around 1:05 am. In order to get back to being lined up at. How Many Times Do A Clock's Hands Overlap In One Day.
From exosnwhyu.blob.core.windows.net
How Many Times Do A Clock S Hands Overlap Each Day at Jill Baker blog How Many Times Do A Clock's Hands Overlap In One Day The minute hand would have completed two more circuits than the hour hand the second time they overlapped. In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised. How Many Times Do A Clock's Hands Overlap In One Day.
From fyobkyyye.blob.core.windows.net
How Many Times Per Day Does A Clock's Hands Overlap at Roy Thatcher blog How Many Times Do A Clock's Hands Overlap In One Day At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. The first overlap occurs after t = 12/11 hours or around 1:05 am. Asked 6 years, 6 months. How Many Times Do A Clock's Hands Overlap In One Day.
From exosnwhyu.blob.core.windows.net
How Many Times Do A Clock S Hands Overlap Each Day at Jill Baker blog How Many Times Do A Clock's Hands Overlap In One Day At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. Asked 6 years, 6 months ago. The minute hand would have completed two more circuits than the hour. How Many Times Do A Clock's Hands Overlap In One Day.
From finwise.edu.vn
Top 94+ Pictures How Many Times Do Clock Hands Overlap Updated How Many Times Do A Clock's Hands Overlap In One Day Asked 6 years, 6 months ago. In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20,. How Many Times Do A Clock's Hands Overlap In One Day.
From www.splashlearn.com
What is Time? Definition, Uses, Conversion, Measurement, Example How Many Times Do A Clock's Hands Overlap In One Day Thus, a clock's hands cross each other 22 times per day. Asked 6 years, 6 months ago. We, therefore, obtain t = t/12 + n for n overlaps. That means, if you divide 12/11, you should get the length of each. In order to get back to being lined up at noon, the hands must pass each other 11 times. How Many Times Do A Clock's Hands Overlap In One Day.
From exosnwhyu.blob.core.windows.net
How Many Times Do A Clock S Hands Overlap Each Day at Jill Baker blog How Many Times Do A Clock's Hands Overlap In One Day In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. Asked 6 years, 6 months ago. The minute hand would have completed two more circuits than the hour hand the second time they overlapped. Thus, a clock's hands cross each other 22 times per day. When and how. How Many Times Do A Clock's Hands Overlap In One Day.
From www.studypool.com
SOLUTION Overlap Clock Hands Studypool How Many Times Do A Clock's Hands Overlap In One Day That means, if you divide 12/11, you should get the length of each. Thus, a clock's hands cross each other 22 times per day. The minute hand would have completed two more circuits than the hour hand the second time they overlapped. We, therefore, obtain t = t/12 + n for n overlaps. When and how many times a day. How Many Times Do A Clock's Hands Overlap In One Day.
From www.youtube.com
How Many Times do a Clock's Hands Make a 45 Degree Angle During a 24 How Many Times Do A Clock's Hands Overlap In One Day Asked 6 years, 6 months ago. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. Thus, a clock's hands cross each other 22 times per day. That. How Many Times Do A Clock's Hands Overlap In One Day.
From fyobkyyye.blob.core.windows.net
How Many Times Per Day Does A Clock's Hands Overlap at Roy Thatcher blog How Many Times Do A Clock's Hands Overlap In One Day At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a day. In order to get back to being lined up at noon, the hands must pass each other 11. How Many Times Do A Clock's Hands Overlap In One Day.
From quizandriddles.com
How many times do the hands of a clock overlap in a day? Daily Quiz How Many Times Do A Clock's Hands Overlap In One Day In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. Asked 6 years, 6 months ago. The first overlap occurs after t = 12/11 hours or around 1:05 am. That means, if you divide 12/11, you should get the length of each. At first, it might be tempting. How Many Times Do A Clock's Hands Overlap In One Day.
From cerpflwq.blob.core.windows.net
How Many Times During The Day Do The Hands Of A Clock Overlap at Mary How Many Times Do A Clock's Hands Overlap In One Day That means, if you divide 12/11, you should get the length of each. In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. The minute hand would have completed two more circuits than the hour hand the second time they overlapped. When and how many times a day. How Many Times Do A Clock's Hands Overlap In One Day.
From exosnwhyu.blob.core.windows.net
How Many Times Do A Clock S Hands Overlap Each Day at Jill Baker blog How Many Times Do A Clock's Hands Overlap In One Day We, therefore, obtain t = t/12 + n for n overlaps. When and how many times a day do a clock’s hands overlap? The first overlap occurs after t = 12/11 hours or around 1:05 am. In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. Asked 6. How Many Times Do A Clock's Hands Overlap In One Day.
From fyobkyyye.blob.core.windows.net
How Many Times Per Day Does A Clock's Hands Overlap at Roy Thatcher blog How Many Times Do A Clock's Hands Overlap In One Day The first overlap occurs after t = 12/11 hours or around 1:05 am. Asked 6 years, 6 months ago. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can be surmised because the clock hands approximately overlap at 12:00, 1:05, 2:10, 3:15, 4:20, 5:25, 6:30, 7:35, 8:40, 9:45 and 10:50 twice a. How Many Times Do A Clock's Hands Overlap In One Day.
From www.youtube.com
Interview puzzles with answersHow many times do all hands of clock How Many Times Do A Clock's Hands Overlap In One Day When and how many times a day do a clock’s hands overlap? We, therefore, obtain t = t/12 + n for n overlaps. Asked 6 years, 6 months ago. That means, if you divide 12/11, you should get the length of each. At first, it might be tempting to just say “24,” but the correct answer is “22.” this can. How Many Times Do A Clock's Hands Overlap In One Day.
From finwise.edu.vn
Top 94+ Pictures How Many Times Do Clock Hands Overlap Updated How Many Times Do A Clock's Hands Overlap In One Day In order to get back to being lined up at noon, the hands must pass each other 11 times every 12 hours. That means, if you divide 12/11, you should get the length of each. The first overlap occurs after t = 12/11 hours or around 1:05 am. From 12 midnight we know the hands will not overlap for at. How Many Times Do A Clock's Hands Overlap In One Day.