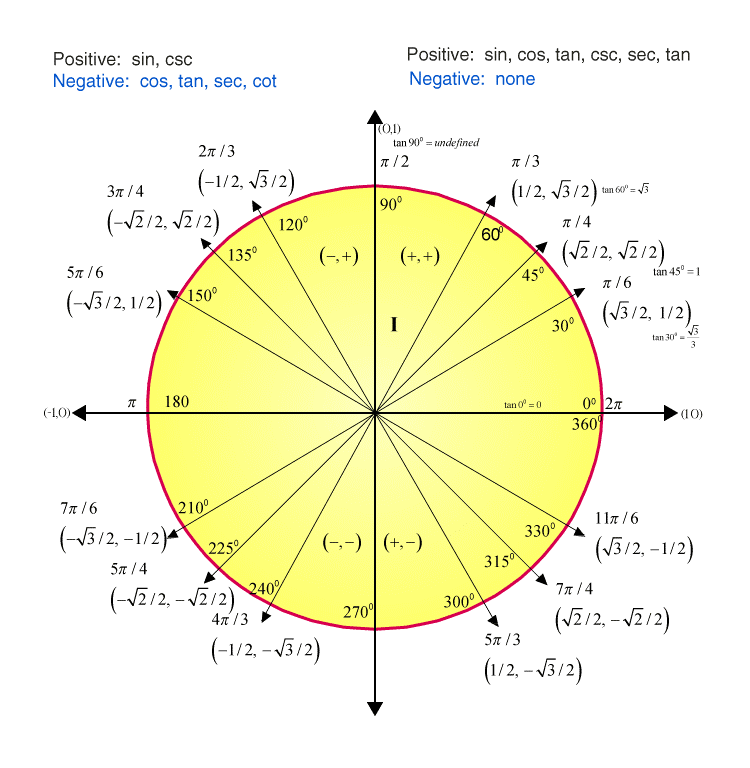
Unit Circle Triangles . The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Defining sine, cosine, and tangent ratios for any angle. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. Understand unit circle, reference angle, terminal side, standard position. Find the exact trigonometric function values for angles.
from
Defining sine, cosine, and tangent ratios for any angle. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Find the exact trigonometric function values for angles. To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). Understand unit circle, reference angle, terminal side, standard position.
Unit Circle Triangles Understand unit circle, reference angle, terminal side, standard position. Find the exact trigonometric function values for angles. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Understand unit circle, reference angle, terminal side, standard position. Defining sine, cosine, and tangent ratios for any angle. To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way.
From templatelab.com
42 Printable Unit Circle Charts & Diagrams (Sin, Cos, Tan, Cot etc) Unit Circle Triangles The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Defining sine, cosine, and tangent ratios for any angle. Find the exact trigonometric function values for angles. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. Understand unit circle, reference angle, terminal. Unit Circle Triangles.
From
Unit Circle Triangles Understand unit circle, reference angle, terminal side, standard position. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Defining sine, cosine, and tangent ratios for any angle. Find the exact trigonometric function values for angles. The unit circle is. Unit Circle Triangles.
From www.ck12.org
Trigonometric Ratios on the Unit Circle CK12 Foundation Unit Circle Triangles The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). Find the exact trigonometric function values for angles. Defining sine,. Unit Circle Triangles.
From
Unit Circle Triangles Find the exact trigonometric function values for angles. Defining sine, cosine, and tangent ratios for any angle. Understand unit circle, reference angle, terminal side, standard position. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \. Unit Circle Triangles.
From tuningpp.com
unit circle trig values chart Unit Circle Triangles Understand unit circle, reference angle, terminal side, standard position. To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Defining sine, cosine, and tangent ratios for any angle. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). To define our trigonometric. Unit Circle Triangles.
From izgdipkcgw.blogspot.com
How To Use The Unit Circle Meaning, something exciting to remember Unit Circle Triangles To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. The angle (in radians) that \(t\) intercepts forms an arc. Unit Circle Triangles.
From etc.usf.edu
Unit Circle Labeled In 45° Increments With Values ClipArt ETC Unit Circle Triangles To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). The angle (in radians) that \(t\) intercepts forms an. Unit Circle Triangles.
From mathbooks.unl.edu
MFG The Unit Circle Unit Circle Triangles Defining sine, cosine, and tangent ratios for any angle. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Understand unit circle, reference angle, terminal side, standard position. The. Unit Circle Triangles.
From
Unit Circle Triangles Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). Find the exact trigonometric. Unit Circle Triangles.
From
Unit Circle Triangles Understand unit circle, reference angle, terminal side, standard position. Find the exact trigonometric function values for angles. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). To define our trigonometric. Unit Circle Triangles.
From
Unit Circle Triangles The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Find the exact trigonometric function values for angles. Defining sine, cosine, and tangent ratios for any angle. To define our trigonometric functions,. Unit Circle Triangles.
From www.mometrix.com
Unit Circles and Standard Position (Video & Practice Questions) Unit Circle Triangles To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Find the exact trigonometric. Unit Circle Triangles.
From trigunitcircle.weebly.com
Triangles in a Unit Circle Trigonometry Unit Circle Unit Circle Triangles To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). The unit circle is a circle with a radius. Unit Circle Triangles.
From
Unit Circle Triangles Understand unit circle, reference angle, terminal side, standard position. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). To define our trigonometric functions, we begin by drawing a unit circle, a circle. Unit Circle Triangles.
From
Unit Circle Triangles Find the exact trigonometric function values for angles. Understand unit circle, reference angle, terminal side, standard position. To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). The unit circle is a circle with a radius of 1 that shows the angles and sides of. Unit Circle Triangles.
From www.onlinemathlearning.com
Special Triangles & Unit Circle (examples, solutions, videos, lessons Unit Circle Triangles Understand unit circle, reference angle, terminal side, standard position. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. To define our trigonometric functions, we begin by drawing a unit circle, a circle. Unit Circle Triangles.
From
Unit Circle Triangles Find the exact trigonometric function values for angles. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. Understand unit circle, reference angle, terminal side, standard position. To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with. Unit Circle Triangles.
From
Unit Circle Triangles Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). Defining sine, cosine, and tangent ratios for any angle. The angle (in radians) that \(t\) intercepts forms. Unit Circle Triangles.
From
Unit Circle Triangles Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. Understand unit circle, reference angle, terminal side, standard position. To define our trigonometric ratios, we begin by drawing a. Unit Circle Triangles.
From
Unit Circle Triangles To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Defining sine, cosine, and tangent ratios for any angle. To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\).. Unit Circle Triangles.
From
Unit Circle Triangles Understand unit circle, reference angle, terminal side, standard position. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Defining sine, cosine, and tangent ratios for any angle. To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Find the exact trigonometric. Unit Circle Triangles.
From
Unit Circle Triangles The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Defining sine, cosine, and tangent ratios for any angle. To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). Find the exact trigonometric function values for angles. Understand unit circle, reference. Unit Circle Triangles.
From www.animalia-life.club
Blank Unit Circle Quadrant I Unit Circle Triangles The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Understand unit circle, reference angle, terminal side, standard position. Defining sine,. Unit Circle Triangles.
From www.slideserve.com
PPT Trigonometric Ratios in the Unit Circle PowerPoint Presentation Unit Circle Triangles To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Defining sine, cosine, and tangent ratios for any angle. Understand unit circle, reference angle, terminal side, standard position. Find the exact trigonometric function values for angles. The unit circle is a circle with a radius. Unit Circle Triangles.
From www.mometrix.com
Unit Circles and Standard Position (Video & Practice Questions) Unit Circle Triangles The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. Understand unit circle, reference angle, terminal side, standard position. Learn how to use the unit circle to define trigonometric functions such as sine,. Unit Circle Triangles.
From
Unit Circle Triangles Understand unit circle, reference angle, terminal side, standard position. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Find the exact trigonometric function values for angles. To define our trigonometric ratios, we begin by drawing a unit circle (a. Unit Circle Triangles.
From brilliant.org
Unit Circle Brilliant Math & Science Wiki Unit Circle Triangles To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). Understand unit circle, reference angle, terminal side, standard position. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Learn how to use the unit circle to define trigonometric functions such. Unit Circle Triangles.
From www.slideserve.com
PPT THE UNIT CIRCLE PowerPoint Presentation, free download ID6015505 Unit Circle Triangles To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Understand unit circle, reference angle, terminal side, standard position. To define our trigonometric functions, we begin by drawing a unit circle, a. Unit Circle Triangles.
From
Unit Circle Triangles The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). The angle (in radians) that \(t\) intercepts forms an arc of. Unit Circle Triangles.
From www.cuemath.com
Unit circle Solved Examples Geometry Cuemath Unit Circle Triangles To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Find the exact trigonometric function values for angles. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Defining sine, cosine, and tangent ratios for any angle. The. Unit Circle Triangles.
From calcworkshop.com
Unit Circle w/ Everything (Charts, Worksheets, 35+ Examples) Unit Circle Triangles Understand unit circle, reference angle, terminal side, standard position. To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure \(\pageindex{2}\). Find the exact trigonometric function values for angles. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Defining sine, cosine, and. Unit Circle Triangles.
From science.howstuffworks.com
How to Use the Unit Circle in Trigonometry HowStuffWorks Unit Circle Triangles The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \. Unit Circle Triangles.
From
Unit Circle Triangles To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Understand unit circle, reference angle, terminal side, standard position. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. Learn how. Unit Circle Triangles.
From
Unit Circle Triangles Find the exact trigonometric function values for angles. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \ (1\) centered at the origin \ ( (0,0)\)). Defining sine, cosine,. Unit Circle Triangles.
From squarerootofnegativeoneteachmath.blogspot.com
square root of negative one teach math Unit Circle Philosophy Unit Circle Triangles Defining sine, cosine, and tangent ratios for any angle. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Understand unit circle, reference angle, terminal side, standard position. The unit circle is a circle with a radius of 1 that shows the angles and sides of right triangles in a standard way. To. Unit Circle Triangles.