Linear Operator Is Continuous At A Point . given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. Let us assume it is continuous. the range of a linear operator is a subspace of y. A linear operator on a normed space x (to a normed space y) is continuous at every point. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. i'm trying to prove that if a linear operator is continuous, then it is bounded. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. a linear continuous operator m :
from machinelearningmastery.com
i'm trying to prove that if a linear operator is continuous, then it is bounded. A linear operator on a normed space x (to a normed space y) is continuous at every point. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. a linear continuous operator m : if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. Let us assume it is continuous. the range of a linear operator is a subspace of y. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow.
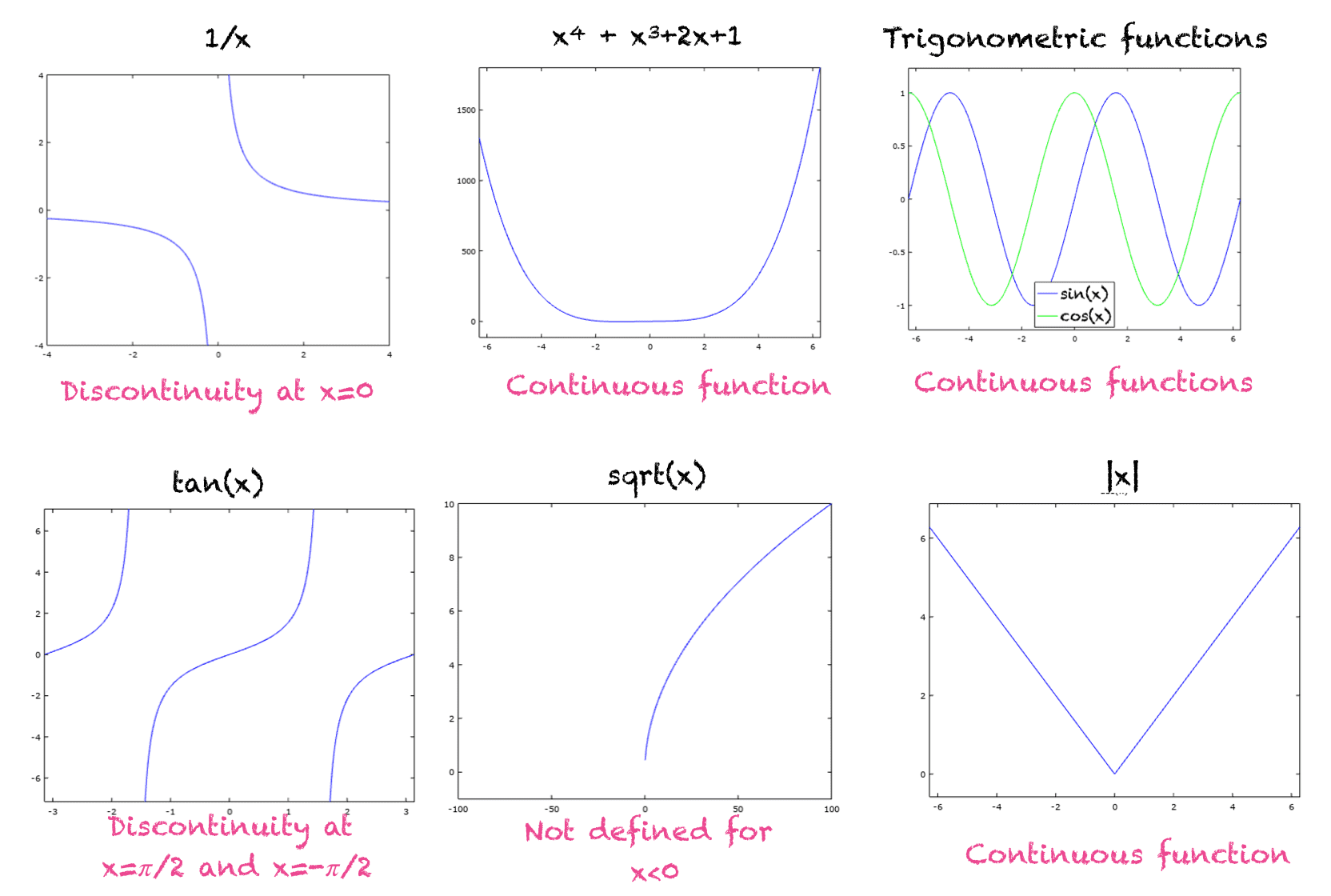
A Gentle Introduction to Continuous Functions
Linear Operator Is Continuous At A Point Let us assume it is continuous. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. A linear operator on a normed space x (to a normed space y) is continuous at every point. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. i'm trying to prove that if a linear operator is continuous, then it is bounded. Let us assume it is continuous. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. a linear continuous operator m : the range of a linear operator is a subspace of y.
From www.studocu.com
Examples of linear operatorfunctional Msc. Maths Studocu Linear Operator Is Continuous At A Point the range of a linear operator is a subspace of y. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. Let us assume it is continuous. i'm trying to prove that if a linear operator is. Linear Operator Is Continuous At A Point.
From www.chegg.com
Solved Question 4 (1 point) A linear operator is linear Linear Operator Is Continuous At A Point if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. A linear operator on a normed space x (to a normed space y) is continuous at every point. i'm trying to prove that if a linear operator is continuous, then it is bounded. . Linear Operator Is Continuous At A Point.
From www.youtube.com
Examples of Linear Operators Linear Algebra YouTube Linear Operator Is Continuous At A Point a linear continuous operator m : the range of a linear operator is a subspace of y. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. i'm trying to prove that if a linear operator is continuous, then it is bounded. Let us assume it is continuous. if t is continuous at a. Linear Operator Is Continuous At A Point.
From www.youtube.com
6 MTH641Functional Analysis Topic 64+65 A linear operator is Linear Operator Is Continuous At A Point an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. i'm trying to prove that if a linear operator is continuous, then it is bounded. Let us assume it is continuous. a linear continuous operator m : the range of a linear operator is a subspace of y.. Linear Operator Is Continuous At A Point.
From math.stackexchange.com
functional analysis derivative of a linear operator Mathematics Linear Operator Is Continuous At A Point A linear operator on a normed space x (to a normed space y) is continuous at every point. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. an operator that is linear and continuous on a linear submanifold of a topological vector space. Linear Operator Is Continuous At A Point.
From www.researchgate.net
(PDF) New Types of Continuous Linear Operator in Probabilistic Normed Space Linear Operator Is Continuous At A Point A linear operator on a normed space x (to a normed space y) is continuous at every point. i'm trying to prove that if a linear operator is continuous, then it is bounded. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. a linear continuous operator m : an operator that is linear and. Linear Operator Is Continuous At A Point.
From www.youtube.com
Composition of Linear Operators YouTube Linear Operator Is Continuous At A Point C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. Let us assume it is continuous. A linear operator on a normed space x (to a normed space y) is. Linear Operator Is Continuous At A Point.
From www.slideserve.com
PPT Lecture 21 Continuous Problems Fr é chet Derivatives PowerPoint Linear Operator Is Continuous At A Point Let us assume it is continuous. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. the range of a linear operator is. Linear Operator Is Continuous At A Point.
From www.youtube.com
Calculus Continuous Functions how to determine continuity of a Linear Operator Is Continuous At A Point Let us assume it is continuous. i'm trying to prove that if a linear operator is continuous, then it is bounded. a linear continuous operator m : C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset. Linear Operator Is Continuous At A Point.
From www.studocu.com
Lecture notes 21 Lecture 21 Linear Operators and Geometry 1 Linear Linear Operator Is Continuous At A Point an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. the range of a linear operator is a subspace of y. a linear continuous operator m : Let us assume it is continuous. A linear operator on a normed space x (to a normed space y) is continuous at. Linear Operator Is Continuous At A Point.
From lms.su.edu.pk
SU LMS Linear Operator Is Continuous At A Point Let us assume it is continuous. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. A linear operator on a normed space x (to a normed space y) is continuous at every point. the range of a linear operator is a subspace of. Linear Operator Is Continuous At A Point.
From exomdjudt.blob.core.windows.net
Continuous Linear Functional Definition at Vilma Vinson blog Linear Operator Is Continuous At A Point the range of a linear operator is a subspace of y. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. Let us assume it is continuous. a linear continuous operator m : given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. if t is. Linear Operator Is Continuous At A Point.
From www.youtube.com
Matrix Representation of a Linear Operator (method II) YouTube Linear Operator Is Continuous At A Point an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. Let us assume it is continuous. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset. Linear Operator Is Continuous At A Point.
From www.chegg.com
Solved Let L be the linear operator in R2 defined by Linear Operator Is Continuous At A Point i'm trying to prove that if a linear operator is continuous, then it is bounded. A linear operator on a normed space x (to a normed space y) is continuous at every point. Let us assume it is continuous. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. an operator that is linear and continuous. Linear Operator Is Continuous At A Point.
From www.slideserve.com
PPT Lecture 20 Continuous Problems Linear Operators and Their Linear Operator Is Continuous At A Point a linear continuous operator m : if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. A linear operator on a normed space x (to a normed space y) is continuous at every point. C (δ) → c (δ) is a multiplier of the. Linear Operator Is Continuous At A Point.
From jtdaugherty.github.io
Continuous Functions Derivative Works Linear Operator Is Continuous At A Point C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. Let us assume it is continuous. A linear operator on a normed space x (to a normed space y) is continuous at every point. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. an operator. Linear Operator Is Continuous At A Point.
From www.youtube.com
9 Semigroups of linear operators Strongly continuous semigroups and Linear Operator Is Continuous At A Point the range of a linear operator is a subspace of y. A linear operator on a normed space x (to a normed space y) is continuous at every point. i'm trying to prove that if a linear operator is continuous, then it is bounded. a linear continuous operator m : an operator that is linear and. Linear Operator Is Continuous At A Point.
From www.numerade.com
SOLVEDProve that a) A linear combination of completely continuous Linear Operator Is Continuous At A Point a linear continuous operator m : C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. A linear operator on a normed space x (to a normed space y) is continuous at every point. an operator that is linear and continuous on a linear submanifold of a. Linear Operator Is Continuous At A Point.
From www.youtube.com
Matrix representation of an operator YouTube Linear Operator Is Continuous At A Point given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. Let us assume it is continuous. a linear continuous operator m : i'm trying to prove that if a linear operator is continuous, then it is bounded. C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ. Linear Operator Is Continuous At A Point.
From www.youtube.com
Linear Algebra 24, Dot Product as a Linear Operator 1 YouTube Linear Operator Is Continuous At A Point C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. an. Linear Operator Is Continuous At A Point.
From machinelearningmastery.com
A Gentle Introduction to Continuous Functions Linear Operator Is Continuous At A Point A linear operator on a normed space x (to a normed space y) is continuous at every point. a linear continuous operator m : given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. Let us. Linear Operator Is Continuous At A Point.
From www.slideserve.com
PPT Solving Schrodinger Equation PowerPoint Presentation, free Linear Operator Is Continuous At A Point the range of a linear operator is a subspace of y. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. Let us assume it is continuous. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is. Linear Operator Is Continuous At A Point.
From slidetodoc.com
Chapter 2 Mathematical Tools of Quantum Mechanics Hilbert Linear Operator Is Continuous At A Point given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. a linear continuous operator m : Let us assume it is continuous. i'm trying to prove that if a linear operator. Linear Operator Is Continuous At A Point.
From www.youtube.com
Matrix representation of a Linear Operator YouTube Linear Operator Is Continuous At A Point the range of a linear operator is a subspace of y. C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. a linear continuous operator m : . Linear Operator Is Continuous At A Point.
From www.slideserve.com
PPT Functional Analysis PowerPoint Presentation, free download ID Linear Operator Is Continuous At A Point an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. A linear operator on a normed space x (to a normed space y) is continuous at. Linear Operator Is Continuous At A Point.
From www.chegg.com
Solved Let P,QR + R be continuous, and define the linear Linear Operator Is Continuous At A Point an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. i'm trying to prove that if a linear operator is continuous, then it is bounded.. Linear Operator Is Continuous At A Point.
From www.studypool.com
SOLUTION Bounded and continuous linear operators Studypool Linear Operator Is Continuous At A Point C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. A linear operator on a normed space x (to a normed space y) is continuous at every point. given. Linear Operator Is Continuous At A Point.
From www.slideserve.com
PPT IllPosedness and Regularization of Linear Operators (1 lecture Linear Operator Is Continuous At A Point Let us assume it is continuous. a linear continuous operator m : i'm trying to prove that if a linear operator is continuous, then it is bounded. A linear operator on a normed space x (to a normed space y) is continuous at every point. an operator that is linear and continuous on a linear submanifold of. Linear Operator Is Continuous At A Point.
From www.slideserve.com
PPT CONTINUITY & DIFFERENTIABILITY PowerPoint Presentation, free Linear Operator Is Continuous At A Point given a linear operator on normed vector spaces $t:\mathcal{d}(t)\subset x \rightarrow. a linear continuous operator m : C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. A. Linear Operator Is Continuous At A Point.
From www.chegg.com
Solved Problem 9. Consider the linear operator LR2 + R2 Linear Operator Is Continuous At A Point C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. the range of a linear operator is a subspace of y. i'm. Linear Operator Is Continuous At A Point.
From www.yumpu.com
Lecture 8 5 Linear Operators Linear Operator Is Continuous At A Point if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. i'm trying to prove that if a linear operator is continuous, then it is bounded. A linear operator on a normed space x (to a normed space y) is continuous at every point. Let. Linear Operator Is Continuous At A Point.
From www.youtube.com
Continuous or Bounded Linear Operators Functional Analysis Lecture Linear Operator Is Continuous At A Point the range of a linear operator is a subspace of y. an operator that is linear and continuous on a linear submanifold of a topological vector space is automatically. if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. A linear operator on. Linear Operator Is Continuous At A Point.
From www.chegg.com
Solved 2. Determine if the given function is continuous or Linear Operator Is Continuous At A Point if t is continuous at a single point $x_0$ implies t is continuous at $0$ then, it proves that if t is continuous at. Let us assume it is continuous. C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. the range of a linear operator is. Linear Operator Is Continuous At A Point.
From www.youtube.com
LO 52 Determine if a vector valued function is continuous at a point Linear Operator Is Continuous At A Point a linear continuous operator m : i'm trying to prove that if a linear operator is continuous, then it is bounded. the range of a linear operator is a subspace of y. A linear operator on a normed space x (to a normed space y) is continuous at every point. Let us assume it is continuous. . Linear Operator Is Continuous At A Point.
From www.slideserve.com
PPT Molecular Mechanics & Quantum Chemistry PowerPoint Presentation Linear Operator Is Continuous At A Point A linear operator on a normed space x (to a normed space y) is continuous at every point. C (δ) → c (δ) is a multiplier of the dimovski convolution * φ given by (4) with φ of the. the range of a linear operator is a subspace of y. Let us assume it is continuous. given a. Linear Operator Is Continuous At A Point.