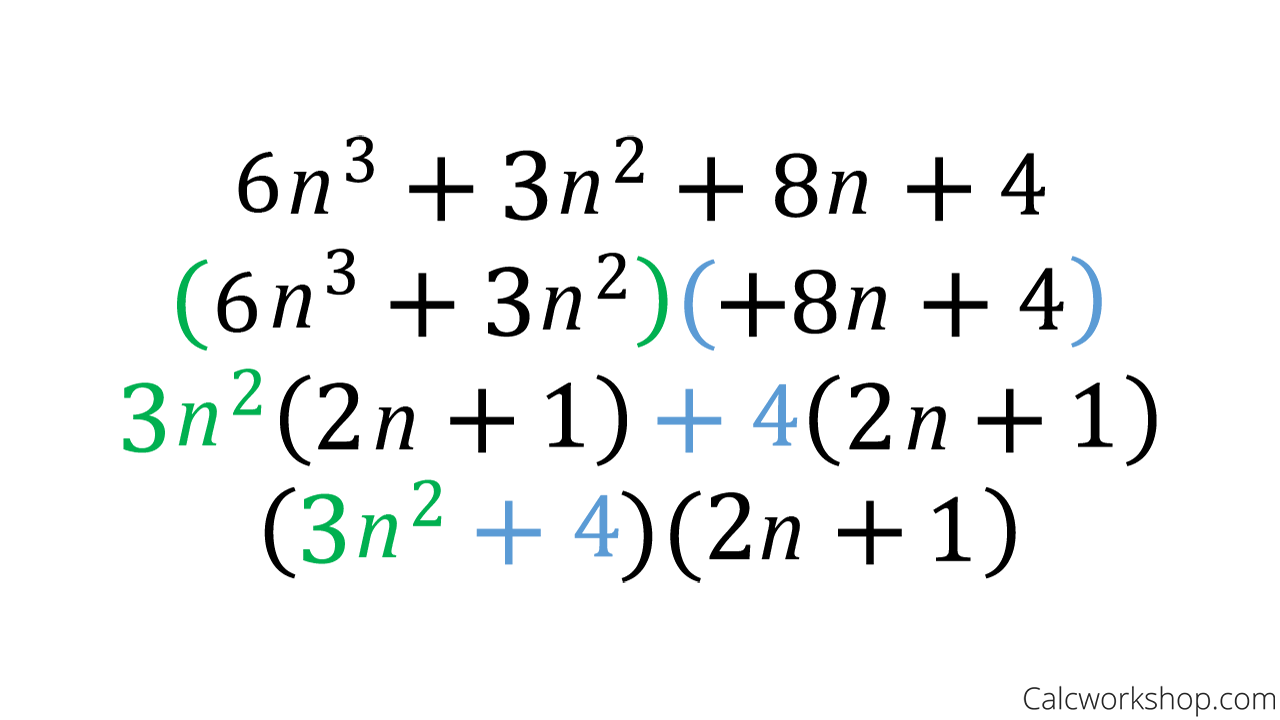Group Ring Examples . A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. Rotations of objects, symmetries in physics. Is associative, i.e., (a · b) · c =. Ring (r,+,·) is a set and · , such that: What are some examples of groups, rings, and fields in real life? M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. R, together with two binary operations, denoted by +. (r,+) is an abelian group. Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law.
from calcworkshop.com
What are some examples of groups, rings, and fields in real life? Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. (r,+) is an abelian group. Ring (r,+,·) is a set and · , such that: Rotations of objects, symmetries in physics. Is associative, i.e., (a · b) · c =. A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. R, together with two binary operations, denoted by +. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for.
How to Factor by Grouping? (15+ Amazing Examples!)
Group Ring Examples Rotations of objects, symmetries in physics. Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. Rotations of objects, symmetries in physics. What are some examples of groups, rings, and fields in real life? R, together with two binary operations, denoted by +. Is associative, i.e., (a · b) · c =. Ring (r,+,·) is a set and · , such that: M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; (r,+) is an abelian group.
From www.slideserve.com
PPT PART I Symmetric Ciphers CHAPTER 4 Finite Fields 4.1 Groups Group Ring Examples Ring (r,+,·) is a set and · , such that: R, together with two binary operations, denoted by +. Is associative, i.e., (a · b) · c =. Rotations of objects, symmetries in physics. What are some examples of groups, rings, and fields in real life? Informal definitions a group is a set in which you can perform one operation. Group Ring Examples.
From www.slideserve.com
PPT Network Coding AAU Summer School Finite Fields PowerPoint Group Ring Examples A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; Rotations of objects, symmetries in physics. Ring (r,+,·) is a set and · , such that: Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us). Group Ring Examples.
From www.researchgate.net
Illustration of several grouping principles. Adapted from " Perceptual Group Ring Examples Ring (r,+,·) is a set and · , such that: Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. R, together with two binary operations, denoted by +. Examples of axioms of type (∀) for r are commutativity and associativity of both + and. Group Ring Examples.
From mathsux.org
Factor By Grouping Examples Algebra Math Lessons Group Ring Examples What are some examples of groups, rings, and fields in real life? R, together with two binary operations, denoted by +. Ring (r,+,·) is a set and · , such that: Is associative, i.e., (a · b) · c =. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Informal definitions a group is a set in. Group Ring Examples.
From hillhouse4design.com
factoring by grouping examples Group Ring Examples Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. Ring (r,+,·) is a set and · , such that: (r,+) is an abelian group. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. R, together with two binary operations, denoted by. Group Ring Examples.
From www.teachthought.com
How To Use Flexible Grouping In The Classroom Group Ring Examples Ring (r,+,·) is a set and · , such that: What are some examples of groups, rings, and fields in real life? Rotations of objects, symmetries in physics. R, together with two binary operations, denoted by +. Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. (r,+) is. Group Ring Examples.
From teachingandlearningmedia.weebly.com
Grouping Notes TEACHING & LEARNING MEDIA Group Ring Examples Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. R, together with two binary operations, denoted by +. What are some examples of groups, rings, and fields in real life? M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Ring (r,+,·) is a set and. Group Ring Examples.
From www.youtube.com
Groups&RingsLinear AlgebraIntroductionGroupRingFieldB.A.B Group Ring Examples M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. Is associative, i.e., (a · b) · c =. Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication. Group Ring Examples.
From www.youtube.com
Algebraic Structures Groups, Rings, and Fields YouTube Group Ring Examples Ring (r,+,·) is a set and · , such that: A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; Is associative, i.e., (a · b) · c =. R, together with two binary operations, denoted by +. M1 → m2 of abelian groups such that α(rm1) =. Group Ring Examples.
From www.teachthought.com
How To Use Flexible Grouping In The Classroom Group Ring Examples Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Is associative, i.e., (a · b) · c =. A ring (with identity) is a set r together with two binary operations + and (called addition and. Group Ring Examples.
From edpd593finalproject.weebly.com
Flexible Groupings Differentiated Instruction Group Ring Examples Ring (r,+,·) is a set and · , such that: What are some examples of groups, rings, and fields in real life? (r,+) is an abelian group. Is associative, i.e., (a · b) · c =. Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. A ring (with. Group Ring Examples.
From www.slideserve.com
PPT PART I Symmetric Ciphers CHAPTER 4 Finite Fields 4.1 Groups Group Ring Examples What are some examples of groups, rings, and fields in real life? Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; M1 → m2 of abelian. Group Ring Examples.
From www.slideserve.com
PPT Cryptography and Network Security PowerPoint Presentation, free Group Ring Examples R, together with two binary operations, denoted by +. (r,+) is an abelian group. Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. Ring (r,+,·) is a set and · , such that: Examples of axioms of type (∀) for r are commutativity and. Group Ring Examples.
From kmr.csc.kth.se
Group, Ring, Field, Module, Vector Space Knowledge Management Group Ring Examples A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. R, together with two binary operations, denoted by +. (r,+) is an abelian group. Ring (r,+,·) is a set and · , such that: What are. Group Ring Examples.
From atpamsplaceblog.blogspot.com
Grouping Students in the Classroom Pam's PlaceTeach.Inspire.Learn Group Ring Examples What are some examples of groups, rings, and fields in real life? Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; M1. Group Ring Examples.
From worksheetlistch.z13.web.core.windows.net
Factoring By Grouping Examples With Answers Group Ring Examples R, together with two binary operations, denoted by +. Rotations of objects, symmetries in physics. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. What are some examples of groups, rings, and. Group Ring Examples.
From www.youtube.com
12. Ring Ring with unity Commutative ring Examples of ring Group Ring Examples What are some examples of groups, rings, and fields in real life? R, together with two binary operations, denoted by +. (r,+) is an abelian group. Is associative, i.e., (a · b) · c =. A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; M1 → m2. Group Ring Examples.
From www.slideserve.com
PPT Cryptography and Network Security Chapter 4 PowerPoint Group Ring Examples (r,+) is an abelian group. Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. What are some examples of groups, rings, and fields in real life? A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a;. Group Ring Examples.
From www.picozu.com
Mastering Image Grouping in A Comprehensive Guide Picozu Group Ring Examples A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Is associative, i.e., (a · b) · c =. Informal definitions a group is a set in which you can perform one operation (usually addition or. Group Ring Examples.
From www.youtube.com
AES I Group, Ring, Field and Finite Field Abstract Algebra Basics Group Ring Examples M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Rotations of objects, symmetries in physics. Ring (r,+,·) is a set and · , such that: Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. (r,+) is an abelian group. What are. Group Ring Examples.
From awesomeenglish.edu.vn
Discover more than 146 algebra ring theory super hot awesomeenglish Group Ring Examples Ring (r,+,·) is a set and · , such that: A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. What are some examples of groups, rings, and fields in real life? Examples of axioms of. Group Ring Examples.
From www.scoreexchange.com
Helpsheet More About Grouping Notes Together Sheet Music PDF file Group Ring Examples R, together with two binary operations, denoted by +. Is associative, i.e., (a · b) · c =. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. (r,+) is an abelian group.. Group Ring Examples.
From classroomsecrets.co.uk
Sharing and Grouping Varied Fluency Classroom Secrets Classroom Group Ring Examples Ring (r,+,·) is a set and · , such that: M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Rotations of objects, symmetries in physics. What are some examples of groups, rings, and fields in real life? (r,+) is an abelian group. Informal definitions a group is a set in which you can perform one operation (usually. Group Ring Examples.
From kmr.dialectica.se
Group, Ring, Field, Module, Vector Space Knowledge Management Group Ring Examples What are some examples of groups, rings, and fields in real life? R, together with two binary operations, denoted by +. Rotations of objects, symmetries in physics. (r,+) is an abelian group. Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. Is associative, i.e., (a · b) ·. Group Ring Examples.
From www.youtube.com
Maths grouping and sharing practice YouTube Group Ring Examples Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. R, together with two binary operations, denoted by +. (r,+) is an abelian group. A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for. Group Ring Examples.
From www.slideserve.com
PPT PART I Symmetric Ciphers CHAPTER 4 Finite Fields 4.1 Groups Group Ring Examples Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. Is associative, i.e., (a · b) · c =. Rotations of objects, symmetries in physics. R, together with two binary operations, denoted by +. Informal definitions a. Group Ring Examples.
From calcworkshop.com
How to Factor by Grouping? (15+ Amazing Examples!) Group Ring Examples (r,+) is an abelian group. Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. Rotations of objects, symmetries in physics. Ring (r,+,·) is. Group Ring Examples.
From www.youtube.com
Group/Ring theory what is ring ring definition/Properties ring Group Ring Examples Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. R, together with two binary operations, denoted by +. Ring (r,+,·) is a set and · , such that: M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. A ring (with identity) is a set r. Group Ring Examples.
From github.com
GitHub pep1024/grouping_examples Examples of grouping a continuous Group Ring Examples M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. (r,+) is an abelian group. Rotations of objects, symmetries in physics. Ring (r,+,·) is a set and · , such that: A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; Informal definitions a group is. Group Ring Examples.
From www.youtube.com
Factoring by Grouping Factoring Polynomials YouTube Group Ring Examples Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. (r,+) is an abelian group. What are some examples of groups, rings, and fields in real life? Rotations of objects, symmetries in physics. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for.. Group Ring Examples.
From www.youtube.com
Group & Ring 1 Group and It's Properties Group Theory Algebraic Group Ring Examples Ring (r,+,·) is a set and · , such that: R, together with two binary operations, denoted by +. Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. Examples of axioms of type (∀) for r are commutativity and associativity of both + and. Group Ring Examples.
From www.slideserve.com
PPT Perception PowerPoint Presentation, free download ID1432134 Group Ring Examples What are some examples of groups, rings, and fields in real life? R, together with two binary operations, denoted by +. Examples of axioms of type (∀) for r are commutativity and associativity of both + and ·, and the distributive law. Is associative, i.e., (a · b) · c =. Ring (r,+,·) is a set and · , such. Group Ring Examples.
From blog.logrocket.com
What is affinity grouping? Definition, examples, and howto LogRocket Group Ring Examples Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. (r,+) is an abelian group. Ring (r,+,·) is a set and · , such that: R, together with two binary operations, denoted by. Group Ring Examples.
From maze.co
A Guide to Gestalt Grouping Principles of Design Maze Group Ring Examples Informal definitions a group is a set in which you can perform one operation (usually addition or multiplication mod n for us) with some nice. A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; Is associative, i.e., (a · b) · c =. M1 → m2 of. Group Ring Examples.
From medium.com
Group, Ring, Integral Domain and Field Theory A Gentle Introduction Group Ring Examples A ring (with identity) is a set r together with two binary operations + and (called addition and multiplication), where for a; Is associative, i.e., (a · b) · c =. Rotations of objects, symmetries in physics. R, together with two binary operations, denoted by +. M1 → m2 of abelian groups such that α(rm1) = rα(m1) for. (r,+) is. Group Ring Examples.