Cylindrical Function . The behavior goes from power law. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. A thoughtful choice of coordinate system. (1) the bessel functions are. These jν(x) are called cylindrical bessel functions. Behavior near the origin and far away:
from www.chegg.com
The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Behavior near the origin and far away: Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). (1) the bessel functions are. A thoughtful choice of coordinate system. The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. These jν(x) are called cylindrical bessel functions. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The behavior goes from power law.
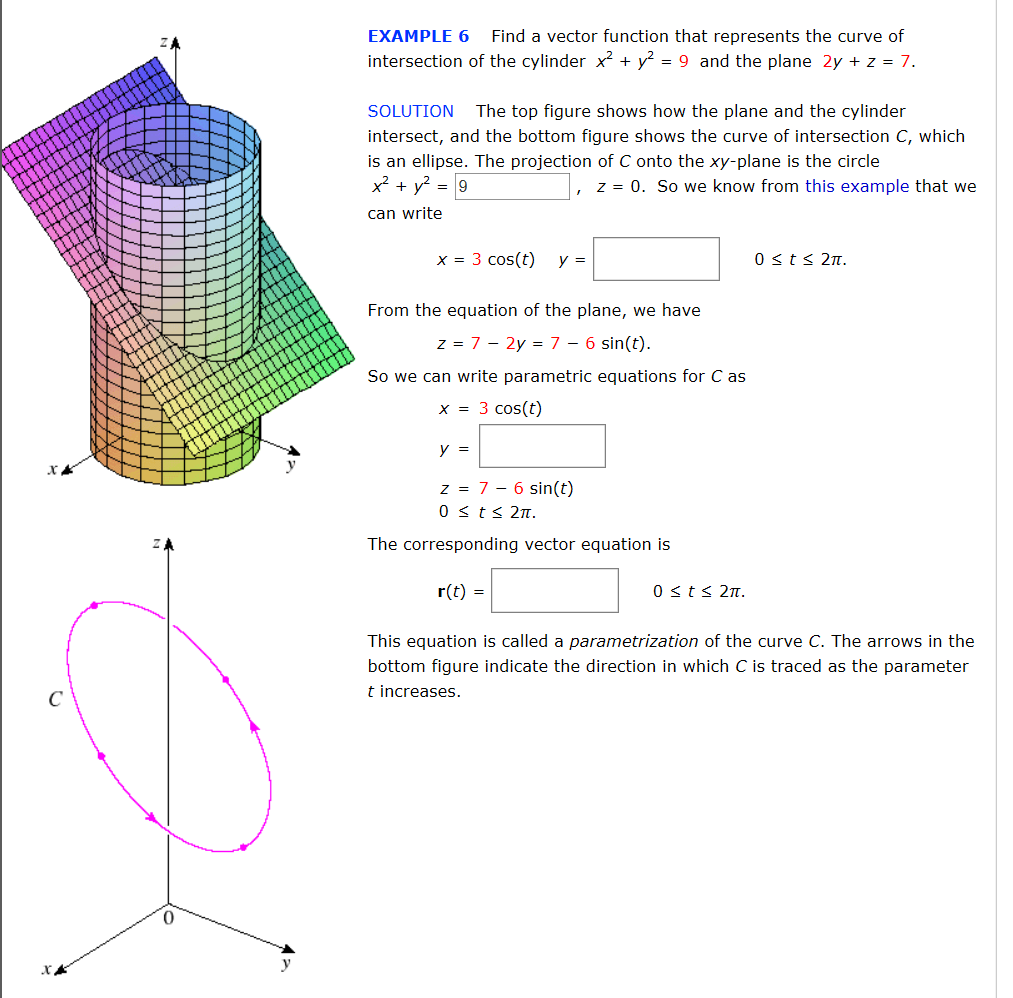
Solved EXAMPLE 6 Find a vector function that represents the
Cylindrical Function These jν(x) are called cylindrical bessel functions. The behavior goes from power law. A thoughtful choice of coordinate system. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). These jν(x) are called cylindrical bessel functions. The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. (1) the bessel functions are. Behavior near the origin and far away:
From www.researchgate.net
Cylindrical Bessel functions of different orders. The horizontal axis Cylindrical Function The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; The behavior goes from power law. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4).. Cylindrical Function.
From owlcation.com
Cylindrical Coordinates Rectangular to Cylindrical Coordinates Cylindrical Function (1) the bessel functions are. These jν(x) are called cylindrical bessel functions. The behavior goes from power law. Behavior near the origin and far away: Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). Cylindrical and spherical coordinates give us the flexibility to select a coordinate system. Cylindrical Function.
From www.chegg.com
Solved EXAMPLE 6 Find a vector function that represents the Cylindrical Function The behavior goes from power law. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. These jν(x) are called cylindrical bessel functions. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). The function w(z;t) is called the. Cylindrical Function.
From www.youtube.com
Fluid Mechanics Lesson 10D Stream Function, Cylindrical Coordinates Cylindrical Function The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Behavior near the origin and far away: The behavior goes from power law. The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. (1) the bessel functions are. Cylindrical and spherical coordinates give us the flexibility to select. Cylindrical Function.
From curvebreakerstestprep.com
Surface Area of a Cylinder Formula & Examples Curvebreakers Cylindrical Function Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. A thoughtful choice of coordinate system. The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. Behavior near the origin and far away: (1) the bessel functions are.. Cylindrical Function.
From www.slideserve.com
PPT Cylindrical and Spherical Coordinates PowerPoint Presentation Cylindrical Function The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. Behavior near the origin and far away: Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). The behavior goes from power law. A thoughtful. Cylindrical Function.
From www.phys.ksu.edu
Electrodynamics I, KSU Physics Cylindrical Function The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). A thoughtful choice of coordinate system. Behavior near the origin and far away: Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the. Cylindrical Function.
From ximera.osu.edu
Cylindrical Coordinates Ximera Cylindrical Function A thoughtful choice of coordinate system. (1) the bessel functions are. Behavior near the origin and far away: Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The behavior goes from power law. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x −. Cylindrical Function.
From www.cuemath.com
Cylinder Shape, Formula, Examples Faces Vertices Edges Cylindrical Function Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). (1) the bessel functions are. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. A thoughtful choice of coordinate system. These jν(x) are called cylindrical bessel functions. The. Cylindrical Function.
From www.chegg.com
Solved Direction of Current I . A long, cylindrical Cylindrical Function The behavior goes from power law. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. A thoughtful choice of coordinate system. The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. (1) the bessel functions are. The. Cylindrical Function.
From www.youtube.com
Separation of Variables Cylindrical Coordinates (Part 2) YouTube Cylindrical Function Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The behavior goes from power law. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. Behavior near the. Cylindrical Function.
From www.slideserve.com
PPT Chapter 9 Differential Analysis of Fluid Flow PowerPoint Cylindrical Function (1) the bessel functions are. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; These jν(x) are called cylindrical bessel functions. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 −. Cylindrical Function.
From www.researchgate.net
Illustration of steps leading from cylindrical functions of edge Cylindrical Function (1) the bessel functions are. The behavior goes from power law. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). These jν(x) are called cylindrical bessel functions. The function w(z;t) is called the generating function of the bessel. Cylindrical Function.
From ximera.osu.edu
Cylindrical Coordinates Ximera Cylindrical Function These jν(x) are called cylindrical bessel functions. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; A thoughtful choice of coordinate system. The behavior goes from power law. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). The function w(z;t) is called the generating function of the. Cylindrical Function.
From www.chegg.com
Solved Problem 1 Div and Curl in Cylindrical Coordinates (6 Cylindrical Function Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. Behavior near the origin and far away: Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). (1) the bessel functions are. The cylinder function is defined as c(x,y)={1. Cylindrical Function.
From www.youtube.com
Math 212 GH Lecture 23 Equations of Lines and Planes; Sketching Cylindrical Function The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. A thoughtful choice of coordinate system. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). These jν(x) are called cylindrical bessel functions. The behavior. Cylindrical Function.
From quizlet.com
Sketch graphs of the cylindrical equations. r=4 Quizlet Cylindrical Function Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). These jν(x) are called cylindrical bessel functions. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Behavior near the origin and far away: Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to. Cylindrical Function.
From www.youtube.com
Separation of Variables Cylindrical Coordinates (Part 1) YouTube Cylindrical Function A thoughtful choice of coordinate system. Behavior near the origin and far away: The behavior goes from power law. The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. These jν(x) are called cylindrical bessel functions. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Jν(x) =. Cylindrical Function.
From www.slideserve.com
PPT HW/Tutorial 1 WWWR Chapters 1516 ID Chapters 12 PowerPoint Cylindrical Function Behavior near the origin and far away: The behavior goes from power law. These jν(x) are called cylindrical bessel functions. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). (1) the bessel functions are. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system. Cylindrical Function.
From www.cuemath.com
Volume of a Cylinder Formula How to Find Volume of Cylinder? Cylindrical Function The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Jν(x) = 1 γ (ν + 1) (x 2)ν. Cylindrical Function.
From handwiki.org
Parabolic cylinder function HandWiki Cylindrical Function Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; The function w(z;t) is called the generating function of the. Cylindrical Function.
From www.chegg.com
Solved solve the infinite cylindrical well, with radius a Cylindrical Function These jν(x) are called cylindrical bessel functions. Behavior near the origin and far away: The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. (1) the bessel functions are. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) →. Cylindrical Function.
From www.youtube.com
cylindrical coordinate system YouTube Cylindrical Function Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. Behavior near the origin and far away: The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. These jν(x) are called cylindrical bessel functions. (1) the bessel functions. Cylindrical Function.
From study.com
Cylindrical & Spherical Coordinates Conversion & Examples Lesson Cylindrical Function The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). Behavior near the origin and far away: The behavior goes from power law. These jν(x) are called cylindrical bessel functions. (1) the bessel functions are. The function w(z;t) is. Cylindrical Function.
From octave.sourceforge.io
Function Reference cylinder Cylindrical Function Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. A thoughtful choice of coordinate system. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; Behavior near the origin. Cylindrical Function.
From sites.und.edu
14.7 Triple Integration with Cylindrical and Spherical Coordinates Cylindrical Function The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. These jν(x) are called cylindrical bessel functions. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). Cylindrical and spherical coordinates give us the flexibility. Cylindrical Function.
From www.researchgate.net
Top cylindrical harmonics cos(lϕ), sin(lϕ) in polar coordinates r Cylindrical Function The behavior goes from power law. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). A thoughtful choice of coordinate system. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The cylinder function is defined as c(x,y)={1. Cylindrical Function.
From www.nagwa.com
Question Video Interpreting and Factoring the Expression for the Cylindrical Function The behavior goes from power law. (1) the bessel functions are. A thoughtful choice of coordinate system. The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯,. Cylindrical Function.
From engcourses-uofa.ca
Engineering at Alberta Courses » Vector Calculus in Cylindrical Cylindrical Function (1) the bessel functions are. A thoughtful choice of coordinate system. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). These jν(x) are called cylindrical bessel functions. Behavior near the origin and far away: Cylindrical and spherical coordinates give us the flexibility to select a coordinate system. Cylindrical Function.
From www.researchgate.net
Cylindrical coordinates and directions as used in our derivations Cylindrical Function Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. A thoughtful choice of coordinate system. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). Behavior near the origin and far away: The behavior goes from power law.. Cylindrical Function.
From www.youtube.com
Heat Transfer Chapter 2 Example Problem 6 Solving the Heat Cylindrical Function Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). (1) the bessel functions are. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. These jν(x) are called cylindrical bessel functions. The function w(z;t) is called the generating. Cylindrical Function.
From scienceforyou.netlify.app
Graduated cylinder function scienceforyou Cylindrical Function Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). These jν(x) are called cylindrical bessel functions. The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. (1) the bessel functions are. Cylindrical and spherical. Cylindrical Function.
From www.geogebra.org
Cylindrical Coordinates GeoGebra Cylindrical Function These jν(x) are called cylindrical bessel functions. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. (1) the bessel functions are. Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). Behavior near the origin and far away:. Cylindrical Function.
From www.chegg.com
Solved Use cylindrical coordinates to calculate SI DHE f(x, Cylindrical Function Jν(x) = 1 γ (ν + 1) (x 2)ν + ⋯, jν(x) → √ 2 πxcos(x − νπ 2 − π 4). These jν(x) are called cylindrical bessel functions. A thoughtful choice of coordinate system. The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an important role in. The cylinder. Cylindrical Function.
From www.researchgate.net
Illustration of steps leading from cylindrical functions of edge Cylindrical Function The cylinder function is defined as c(x,y)={1 for sqrt(x^2+y^2)<=<strong>a</strong>; These jν(x) are called cylindrical bessel functions. A thoughtful choice of coordinate system. (1) the bessel functions are. The behavior goes from power law. Behavior near the origin and far away: The function w(z;t) is called the generating function of the bessel functions of integer order, and formula (b.26) plays an. Cylindrical Function.