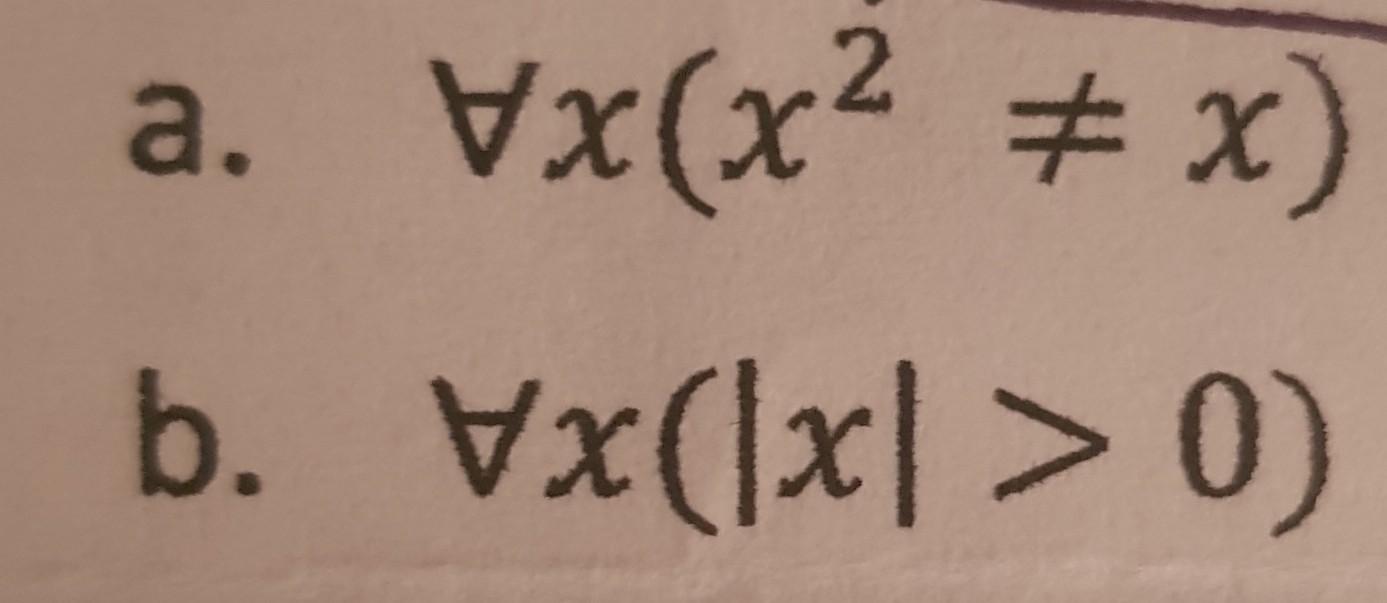Discrete Math Counterexample . In this chapter, we introduce the notion of proof in mathematics. To give a counterexample, i. Chapter 4.2 direct proof and counterexample 2: For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Since so many statements in mathematics are. 1 what is a contrapositive? \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Give a counterexample to show the following statement is false: Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false Direct proof and counterexample 1. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. We do 2 things in our.
from www.chegg.com
Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false \if p then q is logically equivalent to \if not q then not p our goal is to get to the. 1 what is a contrapositive? Since so many statements in mathematics are. To give a counterexample, i. Direct proof and counterexample 1. We do 2 things in our. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. In this chapter, we introduce the notion of proof in mathematics. Chapter 4.2 direct proof and counterexample 2:
Solved Discrete Math Find a counterexample, if available, to
Discrete Math Counterexample We do 2 things in our. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. Since so many statements in mathematics are. We do 2 things in our. In this chapter, we introduce the notion of proof in mathematics. Give a counterexample to show the following statement is false: Chapter 4.2 direct proof and counterexample 2: \if p then q is logically equivalent to \if not q then not p our goal is to get to the. To give a counterexample, i. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false Direct proof and counterexample 1. 1 what is a contrapositive? For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most.
From calcworkshop.com
Direct Proof (Explained w/ 11+ StepbyStep Examples!) Discrete Math Counterexample Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. In this chapter, we introduce the notion of proof in mathematics. Since so many statements in mathematics are. Chapter 4.2 direct proof and counterexample 2: Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such. Discrete Math Counterexample.
From www.slideserve.com
PPT Introduction to Discrete Mathematics PowerPoint Presentation Discrete Math Counterexample Give a counterexample to show the following statement is false: We do 2 things in our. 1 what is a contrapositive? For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. To give a counterexample, i. In this chapter, we introduce the notion of proof in mathematics. Since so many statements in mathematics are. Direct proof and. Discrete Math Counterexample.
From www.slideserve.com
PPT Discrete Mathematics Lecture 3 Elementary Number Theory and Discrete Math Counterexample In this chapter, we introduce the notion of proof in mathematics. To give a counterexample, i. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Chapter 4.2 direct proof and counterexample 2: \if. Discrete Math Counterexample.
From www.scribd.com
Mod 4 Up Down Counter Discrete Mathematics Electronic Engineering Discrete Math Counterexample In this chapter, we introduce the notion of proof in mathematics. Since so many statements in mathematics are. To give a counterexample, i. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. Chapter 4.2 direct proof and counterexample 2: We do 2 things in our. For. Discrete Math Counterexample.
From www.chegg.com
Solved ds22017Winter 2017 MATH240001 Discrete Structures Discrete Math Counterexample Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. \if p then q is logically equivalent to \if not q then not p our goal is to get to the. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Since so many. Discrete Math Counterexample.
From study.com
How to Identify Counterexamples in Algebra Algebra Discrete Math Counterexample Give a counterexample to show the following statement is false: \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Chapter 4.2 direct proof and counterexample 2: Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false For all. Discrete Math Counterexample.
From math.stackexchange.com
Discrete math proofverification of divisibility. Case with both truth Discrete Math Counterexample We do 2 things in our. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false \if p then q is logically equivalent to \if not q then not p our goal is to get to the. To give a counterexample, i. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then. Discrete Math Counterexample.
From www.studocu.com
Discrete Structures Section 6 Section 6 Counterexample Statement Discrete Math Counterexample Direct proof and counterexample 1. Since so many statements in mathematics are. Chapter 4.2 direct proof and counterexample 2: In this chapter, we introduce the notion of proof in mathematics. 1 what is a contrapositive? \if p then q is logically equivalent to \if not q then not p our goal is to get to the. We do 2 things. Discrete Math Counterexample.
From www.studocu.com
Intro To Discrete Math Proof by Smallest Counterexample Proof by Discrete Math Counterexample \if p then q is logically equivalent to \if not q then not p our goal is to get to the. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false Since so many statements in mathematics. Discrete Math Counterexample.
From www.youtube.com
Proof by Smallest Counterexample YouTube Discrete Math Counterexample Since so many statements in mathematics are. Give a counterexample to show the following statement is false: We do 2 things in our. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Direct proof and counterexample 1. \if p then q is logically equivalent to \if not q then not p our goal is to get. Discrete Math Counterexample.
From www.youtube.com
DISCRETE MATHEMATICS CLASS25 Universal Quantifiers Counter Discrete Math Counterexample Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. Chapter 4.2 direct proof and counterexample 2: In this chapter, we introduce the notion of proof in mathematics. Direct proof and counterexample 1. Give a counterexample to show the following statement is false: To give a counterexample,. Discrete Math Counterexample.
From www.slideserve.com
PPT Discrete Mathematics PowerPoint Presentation, free download ID Discrete Math Counterexample Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. In this chapter, we introduce the notion of proof in mathematics. Since so many statements in mathematics are. 1 what is a contrapositive? Chapter 4.2 direct proof and counterexample 2: Give a counterexample to show the following. Discrete Math Counterexample.
From www.youtube.com
Universal quantifier counterexample in discrete math(1.4) اردو / हिंदी Discrete Math Counterexample Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. We do 2 things in our. 1 what is a contrapositive? \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Relative to the logical implication. Discrete Math Counterexample.
From www.numerade.com
SOLVED provide counterexample. discrete math (d) For every positive Discrete Math Counterexample Direct proof and counterexample 1. We do 2 things in our. Chapter 4.2 direct proof and counterexample 2: To give a counterexample, i. 1 what is a contrapositive? For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. In this chapter, we introduce the notion of proof in mathematics. Give a counterexample to show the following statement. Discrete Math Counterexample.
From www.cs.tulane.edu
CMPS/MATH 2170 Discrete Mathematics Slides, pictures Discrete Math Counterexample \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Give a counterexample to show the following statement is false: Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\). Discrete Math Counterexample.
From exoxkrobm.blob.core.windows.net
Proof By Counterexample Discrete Math at Sidney Bergeron blog Discrete Math Counterexample Direct proof and counterexample 1. \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false In this chapter, we introduce the notion of proof in mathematics. To give a. Discrete Math Counterexample.
From hxeokjinj.blob.core.windows.net
Discrete Mathematics Counter Example at Frank Rivera blog Discrete Math Counterexample \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. Chapter 4.2 direct proof and counterexample 2: 1 what is a contrapositive? For all \(a, b\in. Discrete Math Counterexample.
From slideplayer.com
MAT 2720 Discrete Mathematics ppt download Discrete Math Counterexample 1 what is a contrapositive? To give a counterexample, i. \if p then q is logically equivalent to \if not q then not p our goal is to get to the. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Direct proof and counterexample 1. Give a counterexample to show the following statement is false: Relative. Discrete Math Counterexample.
From www.youtube.com
Counterexample in Discrete Mathematics with Example YouTube Discrete Math Counterexample 1 what is a contrapositive? Give a counterexample to show the following statement is false: In this chapter, we introduce the notion of proof in mathematics. To give a counterexample, i. \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Since so many statements in mathematics are. Chapter. Discrete Math Counterexample.
From www.youtube.com
Discrete Math 1 Tutorial 41 Quantifiers, Negation and Examples Discrete Math Counterexample For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Direct proof and counterexample 1. Give a counterexample to show the following statement is false: Since so many statements in mathematics are. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. Chapter 4.2. Discrete Math Counterexample.
From www.docsity.com
Counterexample Honors Discrete Mathematics Note 5 MAD 2104 Docsity Discrete Math Counterexample Direct proof and counterexample 1. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Since so many statements in mathematics are. We do 2 things in our. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. Relative to the logical implication \(p. Discrete Math Counterexample.
From www.slideserve.com
PPT 22C19 Discrete Math Logic and Proof PowerPoint Presentation Discrete Math Counterexample Since so many statements in mathematics are. Give a counterexample to show the following statement is false: Direct proof and counterexample 1. To give a counterexample, i. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement. Discrete Math Counterexample.
From www.chegg.com
Solved Discrete Math Find a counterexample, if available, to Discrete Math Counterexample Chapter 4.2 direct proof and counterexample 2: To give a counterexample, i. Direct proof and counterexample 1. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”.. Discrete Math Counterexample.
From www.studocu.com
CSE 173 Counting counter Discrete Mathematics Studocu Discrete Math Counterexample For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. We do 2 things in our. Give a counterexample to show the following statement is false: Chapter 4.2 direct proof and counterexample 2: Direct proof and counterexample 1. Since so many statements in mathematics are. To give a counterexample, i. In this chapter, we introduce the notion. Discrete Math Counterexample.
From www.slideserve.com
PPT Discrete Structures Introduction to Proofs PowerPoint Discrete Math Counterexample Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. We do 2 things in our. \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement. Discrete Math Counterexample.
From math.stackexchange.com
discrete mathematics Proof by Smallest counterexample for integers Discrete Math Counterexample Give a counterexample to show the following statement is false: Since so many statements in mathematics are. To give a counterexample, i. 1 what is a contrapositive? \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Give a counterexample to the statement “if n is an integer and. Discrete Math Counterexample.
From www.lisbonlx.com
Discrete Math Tutorial Examples and Forms Discrete Math Counterexample 1 what is a contrapositive? To give a counterexample, i. We do 2 things in our. Direct proof and counterexample 1. Chapter 4.2 direct proof and counterexample 2: In this chapter, we introduce the notion of proof in mathematics. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false Give. Discrete Math Counterexample.
From www.slideserve.com
PPT CSE115/ENGR160 Discrete Mathematics 02/01/11 PowerPoint Discrete Math Counterexample Chapter 4.2 direct proof and counterexample 2: For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Direct proof and counterexample 1. In this chapter, we introduce the notion of proof in mathematics. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false \if p then q. Discrete Math Counterexample.
From www.slideserve.com
PPT Discrete Maths PowerPoint Presentation, free download ID1967699 Discrete Math Counterexample We do 2 things in our. Chapter 4.2 direct proof and counterexample 2: In this chapter, we introduce the notion of proof in mathematics. To give a counterexample, i. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Since so many statements in mathematics are. \if p then q is logically equivalent to \if not q. Discrete Math Counterexample.
From slideplayer.com
Direct Proof and Counterexample I ppt download Discrete Math Counterexample Direct proof and counterexample 1. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. Give a counterexample to show the following statement is false: For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Relative to the logical implication \(p \rightarrow q\text{,}\) a. Discrete Math Counterexample.
From www.cuemath.com
Counterexample Cuemath Discrete Math Counterexample Give a counterexample to show the following statement is false: For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. We do 2 things in our. Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”. 1 what is a contrapositive? Relative to the. Discrete Math Counterexample.
From exoxkrobm.blob.core.windows.net
Proof By Counterexample Discrete Math at Sidney Bergeron blog Discrete Math Counterexample Chapter 4.2 direct proof and counterexample 2: Direct proof and counterexample 1. To give a counterexample, i. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false Give a counterexample to the statement “if n is an integer and n2 is divisible by 4, then n is divisible by 4.”.. Discrete Math Counterexample.
From www.slideserve.com
PPT CS201 Data Structures and Discrete Mathematics I PowerPoint Discrete Math Counterexample Direct proof and counterexample 1. For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Since so many statements in mathematics are. Chapter 4.2 direct proof and counterexample 2: 1 what is a contrapositive? In this chapter, we introduce the notion of proof in mathematics. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such. Discrete Math Counterexample.
From www.slideserve.com
PPT Discrete Mathematics Lecture 3 Elementary Number Theory and Discrete Math Counterexample For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. \if p then q is logically equivalent to \if not q then not p our goal is to get to the. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false We do 2 things in our.. Discrete Math Counterexample.
From www.youtube.com
Discrete Math 25Methods of Proof Direct Proof Disproof by counter Discrete Math Counterexample We do 2 things in our. 1 what is a contrapositive? Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false For all \(a, b\in \mathbb{r}\) if \(a^2=b^2\) then \(a=b\text{.}\) one of the most. Direct proof and counterexample 1. Give a counterexample to show the following statement is false: To. Discrete Math Counterexample.