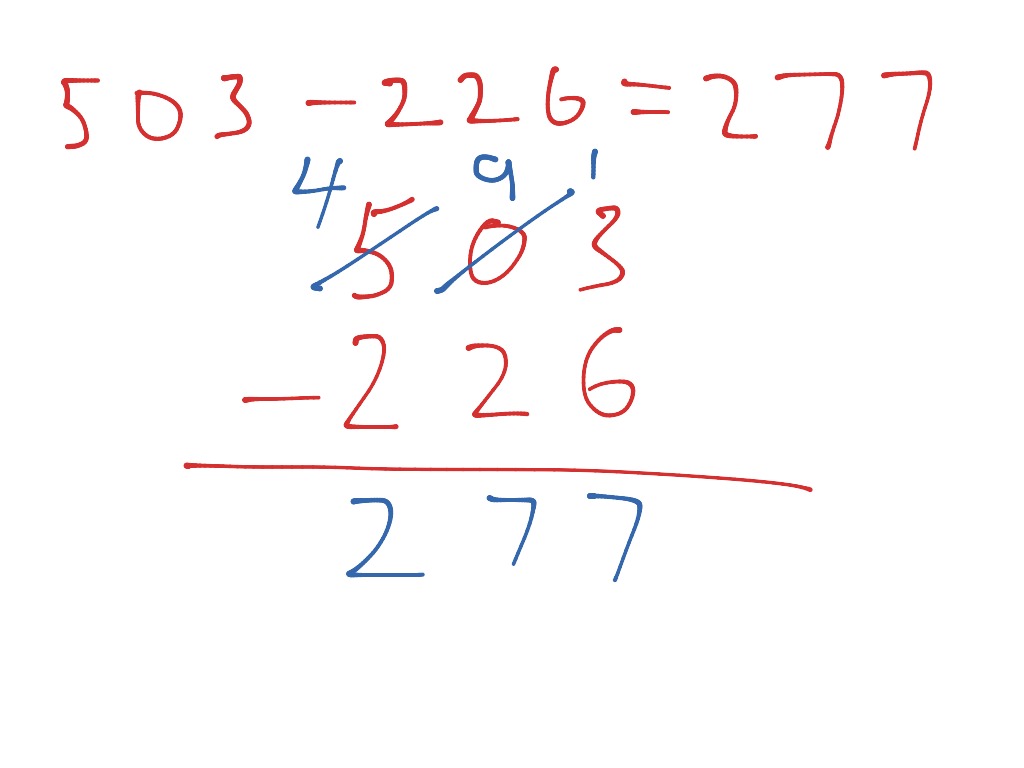What Does Compact Mean In Math . compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. Closed bounded sets in $\mathbb{r}^n$ are compact. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. the discrete metric space on a finite set is compact. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite.
from www.showme.com
the discrete metric space on a finite set is compact. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. Closed bounded sets in $\mathbb{r}^n$ are compact.
Subtraction using the compact column method Math ShowMe
What Does Compact Mean In Math the discrete metric space on a finite set is compact. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. the discrete metric space on a finite set is compact. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. Closed bounded sets in $\mathbb{r}^n$ are compact. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do.
From www.youtube.com
Continuous Function from Compact Set is Uniformly Continuous Math What Does Compact Mean In Math in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. compactness = any equation that can be approximated by a consistent system of ≤. What Does Compact Mean In Math.
From www.scribd.com
Mathematics Real Analysys Compact Examples PDF What Does Compact Mean In Math what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. the compactness of a metric space is defined as, let (x, d) be a metric space. What Does Compact Mean In Math.
From www.showme.com
Subtraction using the compact column method Math ShowMe What Does Compact Mean In Math the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. Closed bounded sets in $\mathbb{r}^n$ are compact. compactness = any equation that can be approximated by a. What Does Compact Mean In Math.
From www.studocu.com
Introduction to compact sets In compact spaces, the following What Does Compact Mean In Math the discrete metric space on a finite set is compact. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. compactness is a topological property that is fundamental. What Does Compact Mean In Math.
From www.showme.com
Compact Column Subtraction WEJS Year 5&6 Math ShowMe What Does Compact Mean In Math compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. what compactness does for us is allow us to turn in nite collections of. What Does Compact Mean In Math.
From math.stackexchange.com
compactness How to prove a set of sequences is compact? Mathematics What Does Compact Mean In Math in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite.. What Does Compact Mean In Math.
From www.slideserve.com
PPT Math 2999 presentation PowerPoint Presentation, free download What Does Compact Mean In Math what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. compactness is a topological property that is. What Does Compact Mean In Math.
From www.youtube.com
Expanded and Compact Forms YouTube What Does Compact Mean In Math the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that.. What Does Compact Mean In Math.
From kellyhaskins.weebly.com
Compact Math Mrs. Haskins What Does Compact Mean In Math the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. the discrete metric space on a finite set is compact. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. what compactness does. What Does Compact Mean In Math.
From www.youtube.com
Mathematics What does it mean by a relatively compact open set? YouTube What Does Compact Mean In Math compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of. What Does Compact Mean In Math.
From exoxlulfo.blob.core.windows.net
What Is Compact Set Mean at John Wunder blog What Does Compact Mean In Math the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical.. What Does Compact Mean In Math.
From kellyhaskins.weebly.com
Compact Math Mrs. Haskins What Does Compact Mean In Math the discrete metric space on a finite set is compact. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness = any equation that. What Does Compact Mean In Math.
From xsquared.net
Union of open subsets in a compact space math questions, answers What Does Compact Mean In Math compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. what compactness does for us. What Does Compact Mean In Math.
From www.showme.com
Compact multiplication Math ShowMe What Does Compact Mean In Math the discrete metric space on a finite set is compact. Closed bounded sets in $\mathbb{r}^n$ are compact. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. the compactness of a metric space is defined as, let (x, d) be a metric space. What Does Compact Mean In Math.
From www.youtube.com
Real valued Continuous function on Compact set Analysis BSc What Does Compact Mean In Math the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness = any equation that can be. What Does Compact Mean In Math.
From math.stackexchange.com
real analysis Bounded, closed \implies compact Mathematics Stack What Does Compact Mean In Math the discrete metric space on a finite set is compact. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness, in mathematics, property of some topological spaces (a generalization of euclidean. What Does Compact Mean In Math.
From math.stackexchange.com
general topology Determining if following sets are closed, open, or What Does Compact Mean In Math in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of. What Does Compact Mean In Math.
From www.studypool.com
SOLUTION Mathematics real analysis compact examples Studypool What Does Compact Mean In Math in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of. What Does Compact Mean In Math.
From math.stackexchange.com
real analysis Help understanding proof involving smooth functions of What Does Compact Mean In Math what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. Closed bounded sets in $\mathbb{r}^n$ are compact. compactness, in mathematics, property of some topological spaces (a. What Does Compact Mean In Math.
From www.studypool.com
SOLUTION Mathematics real analysis compact examples Studypool What Does Compact Mean In Math compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x. What Does Compact Mean In Math.
From studylib.net
Continuous functions on compact sets. What Does Compact Mean In Math what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. compactness = any equation that can be. What Does Compact Mean In Math.
From www.showme.com
Addition using compact method Math, 2nd Grade Math, 2.OA.3 ShowMe What Does Compact Mean In Math in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of. What Does Compact Mean In Math.
From www.showme.com
Compact Subtraction with 0 Math ShowMe What Does Compact Mean In Math what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. the. What Does Compact Mean In Math.
From math.stackexchange.com
general topology Which of the following are compact sets What Does Compact Mean In Math what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset. What Does Compact Mean In Math.
From www.showme.com
Multiplication Compact Method TUXTU Math, Arithmetic What Does Compact Mean In Math Closed bounded sets in $\mathbb{r}^n$ are compact. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. compactness is a topological property that. What Does Compact Mean In Math.
From www.showme.com
Compact Method Addition Math ShowMe What Does Compact Mean In Math compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. in mathematics, specifically general topology, compactness is a property that generalizes the notion. What Does Compact Mean In Math.
From www.youtube.com
Closed subset of a compact set is compact Compact set Real analysis What Does Compact Mean In Math in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that. What Does Compact Mean In Math.
From www.showme.com
Compact Multiplication Method 1 Math, Arithmetic, multiplication ShowMe What Does Compact Mean In Math in mathematics, specifically general topology, compactness is a property that generalizes the notion of a subset of. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. the discrete metric space on a finite set is compact. compactness, in mathematics, property of some topological spaces (a generalization of euclidean. What Does Compact Mean In Math.
From lessoncampusthomas.z19.web.core.windows.net
Compact Form In Math What Does Compact Mean In Math what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. Closed bounded sets in $\mathbb{r}^n$ are compact. the discrete metric space on a finite set is. What Does Compact Mean In Math.
From materialfullcrenated.z13.web.core.windows.net
What Is Compact In Math What Does Compact Mean In Math Closed bounded sets in $\mathbb{r}^n$ are compact. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. the discrete metric space on a finite set is compact. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. the compactness of a metric space is defined. What Does Compact Mean In Math.
From in.pinterest.com
Compact Mathematics for classes 1 to 5 What Does Compact Mean In Math the discrete metric space on a finite set is compact. what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. compactness, in. What Does Compact Mean In Math.
From www.youtube.com
Distance Between Compact Sets Math Notes for the Curious YouTube What Does Compact Mean In Math compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite.. What Does Compact Mean In Math.
From math.stackexchange.com
general topology Visual representation of difference between closed What Does Compact Mean In Math compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. compactness, in mathematics, property of some topological spaces (a generalization of euclidean space) that. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. in mathematics, specifically general topology,. What Does Compact Mean In Math.
From www.researchgate.net
(PDF) A Characterization of Compact Operators by Orthogonality What Does Compact Mean In Math what compactness does for us is allow us to turn in nite collections of open sets into nite collections of open sets that do. compactness = any equation that can be approximated by a consistent system of ≤ inequalities of continuous functions has a. compactness is a topological property that is fundamental in real analysis, algebraic geometry,. What Does Compact Mean In Math.
From www.docsity.com
Exercises on Compact and Connected Subsets in R Assignment MATH 381 What Does Compact Mean In Math compactness is a topological property that is fundamental in real analysis, algebraic geometry, and many other mathematical. the discrete metric space on a finite set is compact. the compactness of a metric space is defined as, let (x, d) be a metric space such that every open cover of x has a finite. Closed bounded sets in. What Does Compact Mean In Math.