Equation Cone Coordinates at Isabel Spiegel blog

Equation Cone Coordinates. In cylindrical coordinates, a cone can be represented by equation \(z=kr,\) where \(k\) is a constant. Conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). Guide curve of a cone is a curve, which describes the. If the plane is parallel to the. A (finite, circular) conical surface is a ruled surface created by fixing one end of a line segment at a point (known as the vertex or apex. Lateral height of right circular cone in terms of radius r and height h (by the pythagorean theorem): X2 a2 + y2 b2 = z2 c2 x 2 a 2 + y 2 b 2 = z 2 c 2. Here is a sketch of a typical cone. L = √ r2 + h2. There are three major sections of a cone or conic sections: Now, note that while we called this a cone it is more. Here is the general equation of a cone. Conic sections or sections of a cone are the curves obtained by the intersection of a plane and cone. I usually use the following parametric equation to find the surface area of a regular cone $z=\sqrt{x^2+y^2}$:

In cylindrical coordinates, a cone can be represented by equation \(z=kr,\) where \(k\) is a constant. Here is a sketch of a typical cone. X2 a2 + y2 b2 = z2 c2 x 2 a 2 + y 2 b 2 = z 2 c 2. Conic sections or sections of a cone are the curves obtained by the intersection of a plane and cone. L = √ r2 + h2. If the plane is parallel to the. Lateral height of right circular cone in terms of radius r and height h (by the pythagorean theorem): I usually use the following parametric equation to find the surface area of a regular cone $z=\sqrt{x^2+y^2}$: There are three major sections of a cone or conic sections: A (finite, circular) conical surface is a ruled surface created by fixing one end of a line segment at a point (known as the vertex or apex.

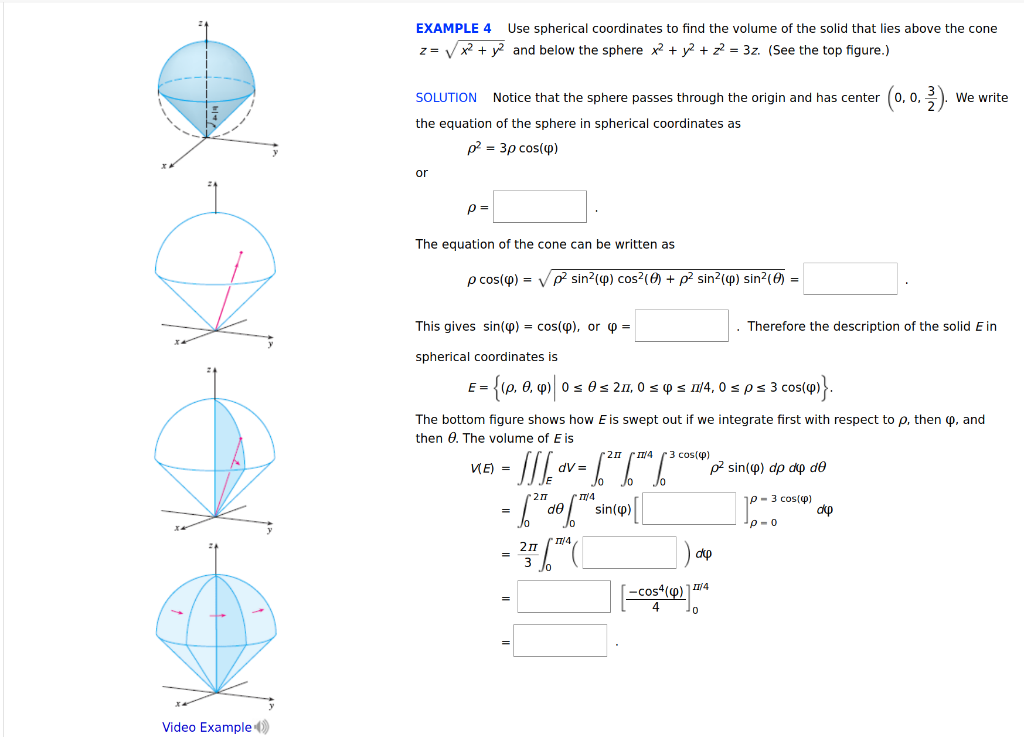
Solved EXAMPLE 4 Use spherical coordinates to find the

Equation Cone Coordinates Here is the general equation of a cone. A (finite, circular) conical surface is a ruled surface created by fixing one end of a line segment at a point (known as the vertex or apex. Now, note that while we called this a cone it is more. Conic sections or sections of a cone are the curves obtained by the intersection of a plane and cone. X2 a2 + y2 b2 = z2 c2 x 2 a 2 + y 2 b 2 = z 2 c 2. There are three major sections of a cone or conic sections: If the plane is parallel to the. Here is a sketch of a typical cone. I usually use the following parametric equation to find the surface area of a regular cone $z=\sqrt{x^2+y^2}$: Guide curve of a cone is a curve, which describes the. In cylindrical coordinates, a cone can be represented by equation \(z=kr,\) where \(k\) is a constant. Lateral height of right circular cone in terms of radius r and height h (by the pythagorean theorem): Conic sections are generated by the intersection of a plane with a cone (figure \ (\pageindex {2}\)). L = √ r2 + h2. Here is the general equation of a cone.