Differential Geometry Vs Euclidean . The study concerns properties of sufficiently small pieces of them. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. Descartes discovered that these types of geometries could be described by. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. We have explained there how the geodesics look like and how the parallel lines look like. We can transfer the euclidean metric in the. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. Differential geometry is the study of (smooth) manifolds.
from notability.com
This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. We have explained there how the geodesics look like and how the parallel lines look like. We can transfer the euclidean metric in the. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. Descartes discovered that these types of geometries could be described by. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. The study concerns properties of sufficiently small pieces of them. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. Differential geometry is the study of (smooth) manifolds.
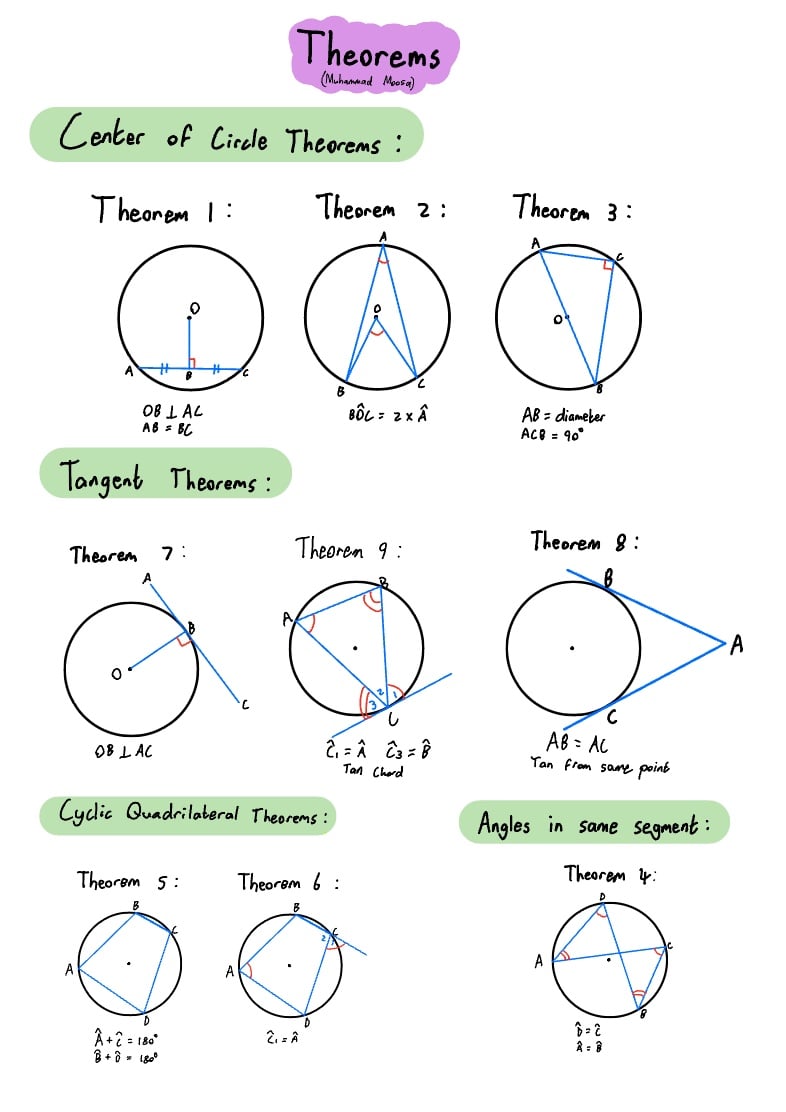
Euclidean Geometry Theorems Notability Gallery
Differential Geometry Vs Euclidean The study concerns properties of sufficiently small pieces of them. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. We can transfer the euclidean metric in the. The study concerns properties of sufficiently small pieces of them. Differential geometry is the study of (smooth) manifolds. We have explained there how the geodesics look like and how the parallel lines look like. Descartes discovered that these types of geometries could be described by. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures.
From www.youtube.com
"Introduction to Differential Geometry of Euclidean Space" (Lecture 5 Differential Geometry Vs Euclidean In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students.. Differential Geometry Vs Euclidean.
From www.pinterest.com
Comparison of Euclidean (planar), spherical, and hyperbolic geometry Differential Geometry Vs Euclidean Descartes discovered that these types of geometries could be described by. Differential geometry is the study of (smooth) manifolds. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn. Differential Geometry Vs Euclidean.
From www.youtube.com
What is the difference between Euclidean and Cartesian spaces? (2 Differential Geometry Vs Euclidean Descartes discovered that these types of geometries could be described by. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. Differential geometry is the study of (smooth) manifolds. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. We. Differential Geometry Vs Euclidean.
From www.pngwing.com
Abstract differential geometry Euclidean Circle, Commercial flat Differential Geometry Vs Euclidean We can transfer the euclidean metric in the. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. Differential geometry is the study of (smooth) manifolds. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. The study concerns properties of sufficiently small pieces of them. Descartes. Differential Geometry Vs Euclidean.
From www.youtube.com
Differential Geometry Lecture 9 part 1 Euclidean geometry of Rn YouTube Differential Geometry Vs Euclidean We have explained there how the geodesics look like and how the parallel lines look like. Differential geometry is the study of (smooth) manifolds. The study concerns properties of sufficiently small pieces of them. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. The former restricts attention to submanifolds of euclidean space. Differential Geometry Vs Euclidean.
From studylib.net
Chapter 4One Way to Go Euclidean Geometry of the Plane Differential Geometry Vs Euclidean This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. We can transfer the euclidean metric in the. Descartes discovered that these types of geometries could. Differential Geometry Vs Euclidean.
From www.teacharesources.com
Gr. 12 Euclidean Geometry Ratio & Proportionality • Teacha! Differential Geometry Vs Euclidean In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate. Differential Geometry Vs Euclidean.
From www.h-its.org
Comparing Hyperbolic and Euclidean Geometry HITS Differential Geometry Vs Euclidean In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. Descartes discovered that these types of geometries could be described by. This book is intented as a modern introduction. Differential Geometry Vs Euclidean.
From www.youtube.com
Euclidean Geometry (Proof of the The SSS Theorem) YouTube Differential Geometry Vs Euclidean This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. Descartes discovered that these types of geometries could be described by. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. Differential geometry is the study of (smooth) manifolds. We have explained there how the. Differential Geometry Vs Euclidean.
From blog.twitter.com
GNNs through the lens of differential geometry and algebraic topology Differential Geometry Vs Euclidean The study concerns properties of sufficiently small pieces of them. Differential geometry is the study of (smooth) manifolds. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. Descartes discovered that these types of geometries could be described by. We can transfer the euclidean metric in the. The former restricts attention to submanifolds. Differential Geometry Vs Euclidean.
From www.youtube.com
MATH335 SUNYGeneseo Neutral Geometry 13 Euclidean Parallel Postulate Differential Geometry Vs Euclidean The study concerns properties of sufficiently small pieces of them. Descartes discovered that these types of geometries could be described by. We can transfer the euclidean metric in the. Differential geometry is the study of (smooth) manifolds. We have explained there how the geodesics look like and how the parallel lines look like. In a plane, given a line and. Differential Geometry Vs Euclidean.
From www.geeksforgeeks.org
Geometry in Maths Definition, 2D & 3D Shapes, Formulas and Examples Differential Geometry Vs Euclidean The study concerns properties of sufficiently small pieces of them. We have explained there how the geodesics look like and how the parallel lines look like. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. Work in a euclidean space where we know how. Differential Geometry Vs Euclidean.
From mathoverflow.net
dg.differential geometry How to formally connect the logEuclidean Differential Geometry Vs Euclidean The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through.. Differential Geometry Vs Euclidean.
From studylib.net
Comparing Euclidean to Spherical Geometry Differential Geometry Vs Euclidean Differential geometry is the study of (smooth) manifolds. We have explained there how the geodesics look like and how the parallel lines look like. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes. Differential Geometry Vs Euclidean.
From www.slidemake.com
Euclid Geometry Presentation Differential Geometry Vs Euclidean In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. The study concerns properties of sufficiently small pieces of them. Descartes discovered that these types of geometries could be described by. We have explained there how the geodesics look like and how the parallel lines look like. Work in a euclidean space where. Differential Geometry Vs Euclidean.
From www.researchgate.net
Euclidean geometry x Fractal geometry. Download Scientific Diagram Differential Geometry Vs Euclidean In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. We can transfer the euclidean metric in the. The study concerns properties of sufficiently small pieces of them. We have explained there how the geodesics look like and how the parallel lines look like. Differential. Differential Geometry Vs Euclidean.
From www.wikihow.com
How to Understand Euclidean Geometry (with Pictures) Differential Geometry Vs Euclidean We can transfer the euclidean metric in the. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. We have explained there how the geodesics look like and how the parallel lines look like. Differential geometry is the study of (smooth) manifolds. The former restricts attention to submanifolds of. Differential Geometry Vs Euclidean.
From www.youtube.com
EUCLIDEAN GEOMETRY GRADE 10 REVISION ANGLES AND LINES YouTube Differential Geometry Vs Euclidean In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. We have explained there how the geodesics look like and how the parallel lines look like. The former. Differential Geometry Vs Euclidean.
From www.slidemake.com
Euclid Geometry Presentation Differential Geometry Vs Euclidean We have explained there how the geodesics look like and how the parallel lines look like. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. The former restricts attention. Differential Geometry Vs Euclidean.
From www.slideserve.com
PPT Euclidean Geometry PowerPoint Presentation, free download ID Differential Geometry Vs Euclidean We can transfer the euclidean metric in the. Differential geometry is the study of (smooth) manifolds. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students.. Differential Geometry Vs Euclidean.
From www.cuemath.com
Geometry Formulas, Examples Plane and Solid Geometry Differential Geometry Vs Euclidean Descartes discovered that these types of geometries could be described by. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. This book is. Differential Geometry Vs Euclidean.
From vccvisualization.org
Tutorial on Riemannian Geometry for Scientific Visualization (2022 Differential Geometry Vs Euclidean Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. Differential geometry is the study of (smooth) manifolds. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds. Differential Geometry Vs Euclidean.
From www.studocu.com
Grade 11 Euclidean Geometry Notes 19 Euclidean Geometry Parallel Differential Geometry Vs Euclidean The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. We can transfer the euclidean metric in the. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes. Differential Geometry Vs Euclidean.
From www.youtube.com
Strategy to approach euclidean geometry riders YouTube Differential Geometry Vs Euclidean We have explained there how the geodesics look like and how the parallel lines look like. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. Descartes discovered that these types of geometries could be described by. The study concerns properties of sufficiently small pieces of them. Differential geometry is the study of. Differential Geometry Vs Euclidean.
From www.youtube.com
Euclidean Geometry, all 7 Theorems YouTube Differential Geometry Vs Euclidean In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. We have explained there how the geodesics look like and how the parallel lines look like.. Differential Geometry Vs Euclidean.
From notability.com
Euclidean Geometry Theorems Notability Gallery Differential Geometry Vs Euclidean This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. We can transfer the euclidean metric in the. The study concerns properties of sufficiently small pieces of them. Descartes discovered that these types of geometries could be described by. Work in a euclidean space where we know how to compute distances,. Differential Geometry Vs Euclidean.
From ioqm.in
Euclidean Geometry Unlocking the Beauty of Geometric Principles Differential Geometry Vs Euclidean We have explained there how the geodesics look like and how the parallel lines look like. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. In a plane, given a line and a point not on it, at most one line parallel to the given line can be. Differential Geometry Vs Euclidean.
From www.taylorfrancis.com
Curves and Surfaces in ndimensional Euclidean Space Taylor & Francis Differential Geometry Vs Euclidean Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. Differential geometry is the study of (smooth) manifolds. In differential geometry the properties of curves and surfaces are usually studied. Differential Geometry Vs Euclidean.
From www.science.org
Supertwisted spirals of layered materials enabled by growth on non Differential Geometry Vs Euclidean Differential geometry is the study of (smooth) manifolds. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. Descartes discovered that these types of geometries could be described by.. Differential Geometry Vs Euclidean.
From www.youtube.com
1.1 Differential Geometry Euclidean Space YouTube Differential Geometry Vs Euclidean Descartes discovered that these types of geometries could be described by. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. We can transfer the euclidean metric in the. We. Differential Geometry Vs Euclidean.
From www.scribd.com
3.the Euclidean E 2 PDF Differential Geometry Geometry Differential Geometry Vs Euclidean The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. We have explained there how the geodesics look like and how the parallel lines look like. Descartes discovered that these types of geometries could be described by. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes. Differential Geometry Vs Euclidean.
From math.stackexchange.com
differential geometry How is dx^2+dy^2 the Euclidean metric on Differential Geometry Vs Euclidean We have explained there how the geodesics look like and how the parallel lines look like. The study concerns properties of sufficiently small pieces of them. Descartes discovered that these types of geometries could be described by. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced undergraduate students. Work in a euclidean. Differential Geometry Vs Euclidean.
From www.slideserve.com
PPT Basics of Euclidean Geometry PowerPoint Presentation, free Differential Geometry Vs Euclidean Differential geometry is the study of (smooth) manifolds. The study concerns properties of sufficiently small pieces of them. Descartes discovered that these types of geometries could be described by. We can transfer the euclidean metric in the. The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. In differential geometry the properties of curves. Differential Geometry Vs Euclidean.
From www.youtube.com
Euclidean geometry Theorem 9 YouTube Differential Geometry Vs Euclidean The former restricts attention to submanifolds of euclidean space while the latter studies manifolds equipped with. Work in a euclidean space where we know how to compute distances, angles, areas, and even volumes of simple geometric figures. We can transfer the euclidean metric in the. In differential geometry the properties of curves and surfaces are usually studied on a small. Differential Geometry Vs Euclidean.
From www.youtube.com
Midpoint theorem and converse Euclidean explained Grade 10+12 (mathdou Differential Geometry Vs Euclidean In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through. Differential geometry is the study of (smooth) manifolds. The study concerns properties of sufficiently small pieces of them. This book is intented as a modern introduction to differential geometry, at a level accessible to advanced. Differential Geometry Vs Euclidean.