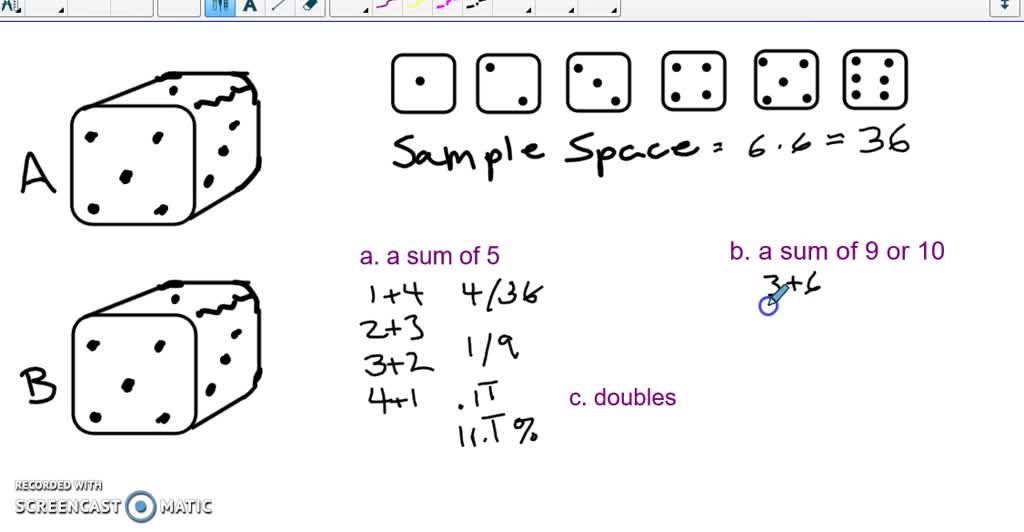
When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet . Find the probability that the numbers on the two dices are different? That is, x = {1,2,3,4,5,6} and y = {1,2,3,4,5,6}. (1,1), (2,2), (3,3), (4,4), (5,5), (6,6). For two dice, you should multiply. Getting a double six (6, 6) at least once in the total of $n$ throws of. Find the probability of getting: Two dice, one blue and one orange, are rolled simultaneously. (b) a doublet of even numbers. The total number of outcomes of the two dices is 36. Basically, we like to find the probability of the event $a$: Two dice are thrown simultaneously. C) getting sum ≤ 4. The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), Find the probability of getting a doublet. When the two dice are thrown simultaneously, all possible outcomes = 6 2 = 36.
from www.numerade.com
Two dice are thrown simultaneously. (1,1), (2,2), (3,3), (4,4), (5,5), (6,6). There are 36 outcomes when you throw two dice. Basically, we like to find the probability of the event $a$: Two dice are rolled at a time. (a) the sum as a prime number. For a single die, there are six faces, and for any roll, there are six possible outcomes. Two dice are thrown simultaneously. We roll two dice simultaneously, what is the probability of the following events: C) getting sum ≤ 4.
SOLVEDTwo dice are thrown simultaneously. Find the probability of
When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet The total number of outcomes of the two dices is 36. The total number of outcomes of the two dices is 36. Two dice, one blue and one orange, are rolled simultaneously. There are 36 outcomes when you throw two dice. Find the probability of getting: We roll two dice simultaneously, what is the probability of the following events: C) getting sum ≤ 4. When the two dice are thrown simultaneously, all possible outcomes = 6 2 = 36. Let us look at the sample when two dice are rolled. (1,1), (2,2), (3,3), (4,4), (5,5), (6,6). Two dice are rolled at a time. (b) a doublet of even numbers. That is, x = {1,2,3,4,5,6} and y = {1,2,3,4,5,6}. (a) the sum as a prime number. Find the probability of getting (i) equal numbers on both (ii) two numbers appearing on them whose sum is 9. Two dice are thrown simultaneously.
From byjus.com
62. if two dice are thrown simultaneously, then the probability of When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet A) getting sum divisible by 6. (a) the sum as a prime number. For a single die, there are six faces, and for any roll, there are six possible outcomes. Two dice, one blue and one orange, are rolled simultaneously. Two dice are thrown simultaneously. For two dice, you should multiply. Two dice are rolled at a time. Two dice. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
If two dice are thrown simultaneously, then the probability of getting When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet C) getting sum ≤ 4. Two dice are rolled at a time. For two dice, you should multiply. Let us look at the sample when two dice are rolled. (a) the sum as a prime number. Basically, we like to find the probability of the event $a$: Find the probability that the numbers on the two dices are different? (1,1),. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
Two dice are thrown simultaneously, then what is the probability that 5 When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Two dice are rolled at a time. B) getting a total of at least 9. When the two dice are thrown simultaneously, all possible outcomes = 6 2 = 36. The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1),. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.teachoo.com
Question 11 Two dice are thrown. If X is number of sixes When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet (b) a doublet of even numbers. For a single die, there are six faces, and for any roll, there are six possible outcomes. Two dice are thrown simultaneously. Let us look at the sample when two dice are rolled. C) getting sum ≤ 4. (a) the sum as a prime number. Find the probability of getting a doublet. Two dice. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
Two dice are thrown simultaneously. What is the probability that the When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Getting a double six (6, 6) at least once in the total of $n$ throws of. Basically, we like to find the probability of the event $a$: Find the probability of getting a doublet. The total number of outcomes of the two dices is 36. B) getting a total of at least 9. C) getting sum ≤ 4. Find the. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.doubtnut.com
Two dice are thrown simultaneously. Find the probability of getting When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet There are 36 outcomes when you throw two dice. B) getting a total of at least 9. Find the probability of getting a doublet. Basically, we like to find the probability of the event $a$: (1,1), (2,2), (3,3), (4,4), (5,5), (6,6). Two dice are thrown simultaneously. Two dice are rolled at a time. The possible outcomes are (1, 1), (1,. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.meritnation.com
Two dice are thrown simultaneously what is the probability that 1)5 When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Find the probability of getting: We roll two dice simultaneously, what is the probability of the following events: Let us look at the sample when two dice are rolled. Two dice are rolled at a time. When the two dice are thrown simultaneously, all possible outcomes = 6 2 = 36. Find the probability of getting a doublet. Two dice,. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From brainly.in
Two dice are thrown together.Find the probability of getting the same When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Find the probability of getting a doublet. Let us look at the sample when two dice are rolled. Two dice are thrown simultaneously. Basically, we like to find the probability of the event $a$: For a single die, there are six faces, and for any roll, there are six possible outcomes. (a) the sum as a prime number. For two. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.doubtnut.com
Two dice are thrown simultaneously. Find the probability of getting an When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Find the probability of getting (i) equal numbers on both (ii) two numbers appearing on them whose sum is 9. Find the probability of getting a doublet. C) getting sum ≤ 4. (b) a doublet of even numbers. The total number of outcomes of the two dices is 36. Two dice, one blue and one orange, are rolled simultaneously. Two. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.youtube.com
Two dice are thrown simultaneously find probability of getting a When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Two dice are rolled at a time. (a) the sum as a prime number. Find the probability of getting: A) getting sum divisible by 6. The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3,. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From askfilo.com
10. Two dice are thrown simultaneously find the probability that the sum When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet For two dice, you should multiply. There are 36 outcomes when you throw two dice. The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), When the two dice are. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
Two dice are thrown simultaneously. What is the probability that the When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), We roll two dice simultaneously, what is the probability of the following events: For two dice, you should multiply. B). When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From byjus.com
15. Two dice are thrown simultaneously, find the probability of (i) 3 When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (a) the sum as a prime number. For a single die, there are six faces, and for any roll, there. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
a) Two different dice are thrown the same time. Find the probability of When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet The total number of outcomes of the two dices is 36. Two dice are rolled at a time. Find the probability that the numbers on the two dices are different? Two dice are thrown simultaneously. Basically, we like to find the probability of the event $a$: Find the probability of getting: That is, x = {1,2,3,4,5,6} and y = {1,2,3,4,5,6}.. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From alumnos.planeaciondidactica.cucea.udg.mx
Two dice are thrown simultaneously. Find the probability of getting When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet When the two dice are thrown simultaneously, all possible outcomes = 6 2 = 36. The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), Basically, we like to find. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.youtube.com
Two dice are rolled simultaneously. Find the probability of getting a When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet We roll two dice simultaneously, what is the probability of the following events: C) getting sum ≤ 4. For a single die, there are six faces, and for any roll, there are six possible outcomes. (1,1), (2,2), (3,3), (4,4), (5,5), (6,6). The total number of outcomes of the two dices is 36. The possible outcomes are (1, 1), (1, 2),. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.teachoo.com
Two dice are thrown at the same time and the product of numbers appear When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet B) getting a total of at least 9. Find the probability that the numbers on the two dices are different? There are 36 outcomes when you throw two dice. When the two dice are thrown simultaneously, all possible outcomes = 6 2 = 36. Two dice are thrown simultaneously. Find the probability of getting: Let us look at the sample. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.youtube.com
Two dice are thrown simultaneously. Find the probability that the When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet (1,1), (2,2), (3,3), (4,4), (5,5), (6,6). Basically, we like to find the probability of the event $a$: We roll two dice simultaneously, what is the probability of the following events: For a single die, there are six faces, and for any roll, there are six possible outcomes. For two dice, you should multiply. C) getting sum ≤ 4. Let us. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.teachoo.com
Question 2 A pair of dice is thrown 4 times. Getting doublet When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Basically, we like to find the probability of the event $a$: The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), Two dice are rolled at a time. The total. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.chegg.com
Solved Two dice are thrown simultaneously. Find the When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet For a single die, there are six faces, and for any roll, there are six possible outcomes. Getting a double six (6, 6) at least once in the total of $n$ throws of. A) getting sum divisible by 6. Find the probability that the numbers on the two dices are different? We roll two dice simultaneously, what is the probability. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
Two dice are thrown simultaneously. Find the probability of gettinga When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet A) getting sum divisible by 6. That is, x = {1,2,3,4,5,6} and y = {1,2,3,4,5,6}. Getting a double six (6, 6) at least once in the total of $n$ throws of. B) getting a total of at least 9. Find the probability of getting a doublet. Two dice, one blue and one orange, are rolled simultaneously. Two dice are thrown. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
Two dice are thrown simultaneously. The probability of getting a When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet (b) a doublet of even numbers. B) getting a total of at least 9. A) getting sum divisible by 6. Two dice are thrown simultaneously. Find the probability of getting (i) equal numbers on both (ii) two numbers appearing on them whose sum is 9. Find the probability of getting: Let us look at the sample when two dice are. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
4. Two dice are thrown simultaneously. Find the probability of getting When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Let us look at the sample when two dice are rolled. For a single die, there are six faces, and for any roll, there are six possible outcomes. Basically, we like to find the probability of the event $a$: For two dice, you should multiply. Find the probability of getting a doublet. A) getting sum divisible by 6. We roll. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.numerade.com
SOLVEDTwo dice are thrown simultaneously. Find the probability of When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet B) getting a total of at least 9. Basically, we like to find the probability of the event $a$: Two dice are thrown simultaneously. Find the probability of getting: (a) the sum as a prime number. We roll two dice simultaneously, what is the probability of the following events: Two dice are rolled at a time. Find the probability of. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From quantitative-probabilitydistribution.blogspot.com
Probability Distribution Table 2 Dice Research Topics When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet (1,1), (2,2), (3,3), (4,4), (5,5), (6,6). The total number of outcomes of the two dices is 36. The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (b) a doublet. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.omtexclasses.com
OMTEX CLASSES Two unbiased dice are rolled once. Find the probability When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), Two dice, one blue and one orange, are rolled simultaneously. Let us look at the sample when two dice are. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.teachoo.com
Find the probability of getting a doublet in a throw of a pair of dice When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet There are 36 outcomes when you throw two dice. Find the probability of getting: Basically, we like to find the probability of the event $a$: Find the probability of getting a doublet. Find the probability of getting (i) equal numbers on both (ii) two numbers appearing on them whose sum is 9. The total number of outcomes of the two. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
Two dice are thrown simultaneously. Find the probability of gettinga When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet (a) the sum as a prime number. The total number of outcomes of the two dices is 36. Find the probability that the numbers on the two dices are different? For two dice, you should multiply. Let us look at the sample when two dice are rolled. Find the probability of getting a doublet. We roll two dice simultaneously, what. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.youtube.com
two dice are thrown simultaneously find the probability of getting a When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Find the probability that the numbers on the two dices are different? The total number of outcomes of the two dices is 36. Let us look at the sample when two dice are rolled. There are 36 outcomes when you throw two dice. When the two dice are thrown simultaneously, all possible outcomes = 6 2 = 36. For a. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.teachoo.com
[MCQ] Two dice are rolled simultaneously. What is the probability When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Getting a double six (6, 6) at least once in the total of $n$ throws of. (b) a doublet of even numbers. There are 36 outcomes when you throw two dice. Let us look at the sample when two dice are rolled. (1,1), (2,2), (3,3), (4,4), (5,5), (6,6). C) getting sum ≤ 4. Two dice are thrown simultaneously. Find the. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From byjus.com
27. Two different dice are thrown together. Find the probability that When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet C) getting sum ≤ 4. Let us look at the sample when two dice are rolled. For two dice, you should multiply. Two dice are thrown simultaneously. The total number of outcomes of the two dices is 36. The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3),. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.teachoo.com
Ques 27 (MCQ) Two fair dice are rolled simultaneously. Probability When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet That is, x = {1,2,3,4,5,6} and y = {1,2,3,4,5,6}. B) getting a total of at least 9. Two dice are thrown simultaneously. Find the probability of getting: Two dice are thrown simultaneously. The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.teachoo.com
Example 13 Two dice, one blue and one grey are thrown Examples When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Find the probability that the numbers on the two dices are different? Two dice, one blue and one orange, are rolled simultaneously. Find the probability of getting: The total number of outcomes of the two dices is 36. For a single die, there are six faces, and for any roll, there are six possible outcomes. There are 36 outcomes when. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.toppr.com
Two dice are thrown simultaneously. The probability of getting a When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet (1,1), (2,2), (3,3), (4,4), (5,5), (6,6). That is, x = {1,2,3,4,5,6} and y = {1,2,3,4,5,6}. Two dice, one blue and one orange, are rolled simultaneously. (a) the sum as a prime number. There are 36 outcomes when you throw two dice. The possible outcomes are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2,. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.
From www.teachoo.com
MCQ Class 10 2 dice are thrown together. The Probability of getting When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet Two dice are rolled at a time. There are 36 outcomes when you throw two dice. (a) the sum as a prime number. B) getting a total of at least 9. C) getting sum ≤ 4. Basically, we like to find the probability of the event $a$: Find the probability of getting: Two dice are thrown simultaneously. Find the probability. When Two Dice Are Thrown Simultaneously Find The Probability Of Getting A Doublet.