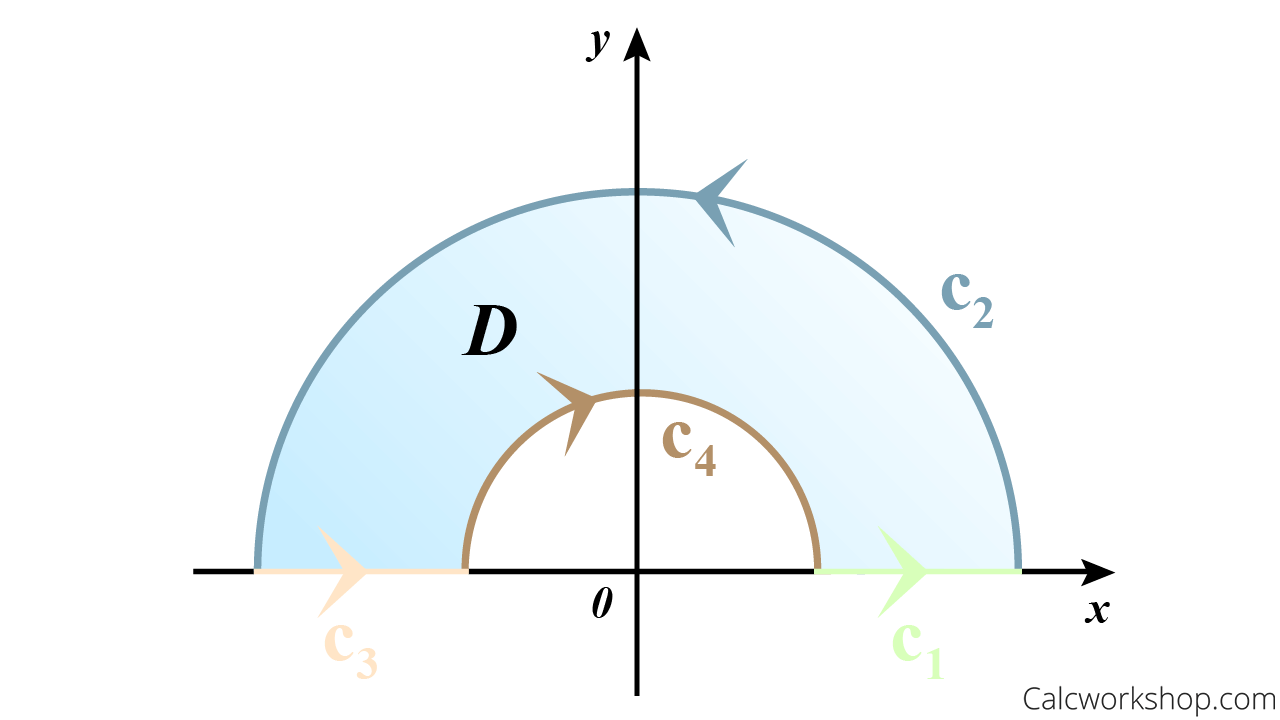
Green's Theorem Examples . Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. It is related to many theorems such as gauss theorem, stokes theorem. Other ways of writing green's theorem; See examples of simple and multiply connected regions, and. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. This theorem shows the relationship between a line integral and a surface integral. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is mainly used for the integration of the line combined with a curved plane. This theorem helps us understand how line and. The idea behind green's theorem; Green’s theorem is used to integrate the derivatives in a particular plane. Using green's theorem to find area;.
from calcworkshop.com
This theorem shows the relationship between a line integral and a surface integral. This theorem helps us understand how line and. Using green's theorem to find area;. Other ways of writing green's theorem; It is related to many theorems such as gauss theorem, stokes theorem. Green’s theorem is mainly used for the integration of the line combined with a curved plane. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is used to integrate the derivatives in a particular plane. The idea behind green's theorem; If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized.
Green's Theorem (Fully Explained w/ StepbyStep Examples!)
Green's Theorem Examples This theorem helps us understand how line and. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. Green’s theorem is used to integrate the derivatives in a particular plane. Green’s theorem is mainly used for the integration of the line combined with a curved plane. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. This theorem shows the relationship between a line integral and a surface integral. Using green's theorem to find area;. This theorem helps us understand how line and. It is related to many theorems such as gauss theorem, stokes theorem. See examples of simple and multiply connected regions, and. Other ways of writing green's theorem; The idea behind green's theorem;
From answerkeyformath.com
Green's Theorem Examples And Solutions Answer Key for Math Green's Theorem Examples This theorem helps us understand how line and. See examples of simple and multiply connected regions, and. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. This theorem shows. Green's Theorem Examples.
From www.youtube.com
Green's theorem example 1 Multivariable Calculus Khan Academy YouTube Green's Theorem Examples See examples of simple and multiply connected regions, and. It is related to many theorems such as gauss theorem, stokes theorem. Green’s theorem is used to integrate the derivatives in a particular plane. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. This theorem shows the relationship. Green's Theorem Examples.
From www.numerade.com
Green's theorem example 3 Numerade Green's Theorem Examples Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is used to integrate the derivatives in a particular plane. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which. Green's Theorem Examples.
From www.youtube.com
How to Use Green's Theorem Example with Integral((y x)dx + (2x y Green's Theorem Examples Using green's theorem to find area;. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. This theorem shows the relationship between a line integral and a surface integral. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. See examples of simple and multiply connected regions,. Green's Theorem Examples.
From www.youtube.com
Multivariable Calculus Green's Theorem YouTube Green's Theorem Examples The idea behind green's theorem; See examples of simple and multiply connected regions, and. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is used to integrate the derivatives in a particular plane. Green’s theorem is mainly used for the integration of the line combined with a curved plane.. Green's Theorem Examples.
From www.beautifulequation.com
Beautiful Equations Explained… Green’s Theorem Green's Theorem Examples Green’s theorem is used to integrate the derivatives in a particular plane. Green’s theorem is mainly used for the integration of the line combined with a curved plane. The idea behind green's theorem; See examples of simple and multiply connected regions, and. This theorem shows the relationship between a line integral and a surface integral. If f~(x;y) = [p(x;y);q(x;y)]t is. Green's Theorem Examples.
From www.youtube.com
Green's Theorem Video 1 YouTube Green's Theorem Examples This theorem shows the relationship between a line integral and a surface integral. See examples of simple and multiply connected regions, and. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. Green’s theorem is used to integrate the derivatives in a particular plane. Green’s theorem is mainly used for the integration of the line. Green's Theorem Examples.
From www.youtube.com
Green's Theorem Visualization and Examples on Mathematica YouTube Green's Theorem Examples Using green's theorem to find area;. The idea behind green's theorem; This theorem shows the relationship between a line integral and a surface integral. Green’s theorem is used to integrate the derivatives in a particular plane. See examples of simple and multiply connected regions, and. Other ways of writing green's theorem; If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and. Green's Theorem Examples.
From www.youtube.com
Green's Theorem Example 1 YouTube Green's Theorem Examples Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. It is related to many theorems such as gauss theorem, stokes theorem. See examples of simple and multiply connected regions, and. Green’s theorem. Green's Theorem Examples.
From www.youtube.com
Green's Theorem Example Calculus 3 Vector Calculus YouTube Green's Theorem Examples Other ways of writing green's theorem; If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. The idea behind green's theorem; Green’s theorem is mainly used for the integration of. Green's Theorem Examples.
From www.youtube.com
Example Green's Theorem (1) YouTube Green's Theorem Examples Green’s theorem is used to integrate the derivatives in a particular plane. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. It is related to many theorems such as gauss theorem, stokes theorem. Using green's theorem to find area;. This theorem shows the relationship between a line integral and a surface. Green's Theorem Examples.
From www.youtube.com
2D Green's Theorem Example Solving Both Sides of the Equation YouTube Green's Theorem Examples This theorem shows the relationship between a line integral and a surface integral. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. See examples of simple and multiply connected regions, and. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is mainly used. Green's Theorem Examples.
From answerkeyformath.com
Green's Theorem Examples And Solutions Answer Key for Math Green's Theorem Examples See examples of simple and multiply connected regions, and. Other ways of writing green's theorem; If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. The idea behind green's theorem; Using green's theorem. Green's Theorem Examples.
From www.studypool.com
SOLUTION Green's Theorem in Vector Calculus Studypool Green's Theorem Examples The idea behind green's theorem; Other ways of writing green's theorem; This theorem shows the relationship between a line integral and a surface integral. See examples of simple and multiply connected regions, and. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. Green’s theorem is mainly used. Green's Theorem Examples.
From www.worksheetsplanet.com
The Green's Theorem Formula + Definition Green's Theorem Examples Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is used to integrate the derivatives in a particular plane. This theorem shows the relationship between a line integral and a surface integral. It is. Green's Theorem Examples.
From www.youtube.com
Green's Theorem, explained visually YouTube Green's Theorem Examples This theorem helps us understand how line and. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. Green’s theorem is used to integrate the derivatives in a particular plane. See examples of simple and multiply connected. Green's Theorem Examples.
From byjus.com
Green’s Theorem (Statement & Proof) Formula and Example Green's Theorem Examples Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. This theorem helps us understand how line and. Green’s theorem is used to integrate the derivatives in a particular plane. It is related to many theorems such as gauss theorem, stokes theorem. This theorem shows the relationship between a line integral and a surface integral.. Green's Theorem Examples.
From answerkeyformath.com
Green's Theorem Examples And Solutions Answer Key for Math Green's Theorem Examples Green’s theorem is used to integrate the derivatives in a particular plane. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. The idea behind green's theorem; It is related to many theorems such as gauss theorem, stokes theorem. See examples of simple and multiply connected regions, and.. Green's Theorem Examples.
From www.wikihow.com
How to Use Green's Theorem 4 Steps wikiHow Green's Theorem Examples It is related to many theorems such as gauss theorem, stokes theorem. Using green's theorem to find area;. This theorem shows the relationship between a line integral and a surface integral. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for. Green's Theorem Examples.
From www.youtube.com
Green's theorem examples and solution YouTube Green's Theorem Examples See examples of simple and multiply connected regions, and. Other ways of writing green's theorem; This theorem shows the relationship between a line integral and a surface integral. It is related to many theorems such as gauss theorem, stokes theorem. Green’s theorem is used to integrate the derivatives in a particular plane. The idea behind green's theorem; Green’s theorem is. Green's Theorem Examples.
From calcworkshop.com
Green's Theorem (Fully Explained w/ StepbyStep Examples!) Green's Theorem Examples The idea behind green's theorem; Green’s theorem is mainly used for the integration of the line combined with a curved plane. This theorem helps us understand how line and. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. Green’s theorem is used to integrate the derivatives in a particular plane. It is related to. Green's Theorem Examples.
From www.youtube.com
Green's theorem examples and solution YouTube Green's Theorem Examples The idea behind green's theorem; Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. This theorem shows the relationship between a line integral and a surface integral. It is related to many theorems such as gauss theorem, stokes theorem. Green’s theorem is used to integrate the derivatives in a particular plane.. Green's Theorem Examples.
From www.youtube.com
Green's Theorem Part 2 YouTube Green's Theorem Examples Other ways of writing green's theorem; Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. The idea behind green's theorem; If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. See examples of simple and multiply connected regions, and. Learn how to. Green's Theorem Examples.
From www.youtube.com
Green's Theorem YouTube Green's Theorem Examples This theorem shows the relationship between a line integral and a surface integral. Other ways of writing green's theorem; See examples of simple and multiply connected regions, and. Green’s theorem is mainly used for the integration of the line combined with a curved plane. It is related to many theorems such as gauss theorem, stokes theorem. Green’s theorem is one. Green's Theorem Examples.
From www.youtube.com
Green's Theorem Part 2/3 "Green's Theorem" YouTube Green's Theorem Examples Green’s theorem is used to integrate the derivatives in a particular plane. Green’s theorem is mainly used for the integration of the line combined with a curved plane. The idea behind green's theorem; Using green's theorem to find area;. This theorem shows the relationship between a line integral and a surface integral. Other ways of writing green's theorem; Learn how. Green's Theorem Examples.
From www.geneseo.edu
Geneseo Math 223 Green’s Theorem Examples 2 Green's Theorem Examples This theorem helps us understand how line and. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. Other ways of writing green's theorem; Green’s theorem is used to integrate the derivatives in a particular plane. Green’s theorem is mainly used for the integration of the line combined with a curved plane. The idea behind. Green's Theorem Examples.
From youtube.com
Green's Theorem Part 1 YouTube Green's Theorem Examples The idea behind green's theorem; Using green's theorem to find area;. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. It is related to many theorems such as gauss theorem, stokes theorem. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is used. Green's Theorem Examples.
From www.scribd.com
Green's Theorem Examples PDF Integral Linear Algebra Green's Theorem Examples It is related to many theorems such as gauss theorem, stokes theorem. This theorem shows the relationship between a line integral and a surface integral. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region for which the boundary c is a curve parametrized. Green’s theorem is used to integrate the derivatives in a particular plane. Other. Green's Theorem Examples.
From www.youtube.com
Applications of Green's Theorem/Problem2 on Green's Theorem in Green's Theorem Examples Other ways of writing green's theorem; It is related to many theorems such as gauss theorem, stokes theorem. The idea behind green's theorem; This theorem helps us understand how line and. Green’s theorem is mainly used for the integration of the line combined with a curved plane. If f~(x;y) = [p(x;y);q(x;y)]t is a vector eld and g is a region. Green's Theorem Examples.
From www.geneseo.edu
Geneseo Math 223 Green’s Theorem Examples Green's Theorem Examples The idea behind green's theorem; Using green's theorem to find area;. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is used to integrate the derivatives in a particular plane. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. If f~(x;y) = [p(x;y);q(x;y)]t. Green's Theorem Examples.
From www.youtube.com
12]Green’s Theorem with Examples Vector Analysis Engineering Green's Theorem Examples Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. Green’s theorem is used to integrate the derivatives in a particular plane. Other ways of writing green's theorem; The idea behind green's theorem; Using green's theorem to find area;. Green’s theorem is one of the most important theorems that you’ll learn in. Green's Theorem Examples.
From www.youtube.com
Green's Theorem 1 Vector Calculus YouTube Green's Theorem Examples This theorem shows the relationship between a line integral and a surface integral. See examples of simple and multiply connected regions, and. Green’s theorem is mainly used for the integration of the line combined with a curved plane. Green’s theorem is one of the most important theorems that you’ll learn in vector calculus. The idea behind green's theorem; Other ways. Green's Theorem Examples.
From www.youtube.com
Multivariable calculus 4.3.3 Examples of Green's theorem YouTube Green's Theorem Examples Using green's theorem to find area;. It is related to many theorems such as gauss theorem, stokes theorem. This theorem shows the relationship between a line integral and a surface integral. This theorem helps us understand how line and. See examples of simple and multiply connected regions, and. Green’s theorem is mainly used for the integration of the line combined. Green's Theorem Examples.
From calcworkshop.com
Green's Theorem (Fully Explained w/ StepbyStep Examples!) Green's Theorem Examples Using green's theorem to find area;. Learn how to apply green's theorem to convert line integrals on closed curves to double integrals over regions. This theorem shows the relationship between a line integral and a surface integral. Green’s theorem is used to integrate the derivatives in a particular plane. It is related to many theorems such as gauss theorem, stokes. Green's Theorem Examples.
From www.numerade.com
Green's theorem example 3 Numerade Green's Theorem Examples The idea behind green's theorem; It is related to many theorems such as gauss theorem, stokes theorem. Green’s theorem is mainly used for the integration of the line combined with a curved plane. Other ways of writing green's theorem; Using green's theorem to find area;. This theorem helps us understand how line and. Green’s theorem is one of the most. Green's Theorem Examples.