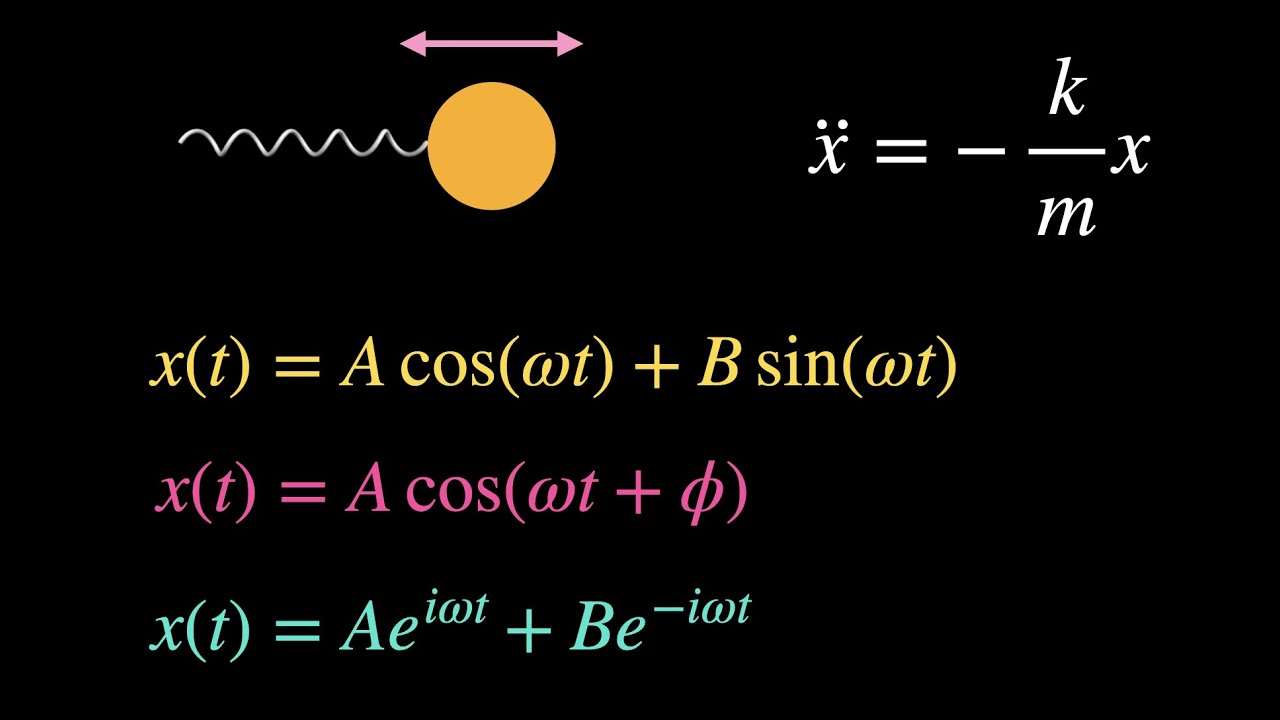Harmonic Oscillator Differential Equation . Simple harmonic oscillator equation (sho). Explore the kinematics and dynamics of mass. Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Find the solution in terms. Because the spring force depends on the. The harmonic oscillator, which we are about to study, has close analogs in many other fields; Where k is the spring constant and m is the mass of the oscillating body that is attached to the. This equation of motion, eq. We wish to solve the equation of motion for the simple harmonic oscillator: How to solve harmonic oscillator differential equation: Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Although we start with a mechanical example of.
from www.youtube.com
Although we start with a mechanical example of. Where k is the spring constant and m is the mass of the oscillating body that is attached to the. How to solve harmonic oscillator differential equation: Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. Find the solution in terms. Because the spring force depends on the. We wish to solve the equation of motion for the simple harmonic oscillator: Simple harmonic oscillator equation (sho). The harmonic oscillator, which we are about to study, has close analogs in many other fields; Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion.
Three Solutions for a Simple Harmonic Oscillator (with initial
Harmonic Oscillator Differential Equation Where k is the spring constant and m is the mass of the oscillating body that is attached to the. Where k is the spring constant and m is the mass of the oscillating body that is attached to the. Although we start with a mechanical example of. How to solve harmonic oscillator differential equation: Explore the kinematics and dynamics of mass. This equation of motion, eq. Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Simple harmonic oscillator equation (sho). Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Because the spring force depends on the. Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ The harmonic oscillator, which we are about to study, has close analogs in many other fields; We wish to solve the equation of motion for the simple harmonic oscillator: Find the solution in terms.
From www.youtube.com
simple harmonic oscillator differential equation and solution imran Harmonic Oscillator Differential Equation The harmonic oscillator, which we are about to study, has close analogs in many other fields; Simple harmonic oscillator equation (sho). How to solve harmonic oscillator differential equation: Although we start with a mechanical example of. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ This equation of motion, eq. We wish to solve the equation of motion for the simple harmonic oscillator: Dividing. Harmonic Oscillator Differential Equation.
From www.youtube.com
Differential Equation of Damped Harmonic Oscillator YouTube Harmonic Oscillator Differential Equation Explore the kinematics and dynamics of mass. This equation of motion, eq. Simple harmonic oscillator equation (sho). $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Although we start with a mechanical example of. The harmonic oscillator, which we are about. Harmonic Oscillator Differential Equation.
From www.houseofmath.com
The Differential Equation for Harmonic Oscillators Harmonic Oscillator Differential Equation Where k is the spring constant and m is the mass of the oscillating body that is attached to the. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Although we start with a mechanical example of. This equation of motion, eq. Simple harmonic oscillator equation (sho). Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's. Harmonic Oscillator Differential Equation.
From slidetodoc.com
Mechanical Energy and Simple Harmonic Oscillator 8 01 Harmonic Oscillator Differential Equation $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Find the solution in terms. How to solve harmonic oscillator differential equation: Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. Where k is the spring constant and m is the mass of the oscillating body that is attached to the. We wish to solve the. Harmonic Oscillator Differential Equation.
From www.numerade.com
SOLVED Solve the differential equation of motion of the damped Harmonic Oscillator Differential Equation Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. Simple harmonic oscillator equation (sho). Although we start with a mechanical example of. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ We. Harmonic Oscillator Differential Equation.
From www.youtube.com
QMSHOL2 Solution to Simple Harmonic Oscillator differential Harmonic Oscillator Differential Equation The harmonic oscillator, which we are about to study, has close analogs in many other fields; Simple harmonic oscillator equation (sho). Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Explore the kinematics and dynamics of mass. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ How to solve harmonic oscillator differential equation: Although we start with. Harmonic Oscillator Differential Equation.
From studylib.net
The Damped Harmonic Oscillator Consider the differential equation y Harmonic Oscillator Differential Equation Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Because the spring force depends on the. Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. Explore the kinematics and dynamics of mass. Find the solution in terms. Dividing by the mass, this equation can. Harmonic Oscillator Differential Equation.
From www.slideserve.com
PPT The Harmonic Oscillator PowerPoint Presentation, free download Harmonic Oscillator Differential Equation Although we start with a mechanical example of. We wish to solve the equation of motion for the simple harmonic oscillator: Explore the kinematics and dynamics of mass. Simple harmonic oscillator equation (sho). This equation of motion, eq. Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Dividing by the mass, this equation. Harmonic Oscillator Differential Equation.
From owlcation.com
Solution of Schrödinger Equation for Simple Harmonic Oscillator Owlcation Harmonic Oscillator Differential Equation Because the spring force depends on the. Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. Although we start with a mechanical example of. Where k is the spring constant and m is the mass of the oscillating body that is attached to the. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ We wish. Harmonic Oscillator Differential Equation.
From www.youtube.com
simple harmonic motion solving the simple harmonic oscillator Harmonic Oscillator Differential Equation We wish to solve the equation of motion for the simple harmonic oscillator: The harmonic oscillator, which we are about to study, has close analogs in many other fields; How to solve harmonic oscillator differential equation: Because the spring force depends on the. This equation of motion, eq. Explore the kinematics and dynamics of mass. Dividing by the mass, this. Harmonic Oscillator Differential Equation.
From www.houseofmath.com
The Differential Equation for Harmonic Oscillators Harmonic Oscillator Differential Equation Because the spring force depends on the. We wish to solve the equation of motion for the simple harmonic oscillator: How to solve harmonic oscillator differential equation: Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Dividing by the mass, this equation can be written in the form. Harmonic Oscillator Differential Equation.
From www.youtube.com
Damped Harmonic Oscillator (Differential Equation and Solution of Harmonic Oscillator Differential Equation Explore the kinematics and dynamics of mass. We wish to solve the equation of motion for the simple harmonic oscillator: Simple harmonic oscillator equation (sho). Because the spring force depends on the. Where k is the spring constant and m is the mass of the oscillating body that is attached to the. Learn how to derive the differential equation for. Harmonic Oscillator Differential Equation.
From www.chegg.com
Solved A simple harmonic oscillator obeys the differential Harmonic Oscillator Differential Equation Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Because the spring force depends on the. This equation of motion, eq. Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Where k is the. Harmonic Oscillator Differential Equation.
From www.youtube.com
Harmonic oscillator Differential equation YouTube Harmonic Oscillator Differential Equation $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Explore the kinematics and dynamics of mass. How to solve harmonic oscillator differential equation: Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Where k is the spring constant and m is the mass of the oscillating body that is attached. Harmonic Oscillator Differential Equation.
From poretkings.weebly.com
Harmonic oscillator equation poretkings Harmonic Oscillator Differential Equation Because the spring force depends on the. Where k is the spring constant and m is the mass of the oscillating body that is attached to the. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Explore the kinematics and dynamics of mass. Find the solution in terms. Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion.. Harmonic Oscillator Differential Equation.
From www.youtube.com
SecondOrder Ordinary Differential Equations Solving the Harmonic Harmonic Oscillator Differential Equation We wish to solve the equation of motion for the simple harmonic oscillator: Find the solution in terms. Where k is the spring constant and m is the mass of the oscillating body that is attached to the. The harmonic oscillator, which we are about to study, has close analogs in many other fields; Learn how to derive the differential. Harmonic Oscillator Differential Equation.
From www.youtube.com
Dynamics Lecture Simple Harmonic Oscillator,MassSpring, Natural Harmonic Oscillator Differential Equation Because the spring force depends on the. Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. The harmonic oscillator, which we are about to study, has close analogs in many other fields; How to solve harmonic oscillator differential equation: Although we start with a mechanical example of. We wish to solve. Harmonic Oscillator Differential Equation.
From owlcation.com
Solution of Schrödinger Equation for Simple Harmonic Oscillator Owlcation Harmonic Oscillator Differential Equation Although we start with a mechanical example of. We wish to solve the equation of motion for the simple harmonic oscillator: Find the solution in terms. This equation of motion, eq. The harmonic oscillator, which we are about to study, has close analogs in many other fields; Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2}. Harmonic Oscillator Differential Equation.
From www.youtube.com
DSolve, Simple harmonic oscillator SHO Differential equation, Solve Harmonic Oscillator Differential Equation Where k is the spring constant and m is the mass of the oscillating body that is attached to the. The harmonic oscillator, which we are about to study, has close analogs in many other fields; This equation of motion, eq. Simple harmonic oscillator equation (sho). Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0. Harmonic Oscillator Differential Equation.
From www.solutionspile.com
[Solved] Consider the following secondorder differential Harmonic Oscillator Differential Equation The harmonic oscillator, which we are about to study, has close analogs in many other fields; Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Simple harmonic oscillator equation (sho). How to solve harmonic oscillator differential equation: $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Dividing by the mass, this equation can be written in the. Harmonic Oscillator Differential Equation.
From www.youtube.com
Simple Harmonic Oscillator Method its differential equation and Harmonic Oscillator Differential Equation This equation of motion, eq. Simple harmonic oscillator equation (sho). How to solve harmonic oscillator differential equation: Where k is the spring constant and m is the mass of the oscillating body that is attached to the. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ The harmonic oscillator, which we are about to study, has close analogs in many other fields; Explore the. Harmonic Oscillator Differential Equation.
From www.youtube.com
Three Solutions for a Simple Harmonic Oscillator (with initial Harmonic Oscillator Differential Equation Simple harmonic oscillator equation (sho). Although we start with a mechanical example of. We wish to solve the equation of motion for the simple harmonic oscillator: Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}}. Harmonic Oscillator Differential Equation.
From www.youtube.com
Review Harmonic Oscillator Differential Equation YouTube Harmonic Oscillator Differential Equation Simple harmonic oscillator equation (sho). Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Although we start with a mechanical example of. Because the spring force depends on the. We wish to solve the equation of motion for the simple harmonic oscillator: Where k is the. Harmonic Oscillator Differential Equation.
From www.numerade.com
SOLVED 21 Which of the following is a differential equation that Harmonic Oscillator Differential Equation Although we start with a mechanical example of. Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. Because the spring force depends on the. This equation of motion, eq. Where k is the spring constant and m is the mass of the oscillating body that is attached to the. Dividing by. Harmonic Oscillator Differential Equation.
From www.youtube.com
Forced Harmonic Motion (Damped Forced Harmonic Oscillator Differential Harmonic Oscillator Differential Equation Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. This equation of motion, eq. Simple harmonic oscillator equation (sho). Where k is the spring constant and m is the mass of the oscillating body that. Harmonic Oscillator Differential Equation.
From www.scribd.com
Differential Equations Driven Simple Harmonic Oscillator Amplitude Harmonic Oscillator Differential Equation Simple harmonic oscillator equation (sho). Where k is the spring constant and m is the mass of the oscillating body that is attached to the. We wish to solve the equation of motion for the simple harmonic oscillator: Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. The harmonic oscillator, which. Harmonic Oscillator Differential Equation.
From www.youtube.com
Differential Equations of Simple Harmonic Motion YouTube Harmonic Oscillator Differential Equation $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Learn how to derive the differential equation for simple harmonic motion using newton's second law and hooke's law. Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Where k is the spring constant and m is the mass of the oscillating body that is attached to the. Dividing. Harmonic Oscillator Differential Equation.
From tikz.net
differential equations Harmonic Oscillator Differential Equation Where k is the spring constant and m is the mass of the oscillating body that is attached to the. Explore the kinematics and dynamics of mass. Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. How to solve harmonic oscillator differential equation: We wish to solve the equation of motion for the. Harmonic Oscillator Differential Equation.
From slidetodoc.com
Classical Harmonic Oscillator Let us consider a particle Harmonic Oscillator Differential Equation This equation of motion, eq. We wish to solve the equation of motion for the simple harmonic oscillator: Explore the kinematics and dynamics of mass. Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Find the solution in terms. Simple harmonic oscillator equation (sho). Because the. Harmonic Oscillator Differential Equation.
From psadojoe.weebly.com
Harmonic oscillator equation psadojoe Harmonic Oscillator Differential Equation Find the solution in terms. Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Where k is the spring constant and m is the mass of the oscillating body that. Harmonic Oscillator Differential Equation.
From www.youtube.com
Simple Harmonic Motion in Differential Equations YouTube Harmonic Oscillator Differential Equation We wish to solve the equation of motion for the simple harmonic oscillator: How to solve harmonic oscillator differential equation: Simple harmonic oscillator equation (sho). Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Where k is the spring constant and m is the mass of. Harmonic Oscillator Differential Equation.
From mungfali.com
Harmonic Oscillator Differential Equation Harmonic Oscillator Differential Equation Simple harmonic oscillator equation (sho). We wish to solve the equation of motion for the simple harmonic oscillator: This equation of motion, eq. Although we start with a mechanical example of. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Dividing by the mass, this equation can be written in the form \[\ddot{x}+\omega^{2} x=0 \nonumber \] where \[\omega=\sqrt{\dfrac{k}{m}} \nonumber \] this is the. Learn. Harmonic Oscillator Differential Equation.
From www.numerade.com
SOLVED Consider the secondorder differential equation for a simple Harmonic Oscillator Differential Equation The harmonic oscillator, which we are about to study, has close analogs in many other fields; How to solve harmonic oscillator differential equation: Learn how to model simple harmonic motion using newton's 2nd law and the equation of motion. Find the solution in terms. Where k is the spring constant and m is the mass of the oscillating body that. Harmonic Oscillator Differential Equation.
From www.reddit.com
How do you get this solution to the simple harmonic oscillator Harmonic Oscillator Differential Equation This equation of motion, eq. Explore the kinematics and dynamics of mass. Simple harmonic oscillator equation (sho). Because the spring force depends on the. The harmonic oscillator, which we are about to study, has close analogs in many other fields; How to solve harmonic oscillator differential equation: $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Learn how to derive the differential equation for. Harmonic Oscillator Differential Equation.
From www.slideserve.com
PPT Lecture 2 Differential equations PowerPoint Presentation, free Harmonic Oscillator Differential Equation We wish to solve the equation of motion for the simple harmonic oscillator: Simple harmonic oscillator equation (sho). Where k is the spring constant and m is the mass of the oscillating body that is attached to the. Although we start with a mechanical example of. Learn how to model simple harmonic motion using newton's 2nd law and the equation. Harmonic Oscillator Differential Equation.