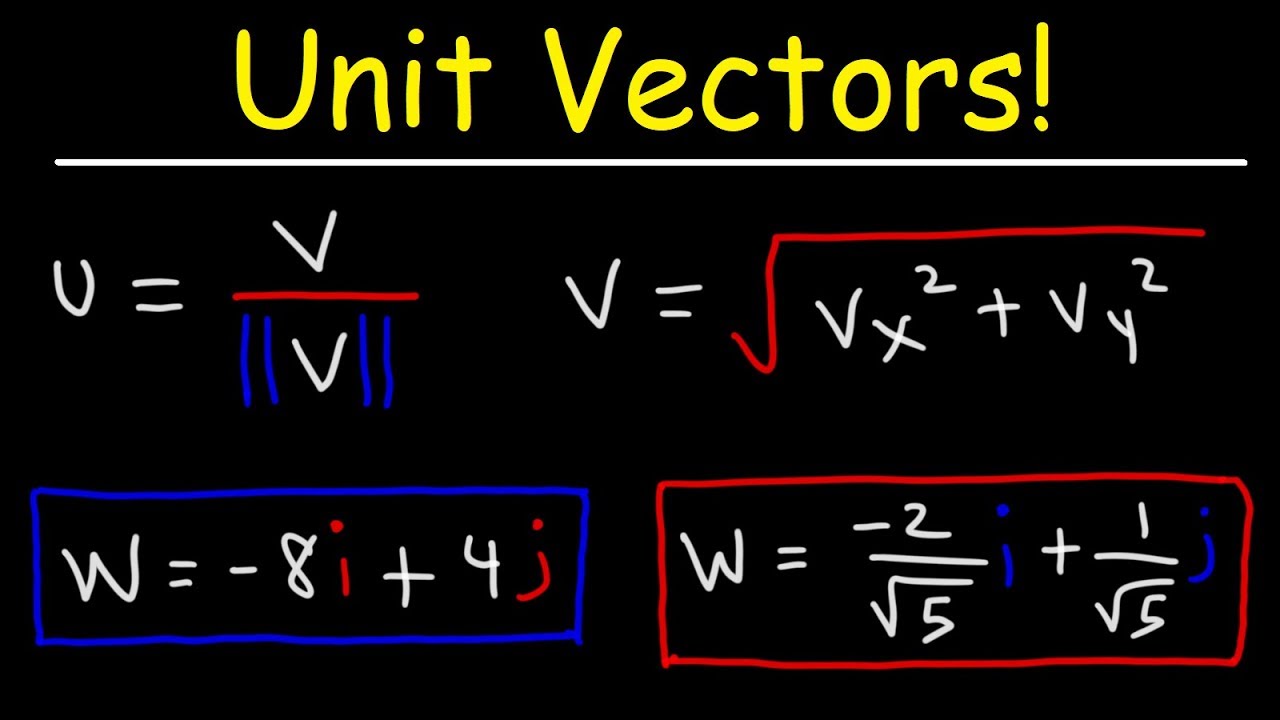
Unit Circle Normal Vector . R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. Unit tangent vector and principal unit normal vector. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. Prove that the rightward pointing unit. The osculating circle is tangent to a curve at a point. Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$ z^2$ = $9$. This means a normal vector of a curve at a given point is perpendicular to the tangent. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as.
from www.youtube.com
The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. Unit tangent vector and principal unit normal vector. This means a normal vector of a curve at a given point is perpendicular to the tangent. Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$ z^2$ = $9$. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. The osculating circle is tangent to a curve at a point. R(t) is a vector function that defines a smooth graph, then at each point a unit tangent.
How To Find The Unit Vector YouTube
Unit Circle Normal Vector Prove that the rightward pointing unit. Unit tangent vector and principal unit normal vector. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$ z^2$ = $9$. The osculating circle is tangent to a curve at a point. R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. This means a normal vector of a curve at a given point is perpendicular to the tangent. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. Prove that the rightward pointing unit. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector.
From www.kristakingmath.com
How to find the unit tangent and unit normal vectors of a vector Unit Circle Normal Vector The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. This means a normal vector of a curve at a given point is perpendicular to the tangent. Prove that the rightward pointing unit. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t. Unit Circle Normal Vector.
From greenemath.com
Unit Circle Lesson Unit Circle Normal Vector The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as. Unit tangent vector and principal unit normal vector. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. The osculating circle is tangent to a. Unit Circle Normal Vector.
From www.shutterstock.com
Unit Circle Mathematics Stock Vector (Royalty Free) 2128084778 Unit Circle Normal Vector The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. Unit tangent vector and principal unit normal vector. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero. Unit Circle Normal Vector.
From www.youtube.com
Video 3025 Unit tangent vector, unit normal vector, of an ellipse Unit Circle Normal Vector The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. R(t) is a vector function that defines a smooth graph, then at each point a unit tangent.. Unit Circle Normal Vector.
From www.youtube.com
Determining the Unit Normal Vector to a Curve Given by a Vector Unit Circle Normal Vector The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. This means a normal vector of a curve at a given point is perpendicular to the tangent. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. Prove that the rightward pointing. Unit Circle Normal Vector.
From commons.wikimedia.org
FileUnit circle angles color.svg Wikimedia Commons Unit Circle Normal Vector Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. The osculating circle is tangent to a curve at a point. Assume $s_1$ be the disk in the $ y =. Unit Circle Normal Vector.
From philschatz.com
Unit Circle · Algebra and Trigonometry Unit Circle Normal Vector This means a normal vector of a curve at a given point is perpendicular to the tangent. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. Unit tangent vector and. Unit Circle Normal Vector.
From thetoptutors.blogspot.com
How To Find Unit Normal Vector Unit Circle Normal Vector The osculating circle is tangent to a curve at a point. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec. Unit Circle Normal Vector.
From www.youtube.com
unit tangent and unit normal vectors (KristaKingMath) YouTube Unit Circle Normal Vector Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$ z^2$ = $9$.. Unit Circle Normal Vector.
From www.youtube.com
Visualizing the Unit Tangent and Principal Normal Vectors YouTube Unit Circle Normal Vector R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. Prove that the rightward pointing unit. Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the. Unit Circle Normal Vector.
From adeelmuirenn.blogspot.com
22+ principal normal vector calculator AdeelMuirenn Unit Circle Normal Vector The osculating circle is tangent to a curve at a point. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec. Unit Circle Normal Vector.
From mathsux.org
The Unit Circle Algebra 2/Trig. Math Lessons Unit Circle Normal Vector R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. Unit tangent vector and principal unit normal vector. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. Prove that the rightward pointing unit. The unit normal vector is defined to be, \[\vec n\left( t \right). Unit Circle Normal Vector.
From themathematicsmaster.com
Unit Circle The Mathematics Master Unit Circle Normal Vector This means a normal vector of a curve at a given point is perpendicular to the tangent. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The unit vector obtained by normalizing the normal. Unit Circle Normal Vector.
From www.mometrix.com
Unit Circles and Standard Position (Video & Practice Questions) Unit Circle Normal Vector The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. Prove that the rightward pointing unit. R(t) is a vector function that defines a smooth graph, then at each point a. Unit Circle Normal Vector.
From www.cuemath.com
Unit Circle Equation of a Unit Circle Unit Circle Chart Unit Circle Normal Vector A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$ z^2$ = $9$. The unit vector. Unit Circle Normal Vector.
From www.shutterstock.com
Unit Circle Angles Stock Vector (Royalty Free) 1102065353 Shutterstock Unit Circle Normal Vector Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$ z^2$ = $9$. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as. Unit tangent vector and principal unit normal vector. The unit. Unit Circle Normal Vector.
From www.youtube.com
Determining a Unit Normal Vector to a Surface YouTube Unit Circle Normal Vector A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. Unit tangent vector and principal unit normal vector. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as. The frenet frame of reference is. Unit Circle Normal Vector.
From etc.usf.edu
Unit Circle Labeled At Special Angles ClipArt ETC Unit Circle Normal Vector The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The osculating circle is tangent to a curve at a point. This means a normal vector of a curve at. Unit Circle Normal Vector.
From www.youtube.com
Defining the Principal Unit Normal Vector YouTube Unit Circle Normal Vector Unit tangent vector and principal unit normal vector. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as. The osculating circle. Unit Circle Normal Vector.
From science.howstuffworks.com
How to Use the Unit Circle in Trigonometry HowStuffWorks Unit Circle Normal Vector The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The osculating circle is. Unit Circle Normal Vector.
From etc.usf.edu
Unit Circle Labeled With Quadrantal Angles And Values ClipArt ETC Unit Circle Normal Vector Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. The osculating circle is tangent to a curve at a point. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The frenet frame of reference is formed by the unit tangent vector, the principal. Unit Circle Normal Vector.
From www.youtube.com
How To Find The Unit Vector YouTube Unit Circle Normal Vector The osculating circle is tangent to a curve at a point. Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$ z^2$ = $9$. R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. Find the unit normal vector for the vector valued function. Unit Circle Normal Vector.
From www.geeksforgeeks.org
How to use the Unit Circle in Trigonometry? Unit Circle Normal Vector Prove that the rightward pointing unit. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t. Unit Circle Normal Vector.
From math.libretexts.org
2.3 Curvature and Normal Vectors of a Curve Mathematics LibreTexts Unit Circle Normal Vector This means a normal vector of a curve at a given point is perpendicular to the tangent. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. Prove that the rightward pointing unit. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by. Unit Circle Normal Vector.
From calculator-online.net
Unit Vector Calculator Find normal vector magnitude & direction Unit Circle Normal Vector The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as. This means a normal vector of a curve at a given point is perpendicular to the tangent. R(t) is a vector function that defines a smooth graph, then at each point a. Unit Circle Normal Vector.
From www.youtube.com
Unit Tangent Vector and Principal Unit Normal Vector YouTube Unit Circle Normal Vector Unit tangent vector and principal unit normal vector. The osculating circle is tangent to a curve at a point. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal. Unit Circle Normal Vector.
From mathsathome.com
How to Find a Vector Perpendicular to a Plane Unit Circle Normal Vector The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector.. Unit Circle Normal Vector.
From freesvg.org
Unit circle Free SVG Unit Circle Normal Vector The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as. Prove that the rightward pointing unit. R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. Assume $s_1$ be the disk in the $ y. Unit Circle Normal Vector.
From daisya-images.blogspot.com
Unit Circle Quadrants Labeled Quadrants 14 Coordinates on the Unit Unit Circle Normal Vector This means a normal vector of a curve at a given point is perpendicular to the tangent. The osculating circle is tangent to a curve at a point. Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$ z^2$ = $9$. The unit normal vector is defined to be, \[\vec n\left(. Unit Circle Normal Vector.
From etc.usf.edu
Unit Circle Labeled With Special Angles And Values ClipArt ETC Unit Circle Normal Vector Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$ z^2$ = $9$. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t. Unit Circle Normal Vector.
From www.youtube.com
Find a Unit Normal Vector to 4x + 12y + 3z = 0 at (0,0,0) YouTube Unit Circle Normal Vector The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as. This means a normal vector of a curve at a given point is perpendicular to the tangent. The frenet frame of reference is formed by the unit tangent vector, the principal unit. Unit Circle Normal Vector.
From www.geeksforgeeks.org
Unit Circle Definition, Formula, Diagram and Solved Examples Unit Circle Normal Vector A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. Unit tangent vector and principal unit normal vector. The frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector. The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero. Unit Circle Normal Vector.
From classful.com
Unit Circle Diagrams Classful Unit Circle Normal Vector A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. This means a normal vector of a curve at a given point is perpendicular to the tangent. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. R(t) is a vector function that defines a. Unit Circle Normal Vector.
From www.youtube.com
Proving the Unit Normal Vector Formula YouTube Unit Circle Normal Vector R(t) is a vector function that defines a smooth graph, then at each point a unit tangent. The unit normal vector is defined to be, \[\vec n\left( t \right) = \frac{{\vec t'\left( t \right)}}{{\left\| {\vec t'\left( t \right)} \right\|}}\]. Prove that the rightward pointing unit. This means a normal vector of a curve at a given point is perpendicular to. Unit Circle Normal Vector.
From www.youtube.com
Unit vector along radial and tangential direction in circular motion Unit Circle Normal Vector A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. Find the unit normal vector for the vector valued function \[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]. Prove that the rightward pointing unit. Assume $s_1$ be the disk in the $ y = 1$ plane bounded by the circle $ x^2$ +$. Unit Circle Normal Vector.