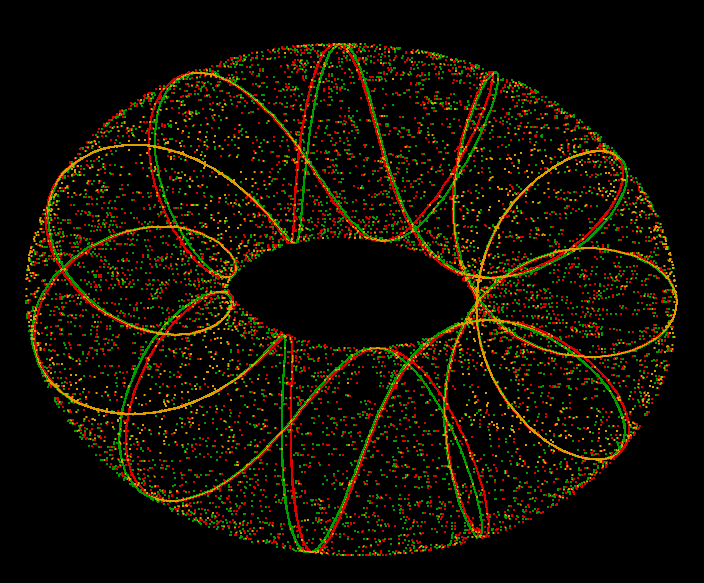
Geodesics Of A Torus . $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. There are meridians, which are cirlces going the short way around. There are a few types of geodesics on a torus of revolution. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. The position on a torus may be specified by the toroidal and poloidal coordinates. The toroidal component is the angle following a large circle around the torus. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. Describe the geodesics on torus. We take a look at the curvature on a torus, and the various forms that geodesics can have. These are compared to the geodesics on a “flat torus”. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from.
from virtualmathmuseum.org
First fundamental form for torus is $$b^2 du^2 + (a+b \cos. Describe the geodesics on torus. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. The toroidal component is the angle following a large circle around the torus. There are a few types of geodesics on a torus of revolution. There are meridians, which are cirlces going the short way around. The position on a torus may be specified by the toroidal and poloidal coordinates. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. These are compared to the geodesics on a “flat torus”.
Torus
Geodesics Of A Torus $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. These are compared to the geodesics on a “flat torus”. There are meridians, which are cirlces going the short way around. Describe the geodesics on torus. There are a few types of geodesics on a torus of revolution. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. We take a look at the curvature on a torus, and the various forms that geodesics can have. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. The toroidal component is the angle following a large circle around the torus. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. The position on a torus may be specified by the toroidal and poloidal coordinates.
From virtualmathmuseum.org
Torus Geodesics Of A Torus Describe the geodesics on torus. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. We take a look at the curvature on a torus, and the various forms that geodesics can have. The toroidal component is the angle following a large circle around the. Geodesics Of A Torus.
From www.researchgate.net
Systolic geodesics on the torus with a hole removed. The hole is a Geodesics Of A Torus The toroidal component is the angle following a large circle around the torus. The position on a torus may be specified by the toroidal and poloidal coordinates. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. There are a few types of geodesics on. Geodesics Of A Torus.
From github.com
GitHub HarishNani45/GeodesicsonTorus simulation of Geodesics on Geodesics Of A Torus Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. The toroidal component is the angle following a large circle around the torus. The position on a torus may be specified by the toroidal and poloidal coordinates. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin. Geodesics Of A Torus.
From virtualmathmuseum.org
Torus Geodesics Of A Torus Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. These are compared to the geodesics on a “flat torus”. Geodesics on the torus corresponds to a discrete set of energy levels in this. Geodesics Of A Torus.
From www.researchgate.net
Various modalities of toroidal geometry (A) Nested torus structure (B Geodesics Of A Torus There are a few types of geodesics on a torus of revolution. These are compared to the geodesics on a “flat torus”. The toroidal component is the angle following a large circle around the torus. There are meridians, which are cirlces going the short way around. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. Geodesic oscillates. Geodesics Of A Torus.
From www.researchgate.net
An closed geodesic [7, 1; 1] for the unit ring torus with 7 loops Geodesics Of A Torus The position on a torus may be specified by the toroidal and poloidal coordinates. There are meridians, which are cirlces going the short way around. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. The toroidal component is the angle following a large circle around the. Geodesics Of A Torus.
From nbodyphysics.com
Asteroids on a Torus Nbody Physics Geodesics Of A Torus First fundamental form for torus is $$b^2 du^2 + (a+b \cos. Describe the geodesics on torus. The position on a torus may be specified by the toroidal and poloidal coordinates. There are meridians, which are cirlces going the short way around. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization. Geodesics Of A Torus.
From thatsmaths.com
Curvature and Geodesics on a Torus ThatsMaths Geodesics Of A Torus Describe the geodesics on torus. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. There are a few types of geodesics on a torus of revolution. The position on a torus may be specified by the toroidal and poloidal coordinates. Geodesic oscillates around the outside. Geodesics Of A Torus.
From www.youtube.com
Simulation of a Geodesic on a TORUS in Python YouTube Geodesics Of A Torus We take a look at the curvature on a torus, and the various forms that geodesics can have. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. The position on a torus may be specified by the toroidal and poloidal coordinates. There are meridians, which. Geodesics Of A Torus.
From www.researchgate.net
The approximate geodesics computed by the DLA (left) and FMM (right Geodesics Of A Torus Describe the geodesics on torus. The position on a torus may be specified by the toroidal and poloidal coordinates. These are compared to the geodesics on a “flat torus”. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. There are a few types of geodesics on a torus of revolution. Geodesic oscillates around the outside equator of the. Geodesics Of A Torus.
From www.semanticscholar.org
Figure 1 from Geodesics on the Torus and other Surfaces of Revolution Geodesics Of A Torus The position on a torus may be specified by the toroidal and poloidal coordinates. There are meridians, which are cirlces going the short way around. We take a look at the curvature on a torus, and the various forms that geodesics can have. The toroidal component is the angle following a large circle around the torus. First fundamental form for. Geodesics Of A Torus.
From mathmonks.com
Torus Shape Definition, Examples, and Diagrams Geodesics Of A Torus Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. Describe the geodesics on torus. There are meridians, which are cirlces going the short way around. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization. Geodesics Of A Torus.
From math.stackexchange.com
geometry Geodesics on torus Mathematics Stack Exchange Geodesics Of A Torus These are compared to the geodesics on a “flat torus”. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. There are a few types of geodesics on a torus of revolution. The toroidal. Geodesics Of A Torus.
From virtualmathmuseum.org
Torus Geodesics Of A Torus These are compared to the geodesics on a “flat torus”. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. The toroidal component is the angle following a large circle around the torus. The position on a torus may be specified by the toroidal and poloidal. Geodesics Of A Torus.
From www.researchgate.net
Geodesic Bézier curve on torus. Download Scientific Diagram Geodesics Of A Torus The toroidal component is the angle following a large circle around the torus. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$.. Geodesics Of A Torus.
From www.researchgate.net
The closed geodesics on the unit ring torus with initial angles 0 ≤ β 0 Geodesics Of A Torus There are meridians, which are cirlces going the short way around. These are compared to the geodesics on a “flat torus”. Describe the geodesics on torus. The toroidal component is the angle following a large circle around the torus. There are a few types of geodesics on a torus of revolution. Geodesics on the torus corresponds to a discrete set. Geodesics Of A Torus.
From virtualmathmuseum.org
Torus Geodesics Of A Torus There are a few types of geodesics on a torus of revolution. The toroidal component is the angle following a large circle around the torus. Describe the geodesics on torus. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. First fundamental form for torus is. Geodesics Of A Torus.
From www.researchgate.net
Homotopy geodesic on 3hole torus 3. Download Scientific Diagram Geodesics Of A Torus These are compared to the geodesics on a “flat torus”. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. There are a few types of geodesics on a torus of revolution. The toroidal component is the angle following a large circle around the torus. Geodesics on the torus corresponds to a discrete set of energy levels in this. Geodesics Of A Torus.
From virtualmathmuseum.org
Torus Geodesics Of A Torus These are compared to the geodesics on a “flat torus”. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. Geodesics on the torus corresponds to a discrete set of energy levels in this. Geodesics Of A Torus.
From virtualmathmuseum.org
Torus Geodesics Of A Torus These are compared to the geodesics on a “flat torus”. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. The position on a torus may be specified by the toroidal and poloidal coordinates. We take a look at the curvature on a torus, and the various forms that geodesics can have. Describe the geodesics on torus. The. Geodesics Of A Torus.
From www.researchgate.net
Conditionally maximin design on the surface of a torus. The distance Geodesics Of A Torus Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. The toroidal component is the angle following a large circle around the torus. We take a look at the curvature on a torus, and the various forms that geodesics can have. Geodesic oscillates around the outside. Geodesics Of A Torus.
From www.researchgate.net
Geodesic between framed spirals on a torus of revolution. Each framed Geodesics Of A Torus First fundamental form for torus is $$b^2 du^2 + (a+b \cos. There are meridians, which are cirlces going the short way around. There are a few types of geodesics on a torus of revolution. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. The position on a torus may be specified by the toroidal and poloidal coordinates.. Geodesics Of A Torus.
From people.math.harvard.edu
Geodesics on torus of revolution Geodesics Of A Torus Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. Describe the geodesics on torus. The position on a torus may be specified by the toroidal and poloidal coordinates. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙. Geodesics Of A Torus.
From mathmonks.com
Torus Shape Definition, Examples, and Diagrams Geodesics Of A Torus These are compared to the geodesics on a “flat torus”. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. The toroidal. Geodesics Of A Torus.
From people.math.harvard.edu
Geodesics on torus of revolution Geodesics Of A Torus First fundamental form for torus is $$b^2 du^2 + (a+b \cos. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. The toroidal component is the angle following a large circle around the torus.. Geodesics Of A Torus.
From people.math.harvard.edu
Geodesics on torus of revolution Geodesics Of A Torus The position on a torus may be specified by the toroidal and poloidal coordinates. There are a few types of geodesics on a torus of revolution. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. These are compared to the geodesics on a “flat torus”. Describe the geodesics on torus. Geodesic oscillates around the outside equator of the. Geodesics Of A Torus.
From www.researchgate.net
Geodesic vectors (straightest geodesics) on a torus model. The angle Geodesics Of A Torus There are meridians, which are cirlces going the short way around. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between. Geodesics Of A Torus.
From www.researchgate.net
Swiss cross presentation of the torus with a boundary. The vertical Geodesics Of A Torus Describe the geodesics on torus. $$\sigma (u,v)= ( (a+b \cos u)\cos v, (a+b\cos u)\sin v, b\sin u)$$. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous. Geodesics Of A Torus.
From www.scribd.com
The Curvature and Geodesics of The Torus PDF Geometry Geodesics Of A Torus First fundamental form for torus is $$b^2 du^2 + (a+b \cos. There are a few types of geodesics on a torus of revolution. Describe the geodesics on torus. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization of energy levels in the. These are compared to the geodesics on a. Geodesics Of A Torus.
From www.pngwing.com
Geodesic dome Geometry Torus Mathematics, Mathematics, triangle, sphere Geodesics Of A Torus There are meridians, which are cirlces going the short way around. First fundamental form for torus is $$b^2 du^2 + (a+b \cos. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. We take a look at the curvature on a torus, and the various. Geodesics Of A Torus.
From demonstrations.wolfram.com
Geodesics of a Torus Solved with a Method of Lagrange Wolfram Geodesics Of A Torus There are a few types of geodesics on a torus of revolution. The toroidal component is the angle following a large circle around the torus. The position on a torus may be specified by the toroidal and poloidal coordinates. These are compared to the geodesics on a “flat torus”. Geodesic oscillates around the outside equator of the torus with ϕ. Geodesics Of A Torus.
From www.researchgate.net
A toroidal surface of radius r and its coordinate system (θ,ϕ,ρ). R0 is Geodesics Of A Torus The toroidal component is the angle following a large circle around the torus. Describe the geodesics on torus. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the. Geodesics Of A Torus.
From angyansheng.github.io
My Final Year Project (I) Counting Geodesics · Yan Sheng's site Geodesics Of A Torus Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. These are compared to the geodesics on a “flat torus”. We take a look at the curvature on a torus, and the various forms that geodesics can have. There are meridians, which are cirlces going. Geodesics Of A Torus.
From studylib.net
Torus Geodesics Geodesics Of A Torus First fundamental form for torus is $$b^2 du^2 + (a+b \cos. There are a few types of geodesics on a torus of revolution. We take a look at the curvature on a torus, and the various forms that geodesics can have. Geodesics on the torus corresponds to a discrete set of energy levels in this picture, mirroring the analogous quantization. Geodesics Of A Torus.
From math.stackexchange.com
differential geometry Geodesics on torus Mathematics Stack Exchange Geodesics Of A Torus There are a few types of geodesics on a torus of revolution. Geodesic oscillates around the outside equator of the torus with ϕ oscillating between ±ϕ 0 while θ˙ remains of fixed sign and bounded away from. Describe the geodesics on torus. There are meridians, which are cirlces going the short way around. First fundamental form for torus is $$b^2. Geodesics Of A Torus.