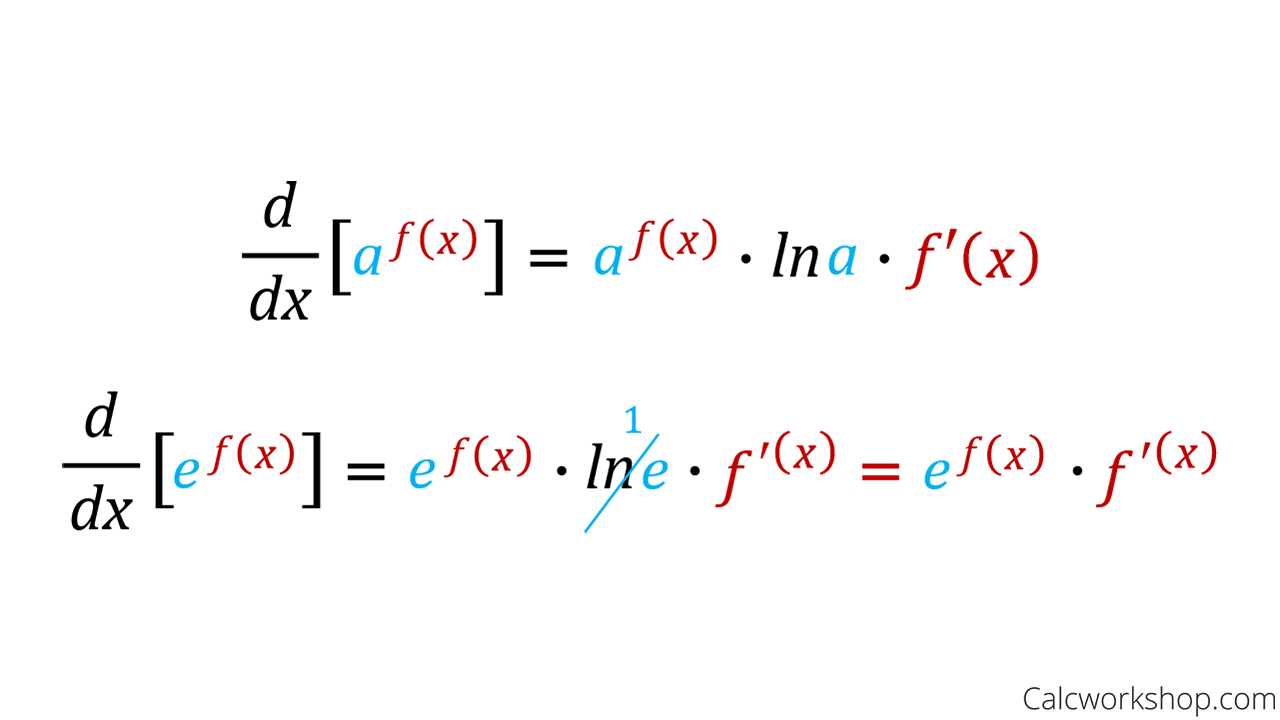Derivatives And Integrals Of Exponential Functions . The derivative and integral of the exponential function is shared under a not declared. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. this page titled 4.5: we begin the section by defining the natural logarithm in terms of an integral. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. recognize the derivative and integral of the exponential function. use the derivative of the natural exponential function, the quotient rule, and the chain rule. Prove properties of logarithms and exponential functions using integrals. This definition forms the foundation for the.
from calcworkshop.com
This definition forms the foundation for the. we begin the section by defining the natural logarithm in terms of an integral. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. The derivative and integral of the exponential function is shared under a not declared. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. Prove properties of logarithms and exponential functions using integrals. exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. use the derivative of the natural exponential function, the quotient rule, and the chain rule. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. this page titled 4.5:
Derivative of Exponential Function
Derivatives And Integrals Of Exponential Functions in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. this page titled 4.5: although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. we begin the section by defining the natural logarithm in terms of an integral. The derivative and integral of the exponential function is shared under a not declared. This definition forms the foundation for the. recognize the derivative and integral of the exponential function. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. Prove properties of logarithms and exponential functions using integrals. use the derivative of the natural exponential function, the quotient rule, and the chain rule.
From mymathware.blogspot.com
Calculus Integration of Exponential Functions Derivatives And Integrals Of Exponential Functions recognize the derivative and integral of the exponential function. use the derivative of the natural exponential function, the quotient rule, and the chain rule. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. although the derivative represents a rate of change or a growth. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Exponential Function Derivatives & Integrals YouTube Derivatives And Integrals Of Exponential Functions The derivative and integral of the exponential function is shared under a not declared. exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. recognize the derivative and integral of the exponential function. use the derivative of the natural exponential function, the quotient rule, and the chain rule. Prove properties of logarithms. Derivatives And Integrals Of Exponential Functions.
From www.docsity.com
Integrals of Exponential Functions Lecture notes Engineering Derivatives And Integrals Of Exponential Functions This definition forms the foundation for the. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. use the derivative of the natural exponential function, the quotient rule, and the chain rule. although the derivative represents a rate of change or a growth rate, the integral. Derivatives And Integrals Of Exponential Functions.
From www.slideserve.com
PPT Calculus II Chapter 6 Section 7 Derivatives & Integrals of Derivatives And Integrals Of Exponential Functions The derivative and integral of the exponential function is shared under a not declared. This definition forms the foundation for the. use the derivative of the natural exponential function, the quotient rule, and the chain rule. we begin the section by defining the natural logarithm in terms of an integral. this page titled 4.5: although the. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
DERIVATIVES OF EXPONENTIAL FUNCTIONS YouTube Derivatives And Integrals Of Exponential Functions exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. we begin the section by defining the natural logarithm in terms of an integral. Prove properties of logarithms and. Derivatives And Integrals Of Exponential Functions.
From www.onlinemathlearning.com
Calculus Derivative Rules (formulas, examples, solutions, videos) Derivatives And Integrals Of Exponential Functions recognize the derivative and integral of the exponential function. use the derivative of the natural exponential function, the quotient rule, and the chain rule. This definition forms the foundation for the. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. The derivative and integral of. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Derivatives of Exponential Functions YouTube Derivatives And Integrals Of Exponential Functions exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. Prove properties of logarithms and exponential functions using integrals. we begin the section by defining the natural logarithm in terms of. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Calculus I Integrals of Exponential Functions YouTube Derivatives And Integrals Of Exponential Functions The derivative and integral of the exponential function is shared under a not declared. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a.. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Indefinite Integral of Exponential Functions Calculus YouTube Derivatives And Integrals Of Exponential Functions recognize the derivative and integral of the exponential function. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. The derivative and integral of the exponential function is shared under a not declared. this page titled 4.5: although the derivative represents a rate of change. Derivatives And Integrals Of Exponential Functions.
From www.showme.com
Exponential derivative rules Math ShowMe Derivatives And Integrals Of Exponential Functions recognize the derivative and integral of the exponential function. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. Prove properties of logarithms and exponential functions using integrals. The derivative and integral of the exponential function is shared under a not declared. exponential and. Derivatives And Integrals Of Exponential Functions.
From en.neurochispas.com
Derivatives and Integrals of Exponential Functions Neurochispas Derivatives And Integrals Of Exponential Functions although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. Prove properties of logarithms and exponential functions using integrals. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. The derivative and integral of. Derivatives And Integrals Of Exponential Functions.
From docslib.org
List of Integrals of Exponential Functions 1 List of Integrals of Derivatives And Integrals Of Exponential Functions recognize the derivative and integral of the exponential function. we begin the section by defining the natural logarithm in terms of an integral. this page titled 4.5: in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. This definition forms the foundation for. Derivatives And Integrals Of Exponential Functions.
From study.com
How to Calculate Integrals of Exponential Functions Lesson Derivatives And Integrals Of Exponential Functions use the derivative of the natural exponential function, the quotient rule, and the chain rule. This definition forms the foundation for the. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. Prove properties of logarithms and exponential functions using integrals. recognize the derivative and integral. Derivatives And Integrals Of Exponential Functions.
From www.slideserve.com
PPT Calculus II Chapter 6 Section 7 Derivatives & Integrals of Derivatives And Integrals Of Exponential Functions in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. use the derivative of the natural exponential function, the quotient rule, and the chain rule. although the derivative represents a rate of change or a growth rate, the integral represents the total change or. Derivatives And Integrals Of Exponential Functions.
From www.studocu.com
Derivative and Integral of Exponential Functions MATH 8 For a l Y A Derivatives And Integrals Of Exponential Functions Prove properties of logarithms and exponential functions using integrals. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. we begin the section by defining the natural logarithm in terms of. Derivatives And Integrals Of Exponential Functions.
From www.studypool.com
SOLUTION Integration formula of exponential functions Studypool Derivatives And Integrals Of Exponential Functions use the derivative of the natural exponential function, the quotient rule, and the chain rule. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. Prove properties of logarithms and exponential functions using integrals. recognize the derivative and integral of the exponential function. although the. Derivatives And Integrals Of Exponential Functions.
From calcworkshop.com
Derivative of Exponential Function Derivatives And Integrals Of Exponential Functions This definition forms the foundation for the. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. The derivative and integral of the exponential function is shared under a not declared. we begin the section by defining the natural logarithm in terms of an integral.. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Calculus I Integrals of Exponential Functions YouTube Derivatives And Integrals Of Exponential Functions The derivative and integral of the exponential function is shared under a not declared. use the derivative of the natural exponential function, the quotient rule, and the chain rule. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. although the derivative represents a. Derivatives And Integrals Of Exponential Functions.
From nghs12acc.blogspot.com
core pure 3 notes integrals involving exponentials Derivatives And Integrals Of Exponential Functions this page titled 4.5: although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. use the derivative of the natural exponential function, the quotient rule, and the chain rule. exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. Prove. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Derivatives of EXPONENTIAL functions (full lesson) grade 12 MCV4U Derivatives And Integrals Of Exponential Functions we begin the section by defining the natural logarithm in terms of an integral. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. recognize the derivative and integral of the exponential function. although the derivative represents a rate of change or a growth rate,. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Derivatives of Exponential Functions YouTube Derivatives And Integrals Of Exponential Functions in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. The derivative and integral of the exponential function is shared under a not declared. use the derivative of the natural exponential function, the quotient rule, and the chain rule. exponential and logarithmic functions are. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Example of Derivative Of Exponential Function YouTube Derivatives And Integrals Of Exponential Functions recognize the derivative and integral of the exponential function. This definition forms the foundation for the. we begin the section by defining the natural logarithm in terms of an integral. this page titled 4.5: use the derivative of the natural exponential function, the quotient rule, and the chain rule. exponential and logarithmic functions are used. Derivatives And Integrals Of Exponential Functions.
From www.nagwa.com
Question Video Finding the Derivative of a Function Defined by an Derivatives And Integrals Of Exponential Functions This definition forms the foundation for the. we begin the section by defining the natural logarithm in terms of an integral. recognize the derivative and integral of the exponential function. use the derivative of the natural exponential function, the quotient rule, and the chain rule. although the derivative represents a rate of change or a growth. Derivatives And Integrals Of Exponential Functions.
From youtube.com
Derivatives of Exponential Functions with Base e YouTube Derivatives And Integrals Of Exponential Functions The derivative and integral of the exponential function is shared under a not declared. recognize the derivative and integral of the exponential function. this page titled 4.5: although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. in order to differentiate the exponential function \[f(x). Derivatives And Integrals Of Exponential Functions.
From nghs12acc.blogspot.com
core pure 3 notes integrals involving exponentials Derivatives And Integrals Of Exponential Functions exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. The derivative and integral of the exponential function is shared under a not declared. This definition forms the foundation for the. we begin the section by defining the natural logarithm in terms of an integral. although the derivative represents a rate of. Derivatives And Integrals Of Exponential Functions.
From www.slideserve.com
PPT Aim How do we differentiate and integrate the exponential Derivatives And Integrals Of Exponential Functions The derivative and integral of the exponential function is shared under a not declared. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. we. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Derivative of Exponential Functions YouTube Derivatives And Integrals Of Exponential Functions This definition forms the foundation for the. The derivative and integral of the exponential function is shared under a not declared. this page titled 4.5: although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. exponential and logarithmic functions are used to model population growth, cell. Derivatives And Integrals Of Exponential Functions.
From www.slideserve.com
PPT 5.4 Exponential Functions Differentiation and Integration Derivatives And Integrals Of Exponential Functions recognize the derivative and integral of the exponential function. use the derivative of the natural exponential function, the quotient rule, and the chain rule. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. we begin the section by defining the natural logarithm in terms. Derivatives And Integrals Of Exponential Functions.
From calcworkshop.com
Derivative of Exponential Function (Fully Explained!) Derivatives And Integrals Of Exponential Functions we begin the section by defining the natural logarithm in terms of an integral. The derivative and integral of the exponential function is shared under a not declared. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. although the derivative represents a rate. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
CA.TF.5 Integrating Exponential Functions YouTube Derivatives And Integrals Of Exponential Functions this page titled 4.5: The derivative and integral of the exponential function is shared under a not declared. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. Prove properties of logarithms and exponential functions using integrals. This definition forms the foundation for the. exponential and. Derivatives And Integrals Of Exponential Functions.
From www.studypool.com
SOLUTION derivatives and integrals of exponential functions Studypool Derivatives And Integrals Of Exponential Functions exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Calculus I 5.4.1 Derivatives and Integrals of the Natural Exponential Derivatives And Integrals Of Exponential Functions in order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a. this page titled 4.5: recognize the derivative and integral of the exponential function. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the. Derivatives And Integrals Of Exponential Functions.
From www.youtube.com
Ex 4 Derivatives of Exponential Functions with the Quotient Rule YouTube Derivatives And Integrals Of Exponential Functions The derivative and integral of the exponential function is shared under a not declared. This definition forms the foundation for the. use the derivative of the natural exponential function, the quotient rule, and the chain rule. although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. . Derivatives And Integrals Of Exponential Functions.
From youtube.com
Calculus Derivatives of General Exponential Functions YouTube Derivatives And Integrals Of Exponential Functions we begin the section by defining the natural logarithm in terms of an integral. this page titled 4.5: although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total. The derivative and integral of the exponential function is shared under a not declared. although the derivative. Derivatives And Integrals Of Exponential Functions.
From ella-has-vega.blogspot.com
Integration of Exponential Functions EllahasVega Derivatives And Integrals Of Exponential Functions exponential and logarithmic functions are used to model population growth, cell growth, and financial growth,. use the derivative of the natural exponential function, the quotient rule, and the chain rule. recognize the derivative and integral of the exponential function. we begin the section by defining the natural logarithm in terms of an integral. Prove properties of. Derivatives And Integrals Of Exponential Functions.