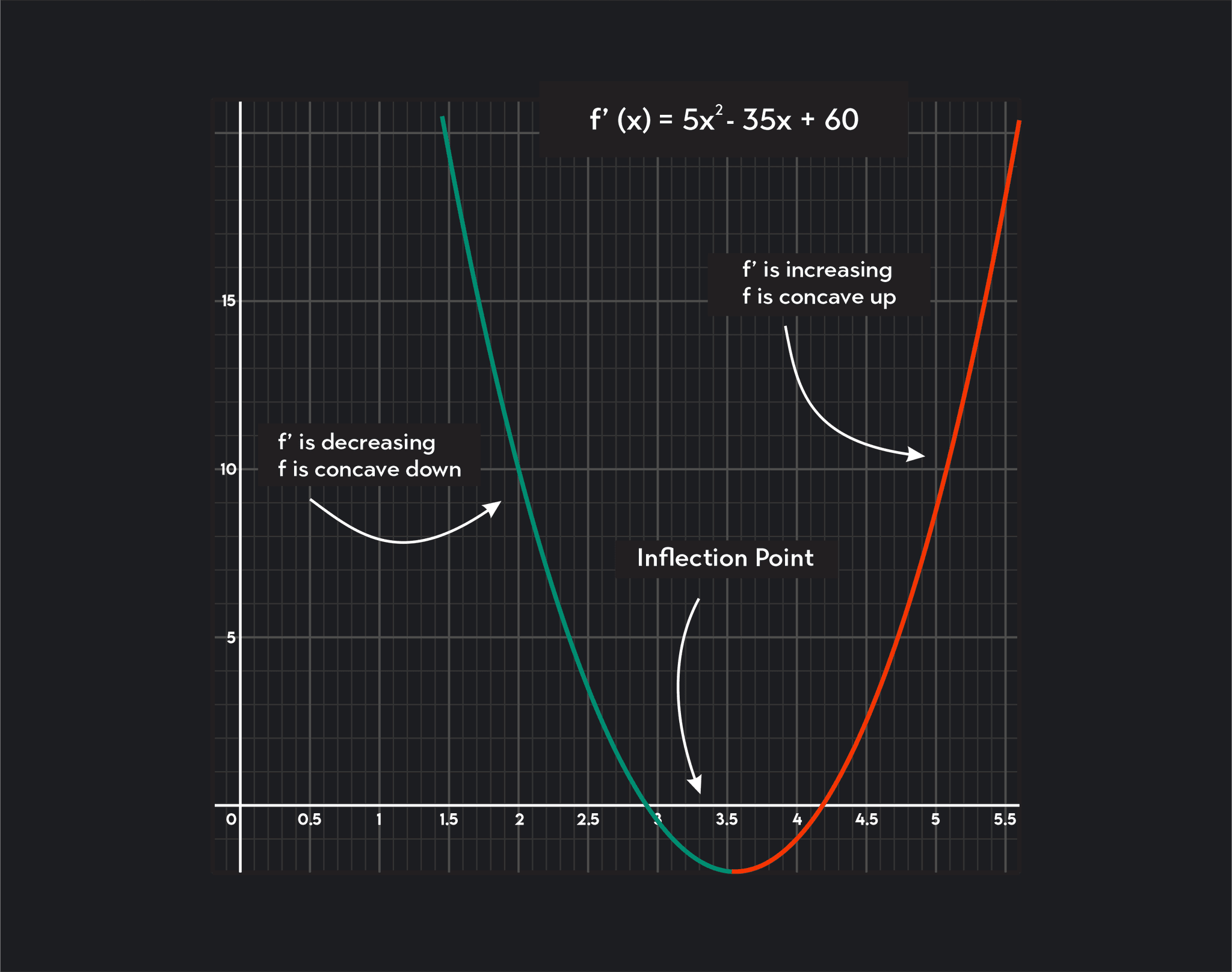
Point Of Inflection Has Tangent . At $ m $ the curve has a unique tangent, and within. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). Inflection points and rates of change. For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. A tangent line always passes through the curve at a double or tangent point. Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). The tangent line of inflection point always passes. You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. In this article, the concept. A point $ m $ on a planar curve having the following properties:
from articles.outlier.org
You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. A tangent line always passes through the curve at a double or tangent point. In this article, the concept. For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. At $ m $ the curve has a unique tangent, and within. Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). Inflection points and rates of change. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. A point $ m $ on a planar curve having the following properties: The tangent line of inflection point always passes.
Inflection Point Definition and How to Find It in 5 Steps Outlier
Point Of Inflection Has Tangent A point $ m $ on a planar curve having the following properties: Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. In this article, the concept. Inflection points and rates of change. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. A point $ m $ on a planar curve having the following properties: A tangent line always passes through the curve at a double or tangent point. The tangent line of inflection point always passes. You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. At $ m $ the curve has a unique tangent, and within.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Has Tangent The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). Inflection points and rates of change. At $ m $ the curve has a unique tangent, and within. In this article, the concept. Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). A tangent line always passes. Point Of Inflection Has Tangent.
From www.youtube.com
Given a Polynomial Function Find Line Tangent To The Graph And x, y Coordinates Of Inflection Point Of Inflection Has Tangent At $ m $ the curve has a unique tangent, and within. You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. Inflection points and rates of change. The point where the function is neither concave nor convex is known as inflection point. Point Of Inflection Has Tangent.
From www.youtube.com
Find point of inflection for trig function tan(x) YouTube Point Of Inflection Has Tangent At $ m $ the curve has a unique tangent, and within. In this article, the concept. The tangent line of inflection point always passes. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. A tangent line always passes through. Point Of Inflection Has Tangent.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Has Tangent For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). In this article, the. Point Of Inflection Has Tangent.
From mungfali.com
Equation Of Tangent Line To Curve Point Of Inflection Has Tangent The tangent line of inflection point always passes. A tangent line always passes through the curve at a double or tangent point. In this article, the concept. Inflection points and rates of change. Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). For all tangents to $y=x^2$, the curve lies entirely. Point Of Inflection Has Tangent.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection Has Tangent The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Inflection points and rates of change. For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). A point $ m $. Point Of Inflection Has Tangent.
From www.numerade.com
Make the curve y=ax^3+bx^2+cx+d pass through ( 0, 3 ) and have at ( 1, 2 ) a point of inflection Point Of Inflection Has Tangent A tangent line always passes through the curve at a double or tangent point. A point $ m $ on a planar curve having the following properties: The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. The tangent line of. Point Of Inflection Has Tangent.
From www.vrogue.co
Inflection Point Definition And How To Find It In 5 S vrogue.co Point Of Inflection Has Tangent The tangent line of inflection point always passes. A point $ m $ on a planar curve having the following properties: In this article, the concept. Inflection points and rates of change. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then. Point Of Inflection Has Tangent.
From www.savemyexams.com
Concavity & Points of Inflection DP IB Maths AA HL Revision Notes 2021 Point Of Inflection Has Tangent At $ m $ the curve has a unique tangent, and within. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). Inflection points and rates of change. For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. You can also think of an inflection point as being where the rate. Point Of Inflection Has Tangent.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Has Tangent Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Inflection points and rates of change. In. Point Of Inflection Has Tangent.
From www.youtube.com
How to Find a Tangent Line of a Function at its Point of Inflection YouTube Point Of Inflection Has Tangent The point where the function is neither concave nor convex is known as inflection point or the point of inflection. A point $ m $ on a planar curve having the following properties: In this article, the concept. Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). For all tangents to. Point Of Inflection Has Tangent.
From www.quora.com
How to find the slope of the tangent line at the point of inflection for x^3 6x^2+4x+8 Quora Point Of Inflection Has Tangent In this article, the concept. For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). At $. Point Of Inflection Has Tangent.
From www.youtube.com
Inflection points from graphs of function & derivatives AP Calculus AB Khan Academy YouTube Point Of Inflection Has Tangent At $ m $ the curve has a unique tangent, and within. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Inflection points and rates of change. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). You can also think of an inflection point. Point Of Inflection Has Tangent.
From owlcation.com
Math How to Find the Tangent Line of a Function in a Point Owlcation Point Of Inflection Has Tangent A point $ m $ on a planar curve having the following properties: At $ m $ the curve has a unique tangent, and within. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. A tangent line always passes through. Point Of Inflection Has Tangent.
From www.numerade.com
SOLVED Make the curve y=ax^3+bx^2+cx+d pass through ( 0, 3 ) and have at ( 1, 2 ) a point of Point Of Inflection Has Tangent At $ m $ the curve has a unique tangent, and within. Inflection points and rates of change. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. A tangent line always passes through the. Point Of Inflection Has Tangent.
From www.alamy.com
Concavity of curve. Inflection point, concave down and concave up. Second derivative tangent Point Of Inflection Has Tangent The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). At $ m $ the curve has a unique tangent, and within. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. A point $ m $ on a planar curve having the following properties: For. Point Of Inflection Has Tangent.
From www.alamy.com
Concavity of curve. Inflection point, concave down and concave up. Second derivative tangent Point Of Inflection Has Tangent At $ m $ the curve has a unique tangent, and within. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). A tangent line always passes through the curve at a double or tangent point. A point $ m $ on a planar curve having the following properties: You can also think of an inflection. Point Of Inflection Has Tangent.
From www.studypool.com
SOLUTION Differential calculus review outline tangents and normal critical points and Point Of Inflection Has Tangent You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. A point $ m $ on a planar curve having the following properties: In this article, the concept. Inflection points and rates of change. At $ m $ the curve has a unique. Point Of Inflection Has Tangent.
From www.youtube.com
How to find point of inflection for tanx analyzing second derivative YouTube Point Of Inflection Has Tangent A tangent line always passes through the curve at a double or tangent point. You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. Inflection points and rates of change. The tangent line of inflection point always passes. The point where the function. Point Of Inflection Has Tangent.
From 28left.github.io
Inflection Points — Penn State Math 110 Companion Site Point Of Inflection Has Tangent A tangent line always passes through the curve at a double or tangent point. The tangent line of inflection point always passes. Inflection points and rates of change. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). A point $ m $ on a planar curve having the following properties: The point where the function. Point Of Inflection Has Tangent.
From www.slideserve.com
PPT Extremum and inflection of point PowerPoint Presentation, free download ID4277880 Point Of Inflection Has Tangent A point $ m $ on a planar curve having the following properties: Inflection points and rates of change. In this article, the concept. A tangent line always passes through the curve at a double or tangent point. The tangent line of inflection point always passes. For all tangents to $y=x^2$, the curve lies entirely on one side of the. Point Of Inflection Has Tangent.
From copyprogramming.com
Inflection point, understanding problem Point Of Inflection Has Tangent A point $ m $ on a planar curve having the following properties: Inflection points and rates of change. A tangent line always passes through the curve at a double or tangent point. The tangent line of inflection point always passes. You can also think of an inflection point as being where the rate of change of the slope changes. Point Of Inflection Has Tangent.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Has Tangent A tangent line always passes through the curve at a double or tangent point. In this article, the concept. The tangent line of inflection point always passes. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed. Point Of Inflection Has Tangent.
From irevise.com
Advanced Trigonometry 1 Stationary Points, Curve Sketching, Points of Inflection Notes Point Of Inflection Has Tangent You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. The tangent line of inflection point always passes. A point $ m $ on a planar curve having the following properties: The horizontal inflection point (orange circle) has a horizontal tangent line (orange. Point Of Inflection Has Tangent.
From www.alamy.com
Concavity of curve. Inflection point, concave down and concave up. Second derivative tangent Point Of Inflection Has Tangent A tangent line always passes through the curve at a double or tangent point. At $ m $ the curve has a unique tangent, and within. Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). The tangent line of inflection point always passes. In this article, the concept. Inflection points and. Point Of Inflection Has Tangent.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection Has Tangent The point where the function is neither concave nor convex is known as inflection point or the point of inflection. The horizontal inflection point (orange circle) has a horizontal tangent line (orange dashed line). Inflection points and rates of change. For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. A point $ m $. Point Of Inflection Has Tangent.
From www.alamy.com
Concavity of curve. Inflection point, concave down and concave up. Second derivative tangent Point Of Inflection Has Tangent In this article, the concept. A point $ m $ on a planar curve having the following properties: A tangent line always passes through the curve at a double or tangent point. You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. Inflection. Point Of Inflection Has Tangent.
From favpng.com
Plane Curve Inflection Point Tangent, PNG, 845x648px, Curve, Area, Brand, Concave Function Point Of Inflection Has Tangent At $ m $ the curve has a unique tangent, and within. A point $ m $ on a planar curve having the following properties: Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). A tangent line always passes through the curve at a double or tangent point. The horizontal inflection. Point Of Inflection Has Tangent.
From www.slideserve.com
PPT Graphs of Tangent & Cotangent PowerPoint Presentation, free download ID1223820 Point Of Inflection Has Tangent At $ m $ the curve has a unique tangent, and within. You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. A point $ m $ on a planar curve having the following properties: Let $f(x)$ be the function, $l(x)$ be the. Point Of Inflection Has Tangent.
From slideplayer.com
53 Day 1 connecting f graphs with f' and f" graphs ppt download Point Of Inflection Has Tangent At $ m $ the curve has a unique tangent, and within. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. The tangent line of inflection point always passes. A point $ m $. Point Of Inflection Has Tangent.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Has Tangent Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). At $ m $ the curve has a unique tangent, and within. A point $ m $ on a planar curve having the following properties: The point where the function is neither concave nor convex is known as inflection point or the. Point Of Inflection Has Tangent.
From www.youtube.com
Find equation of tangent line at point of inflection for a polynomial function. YouTube Point Of Inflection Has Tangent You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. A point $ m $ on a planar curve having the following properties: For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. The point where the function. Point Of Inflection Has Tangent.
From www.youtube.com
Tangent Line Estimates and Points of Inflection pg 6 YouTube Point Of Inflection Has Tangent A tangent line always passes through the curve at a double or tangent point. In this article, the concept. A point $ m $ on a planar curve having the following properties: For all tangents to $y=x^2$, the curve lies entirely on one side of the tangent. Inflection points and rates of change. You can also think of an inflection. Point Of Inflection Has Tangent.
From www.dreamstime.com
Inflection Point on Graph of Function. Stock Vector Illustration of icon, mathematical 259651303 Point Of Inflection Has Tangent You can also think of an inflection point as being where the rate of change of the slope changes from increasing to decreasing, or increasing to decreasing. In this article, the concept. A tangent line always passes through the curve at a double or tangent point. The point where the function is neither concave nor convex is known as inflection. Point Of Inflection Has Tangent.
From www.slideserve.com
PPT 3.6 Finding the Equation of the Tangent Line to a Curve PowerPoint Presentation ID3220678 Point Of Inflection Has Tangent In this article, the concept. Inflection points and rates of change. A tangent line always passes through the curve at a double or tangent point. Let $f(x)$ be the function, $l(x)$ be the tangent at point $a$ , then passing through means $f(x). The tangent line of inflection point always passes. For all tangents to $y=x^2$, the curve lies entirely. Point Of Inflection Has Tangent.