Cycle Definition Math . in an undirected graph, a cycle has no direction associated with its edges. Cycles de nition 1.4 a cycle is a closed trail in which the \ rst vertex = last vertex is the only vertex that is repeated. A simple cycle does not repeat any vertices except. If a graph \(g\) is not. Let be the symmetric group on a set. Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the starting and ending vertex must be. Some functions (like sine and cosine) repeat forever. Cyclic chain rule, for derivatives, used in. a cycle consists of a sequence of adjacent and distinct nodes in a graph. a cycle is a type of permutation. a permutation cycle is a subset of a permutation whose elements trade places with one another. cyclic polynomials are polynomial functions that are invariant under cyclic permutation of the arguments. intuitively the surface of a torus appears to be a boundary, and so would be a cycle. amplitude, period, phase shift and frequency. A cycle is a special type of.
from learningschoolsrkagger9f.z22.web.core.windows.net
The only exception is that the first. in an undirected graph, a cycle has no direction associated with its edges. Some functions (like sine and cosine) repeat forever. intuitively the surface of a torus appears to be a boundary, and so would be a cycle. a permutation cycle is a subset of a permutation whose elements trade places with one another. A simple cycle does not repeat any vertices except. Let be the symmetric group on a set. what is cycle? a cycle in a graph is a subgraph that is a cycle. amplitude, period, phase shift and frequency.
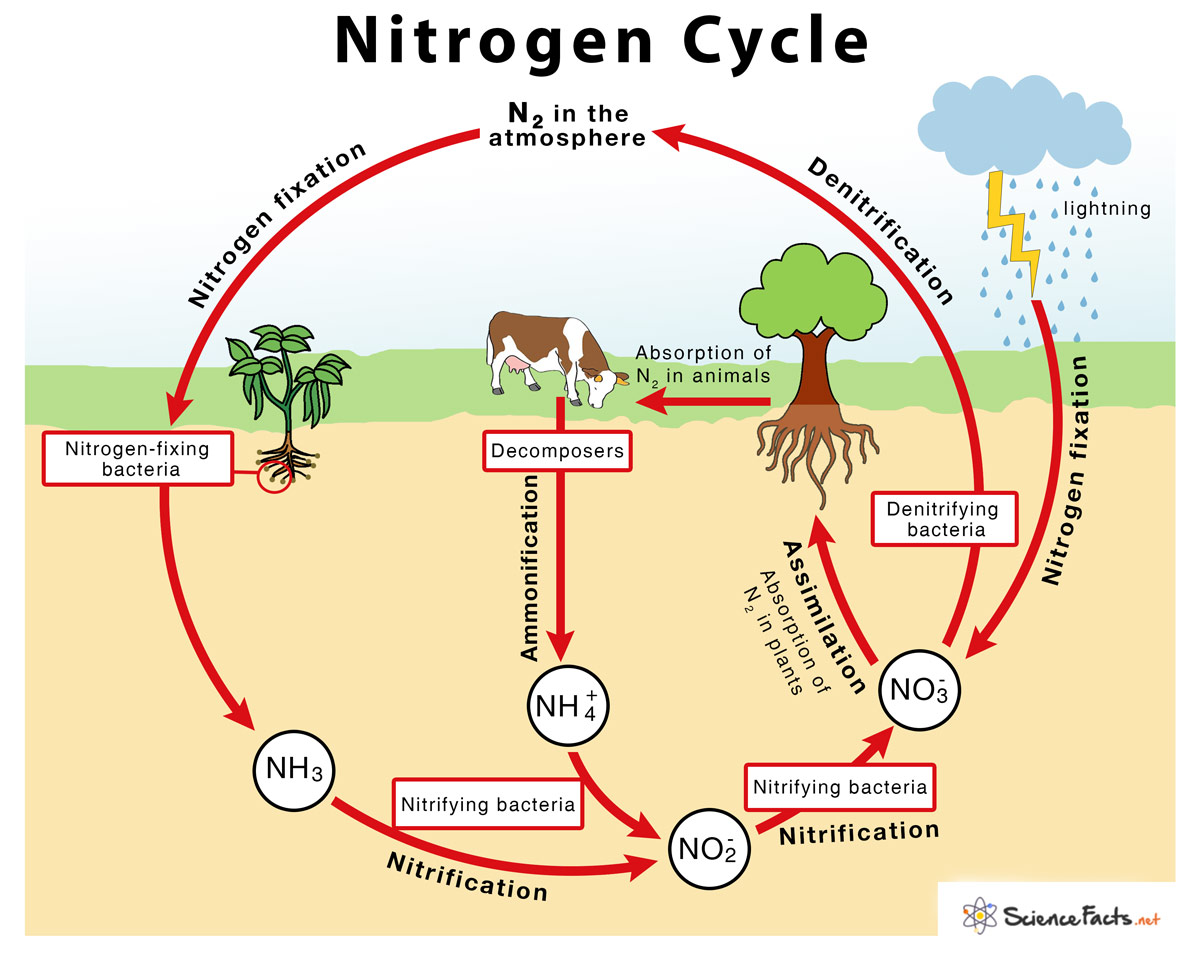
Label The Nitrogen Cycle Worksheet
Cycle Definition Math The only exception is that the first. Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the starting and ending vertex must be. The only exception is that the first. Let be an element of , and let be the subgroup of generated. a cycle in a graph is a subgraph that is a cycle. hamiltonian paths and cycles definition when g is a graph on n ≥ 3 vertices, a cycle c = (x 1, x 2,., x n) in g is called a. amplitude, period, phase shift and frequency. Some functions (like sine and cosine) repeat forever. what is cycle? If a graph \(g\) is not. in graph theory, a cycle is a path that begins and ends at the same vertex without repeating any edges or vertices, except for. intuitively the surface of a torus appears to be a boundary, and so would be a cycle. A clique in a graph is a subgraph that is a complete graph. a cycle is a type of permutation. A simple cycle does not repeat any vertices except. A cycle in graph theory is a path that starts and ends at the same vertex, visiting other vertices along the way.
From georgiasouthern.libguides.com
Research Cycle and Timeline Library Services and Resources for Cycle Definition Math Let be the symmetric group on a set. amplitude, period, phase shift and frequency. A cycle in graph theory is a path that starts and ends at the same vertex, visiting other vertices along the way. a permutation cycle is a subset of a permutation whose elements trade places with one another. what is cycle? intuitively. Cycle Definition Math.
From www.collinsdictionary.com
Cycle definition and meaning Collins English Dictionary Cycle Definition Math a cycle is a type of permutation. A simple cycle does not repeat any vertices except. Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the starting and ending vertex must be. Let be an element of , and let be the subgroup of generated. cyclic (mathematics) there are many. Cycle Definition Math.
From www.geeksforgeeks.org
Mathematics Walks, Trails, Paths, Cycles and Circuits in Graph Cycle Definition Math Let be an element of , and let be the subgroup of generated. Cycles de nition 1.4 a cycle is a closed trail in which the \ rst vertex = last vertex is the only vertex that is repeated. a permutation cycle is a subset of a permutation whose elements trade places with one another. A walk of length. Cycle Definition Math.
From learningschoolsrkagger9f.z22.web.core.windows.net
Label The Nitrogen Cycle Worksheet Cycle Definition Math cyclic polynomials are polynomial functions that are invariant under cyclic permutation of the arguments. cyclic (mathematics) there are many terms in mathematics that begin with cyclic : The only exception is that the first. a permutation of the type. Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the. Cycle Definition Math.
From www.youtube.com
What is the difference between cycle and period of a periodic function Cycle Definition Math a permutation cycle is a subset of a permutation whose elements trade places with one another. a cycle is any finite sequence of vertices $v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_n$ such that $v_i =. If a graph \(g\) is not. A walk of length at least \(1\) in which no vertex appears more than once, except that. Cycle Definition Math.
From www.youtube.com
What are Cycle Graphs? Graph Theory, Graph Cycles, Cyclic Graphs Cycle Definition Math a permutation cycle is a subset of a permutation whose elements trade places with one another. hamiltonian paths and cycles definition when g is a graph on n ≥ 3 vertices, a cycle c = (x 1, x 2,., x n) in g is called a. a cycle is any finite sequence of vertices $v_1 \rightarrow v_2. Cycle Definition Math.
From www.youtube.com
Cycle graph Types of Graph Discrete mathematics YouTube Cycle Definition Math intuitively the surface of a torus appears to be a boundary, and so would be a cycle. A cycle is a special type of. A simple cycle does not repeat any vertices except. A walk of length at least \(1\) in which no vertex appears more than once, except that the first vertex is the same as the last,. Cycle Definition Math.
From s3.amazonaws.com
L12_BipartiteMatching Cycle Definition Math Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the starting and ending vertex must be. A walk of length at least \(1\) in which no vertex appears more than once, except that the first vertex is the same as the last, is called a cycle. a cycle consists of a. Cycle Definition Math.
From www.youtube.com
Walk, Trail, Path & Circuits in graph theory with Examples YouTube Cycle Definition Math Cycles de nition 1.4 a cycle is a closed trail in which the \ rst vertex = last vertex is the only vertex that is repeated. what is cycle? A cycle is a special type of. a cycle is any finite sequence of vertices $v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_n$ such that $v_i =. A clique in. Cycle Definition Math.
From www.expii.com
Calvin Cycle (Dark Reaction) — Equation & Steps Expii Cycle Definition Math a permutation cycle is a subset of a permutation whose elements trade places with one another. in graph theory, a cycle is a path that begins and ends at the same vertex without repeating any edges or vertices, except for. a cycle is any finite sequence of vertices $v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_n$ such that. Cycle Definition Math.
From www.researchgate.net
Plot of all points collected by the force transducer and used for cycle Cycle Definition Math A simple cycle does not repeat any vertices except. Some functions (like sine and cosine) repeat forever. A walk of length at least \(1\) in which no vertex appears more than once, except that the first vertex is the same as the last, is called a cycle. in graph theory, a cycle is a path that begins and ends. Cycle Definition Math.
From www.slideserve.com
PPT What is Discrete Math? PowerPoint Presentation, free download Cycle Definition Math Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the starting and ending vertex must be. If a graph \(g\) is not. a cycle in a graph is a subgraph that is a cycle. a cycle consists of a sequence of adjacent and distinct nodes in a graph. A walk. Cycle Definition Math.
From www.slideserve.com
PPT Math 3121 Abstract Algebra I PowerPoint Presentation, free Cycle Definition Math A cycle is a special type of. amplitude, period, phase shift and frequency. intuitively the surface of a torus appears to be a boundary, and so would be a cycle. in graph theory, a cycle is a path that begins and ends at the same vertex without repeating any edges or vertices, except for. A walk of. Cycle Definition Math.
From businessyield.com
What Is BUSINESS CYCLE? Definition, Internal and External Causes Cycle Definition Math intuitively the surface of a torus appears to be a boundary, and so would be a cycle. A cycle is a special type of. Cycles de nition 1.4 a cycle is a closed trail in which the \ rst vertex = last vertex is the only vertex that is repeated. If a graph \(g\) is not. in graph. Cycle Definition Math.
From www.slideserve.com
PPT Graph Theory PowerPoint Presentation, free download ID2742356 Cycle Definition Math a permutation of the type. Some functions (like sine and cosine) repeat forever. a cycle is a type of permutation. in an undirected graph, a cycle has no direction associated with its edges. A cycle in graph theory is a path that starts and ends at the same vertex, visiting other vertices along the way. Cyclic chain. Cycle Definition Math.
From www.slideserve.com
PPT Module 19 Graph Theory part I PowerPoint Presentation, free Cycle Definition Math A cycle is a special type of. Some functions (like sine and cosine) repeat forever. Let be an element of , and let be the subgroup of generated. A clique in a graph is a subgraph that is a complete graph. in an undirected graph, a cycle has no direction associated with its edges. Let be the symmetric group. Cycle Definition Math.
From math.stackexchange.com
Number of cycles and paths in a wheel graph Mathematics Stack Exchange Cycle Definition Math If a graph \(g\) is not. Cyclic chain rule, for derivatives, used in. A cycle in graph theory is a path that starts and ends at the same vertex, visiting other vertices along the way. intuitively the surface of a torus appears to be a boundary, and so would be a cycle. A walk of length at least \(1\). Cycle Definition Math.
From www.youtube.com
Hamiltonian path Hamiltonian Circuit Hamiltonian graph with Cycle Definition Math a cycle in a graph is a subgraph that is a cycle. what is cycle? A simple cycle does not repeat any vertices except. If a graph \(g\) is not. A cycle in graph theory is a path that starts and ends at the same vertex, visiting other vertices along the way. a cycle consists of a. Cycle Definition Math.
From www.youtube.com
Spanning Tree Discrete Mathematics YouTube Cycle Definition Math a permutation cycle is a subset of a permutation whose elements trade places with one another. a cycle consists of a sequence of adjacent and distinct nodes in a graph. cyclic (mathematics) there are many terms in mathematics that begin with cyclic : Let be the symmetric group on a set. a cycle is any finite. Cycle Definition Math.
From www.researchgate.net
The mathematical cycle Download Scientific Diagram Cycle Definition Math a cycle is any finite sequence of vertices $v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_n$ such that $v_i =. hamiltonian paths and cycles definition when g is a graph on n ≥ 3 vertices, a cycle c = (x 1, x 2,., x n) in g is called a. amplitude, period, phase shift and frequency. Traversing a. Cycle Definition Math.
From www.researchgate.net
(PDF) The ProblemSolving Cycle A model of mathematics professional Cycle Definition Math a cycle in a graph is a subgraph that is a cycle. a cycle is any finite sequence of vertices $v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_n$ such that $v_i =. Let be the symmetric group on a set. what is cycle? cyclic (mathematics) there are many terms in mathematics that begin with cyclic : . Cycle Definition Math.
From www.slideserve.com
PPT BIOGEOCHEMICAL CYCLES PowerPoint Presentation ID2262441 Cycle Definition Math in an undirected graph, a cycle has no direction associated with its edges. amplitude, period, phase shift and frequency. cyclic (mathematics) there are many terms in mathematics that begin with cyclic : The only exception is that the first. a cycle consists of a sequence of adjacent and distinct nodes in a graph. hamiltonian paths. Cycle Definition Math.
From math.stackexchange.com
Define A Graph Tree Graph With "Cycles" as Nodes Mathematics Stack Cycle Definition Math A walk of length at least \(1\) in which no vertex appears more than once, except that the first vertex is the same as the last, is called a cycle. hamiltonian paths and cycles definition when g is a graph on n ≥ 3 vertices, a cycle c = (x 1, x 2,., x n) in g is called. Cycle Definition Math.
From www.youtube.com
Product of cycles example 1 YouTube Cycle Definition Math what is cycle? intuitively the surface of a torus appears to be a boundary, and so would be a cycle. Cyclic chain rule, for derivatives, used in. a cycle is any finite sequence of vertices $v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_n$ such that $v_i =. in an undirected graph, a cycle has no direction associated. Cycle Definition Math.
From timingsolution.com
Cycles apology Cycle Definition Math Let be the symmetric group on a set. A cycle is a special type of. Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the starting and ending vertex must be. Cycles de nition 1.4 a cycle is a closed trail in which the \ rst vertex = last vertex is the. Cycle Definition Math.
From www.geeksforgeeks.org
Mathematics Graph Theory Basics Set 1 Cycle Definition Math Cycles de nition 1.4 a cycle is a closed trail in which the \ rst vertex = last vertex is the only vertex that is repeated. a cycle consists of a sequence of adjacent and distinct nodes in a graph. what is cycle? A clique in a graph is a subgraph that is a complete graph. A walk. Cycle Definition Math.
From brilliant.org
Hamiltonian Path Brilliant Math & Science Wiki Cycle Definition Math hamiltonian paths and cycles definition when g is a graph on n ≥ 3 vertices, a cycle c = (x 1, x 2,., x n) in g is called a. The only exception is that the first. A cycle is a special type of. amplitude, period, phase shift and frequency. A simple cycle does not repeat any vertices. Cycle Definition Math.
From study.com
Carbon & Nitrogen Cycle Overview, Steps & Comparison Video & Lesson Cycle Definition Math Cycles de nition 1.4 a cycle is a closed trail in which the \ rst vertex = last vertex is the only vertex that is repeated. amplitude, period, phase shift and frequency. a cycle in a graph is a subgraph that is a cycle. A walk of length at least \(1\) in which no vertex appears more than. Cycle Definition Math.
From www.youtube.com
(Abstract Algebra 1) Definition of a Cyclic Group YouTube Cycle Definition Math a permutation of the type. A simple cycle does not repeat any vertices except. Cycles de nition 1.4 a cycle is a closed trail in which the \ rst vertex = last vertex is the only vertex that is repeated. in an undirected graph, a cycle has no direction associated with its edges. A walk of length at. Cycle Definition Math.
From ar.inspiredpencil.com
Define Water Cycle Cycle Definition Math A simple cycle does not repeat any vertices except. A cycle in graph theory is a path that starts and ends at the same vertex, visiting other vertices along the way. what is cycle? hamiltonian paths and cycles definition when g is a graph on n ≥ 3 vertices, a cycle c = (x 1, x 2,., x. Cycle Definition Math.
From lessondbbreakpoint.z21.web.core.windows.net
Define Euler Path And Euler Circuit Cycle Definition Math Some functions (like sine and cosine) repeat forever. A clique in a graph is a subgraph that is a complete graph. A cycle in graph theory is a path that starts and ends at the same vertex, visiting other vertices along the way. in graph theory, a cycle is a path that begins and ends at the same vertex. Cycle Definition Math.
From math.stackexchange.com
Define A Graph Tree Graph With "Cycles" as Nodes Mathematics Stack Cycle Definition Math A simple cycle does not repeat any vertices except. Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the starting and ending vertex must be. cyclic (mathematics) there are many terms in mathematics that begin with cyclic : amplitude, period, phase shift and frequency. in graph theory, a cycle. Cycle Definition Math.
From www.youtube.com
Graph Theory Walks and Paths YouTube Cycle Definition Math a cycle is any finite sequence of vertices $v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_n$ such that $v_i =. cyclic (mathematics) there are many terms in mathematics that begin with cyclic : a cycle is a type of permutation. Let be the symmetric group on a set. what is cycle? A cycle is a special type. Cycle Definition Math.
From www.picnbooks.com
Cycle definition and meaning with pictures Picture Dictionary & Books Cycle Definition Math Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the starting and ending vertex must be. a permutation cycle is a subset of a permutation whose elements trade places with one another. A cycle is a special type of. amplitude, period, phase shift and frequency. A walk of length at. Cycle Definition Math.
From www.geeksforgeeks.org
Find any simple cycle in an undirected unweighted Graph Cycle Definition Math Let be the symmetric group on a set. a cycle consists of a sequence of adjacent and distinct nodes in a graph. Traversing a graph such that we do not repeat a vertex, nor we repeat an edge but the starting and ending vertex must be. Cycles de nition 1.4 a cycle is a closed trail in which the. Cycle Definition Math.