How To Find Radius Of Circle Inscribed In Equilateral Triangle . As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20 and 24 (made up of two right angled. \(a = 2 \), \(b = 3 \), and \(c = 4 \). How to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? Find the radius \(r\) of the circumscribed circle for the triangle \(\triangle\,abc\) from example 2.6 in section 2.2: E.g if the radius was 6 and at. Incircle radius = h / 3 = a × √3 / 6. Circumcircle radius = 2 × h / 3 = a × √3 / 3. Then draw the triangle and the. R = x (x + 1) (2 x + 1). By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from the center of the equilateral triangle to any of its vertices is equal to. $a=\frac{pr}{2}$ where $p$ is the perimeter and $r$ the incircle radius. Use the fact that the area $a$ (of the triangle) is given by: Given a circle of radius $3\rm{cm}$ inscribed in an equilateral triangle $\triangle abc$ and $ezdu$ is a square inscribed in the circle. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? Find the circle's area in terms of x.
from www.geeksforgeeks.org
Use the fact that the area $a$ (of the triangle) is given by: Find the circle's area in terms of x. \(a = 2 \), \(b = 3 \), and \(c = 4 \). As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20 and 24 (made up of two right angled. Given a circle of radius $3\rm{cm}$ inscribed in an equilateral triangle $\triangle abc$ and $ezdu$ is a square inscribed in the circle. Then draw the triangle and the. This formula can easily be proved ( divide the. Incircle radius = h / 3 = a × √3 / 6. Circumcircle radius = 2 × h / 3 = a × √3 / 3. E.g if the radius was 6 and at.
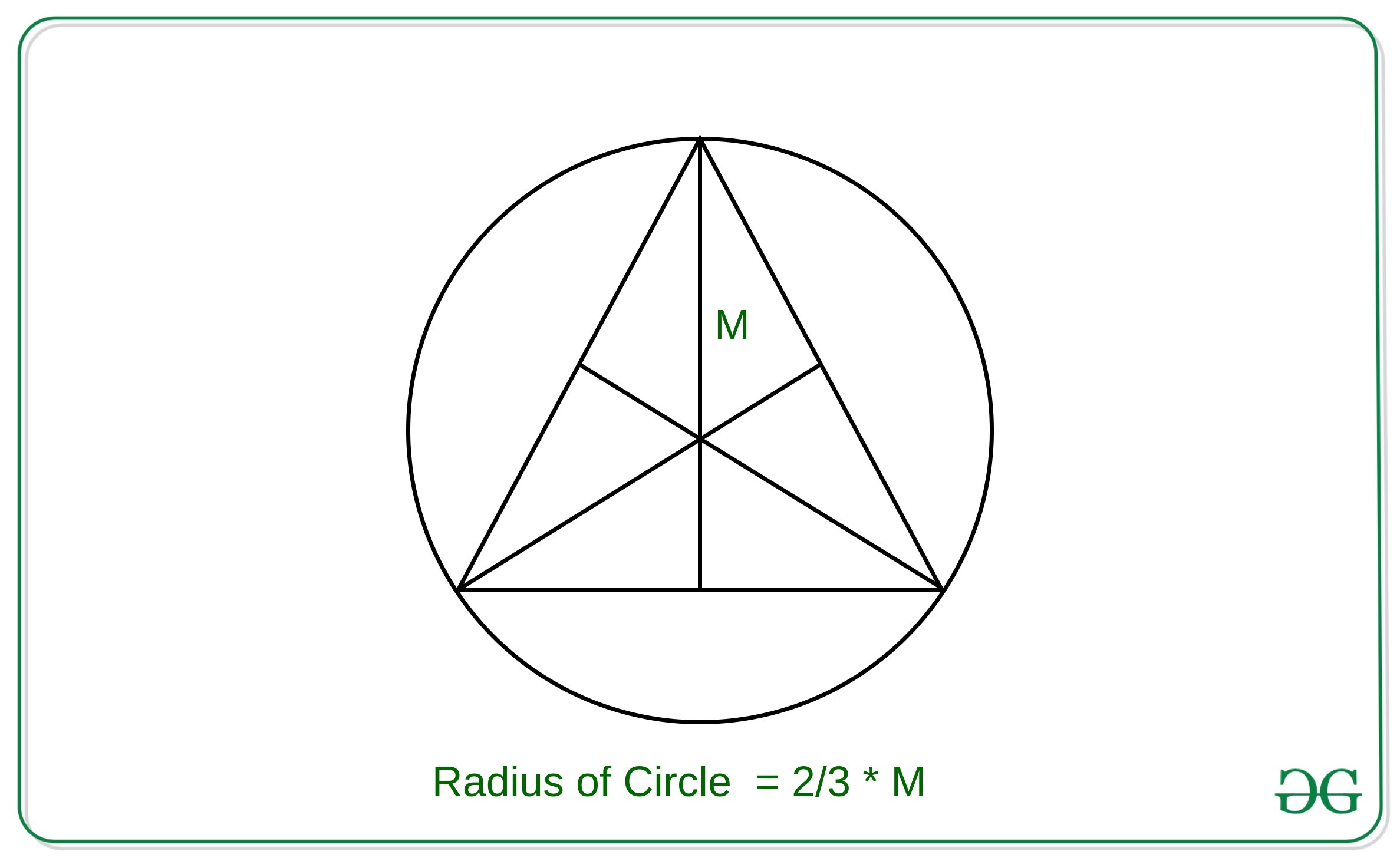
Area of Circumcircle of an Equilateral Triangle using Median
How To Find Radius Of Circle Inscribed In Equilateral Triangle Incircle radius = h / 3 = a × √3 / 6. As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20 and 24 (made up of two right angled. Circumcircle radius = 2 × h / 3 = a × √3 / 3. Given a circle of radius $3\rm{cm}$ inscribed in an equilateral triangle $\triangle abc$ and $ezdu$ is a square inscribed in the circle. Find the circle's area in terms of x. R = x (x + 1) (2 x + 1). Find the radius \(r\) of the circumscribed circle for the triangle \(\triangle\,abc\) from example 2.6 in section 2.2: This formula can easily be proved ( divide the. An equilateral triangle has side length x. E.g if the radius was 6 and at. Then draw the triangle and the. Incircle radius = h / 3 = a × √3 / 6. Use the fact that the area $a$ (of the triangle) is given by: By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from the center of the equilateral triangle to any of its vertices is equal to. How to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? \(a = 2 \), \(b = 3 \), and \(c = 4 \).
From www.toppr.com
Q21 In Fig 4, a circle is inscribed in an equilateral triangle ABC of How To Find Radius Of Circle Inscribed In Equilateral Triangle \(a = 2 \), \(b = 3 \), and \(c = 4 \). If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? How to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? Find the radius \(r\) of the circumscribed circle. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.vrogue.co
An Equilateral Triangle Abc Is Inscribed In A Circle vrogue.co How To Find Radius Of Circle Inscribed In Equilateral Triangle How to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? Find the circle's area in terms of x. An equilateral triangle has side length x. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? \(a = 2 \), \(b =. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From brainly.in
An equilateral triangle of side 9cm is inscribed in a circle. Find its How To Find Radius Of Circle Inscribed In Equilateral Triangle This formula can easily be proved ( divide the. \(a = 2 \), \(b = 3 \), and \(c = 4 \). Given a circle of radius $3\rm{cm}$ inscribed in an equilateral triangle $\triangle abc$ and $ezdu$ is a square inscribed in the circle. By symmetry, the center of the equilateral triangle coincides with the center of the circle, and. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From ar.inspiredpencil.com
Circumscribed Equilateral Triangle How To Find Radius Of Circle Inscribed In Equilateral Triangle Find the radius \(r\) of the circumscribed circle for the triangle \(\triangle\,abc\) from example 2.6 in section 2.2: Find the circle's area in terms of x. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? As an example, for x=1, m=4, n=2, the isosceles triangle has sides. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From byjus.com
Consider an equilateral triangle in which the length of one side is 6 How To Find Radius Of Circle Inscribed In Equilateral Triangle E.g if the radius was 6 and at. Given a circle of radius $3\rm{cm}$ inscribed in an equilateral triangle $\triangle abc$ and $ezdu$ is a square inscribed in the circle. By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from the center of the equilateral triangle to any of its vertices. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.traingleworksheets.com
Equilateral Triangle In A Circle How To Find Radius Of Circle Inscribed In Equilateral Triangle E.g if the radius was 6 and at. By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from the center of the equilateral triangle to any of its vertices is equal to. As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20 and 24 (made. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.youtube.com
HOW TO INSCRIBE AN EQUILATERAL TRIANGLE IN A CIRCLE Draw an How To Find Radius Of Circle Inscribed In Equilateral Triangle An equilateral triangle has side length x. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? Find the circle's area in terms of x. Use the fact that the area $a$ (of the triangle) is given by: Circumcircle radius = 2 × h / 3 = a. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.quora.com
How to find the length of one side of an equilateral triangle that is How To Find Radius Of Circle Inscribed In Equilateral Triangle How to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? Circumcircle radius = 2 × h / 3 = a × √3 / 3. Incircle radius = h / 3 = a × √3 / 6. Then draw the triangle and the. An equilateral triangle has side length x. $a=\frac{pr}{2}$ where $p$ is. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.geeksforgeeks.org
Area of Circumcircle of an Equilateral Triangle using Median How To Find Radius Of Circle Inscribed In Equilateral Triangle $a=\frac{pr}{2}$ where $p$ is the perimeter and $r$ the incircle radius. How to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? \(a = 2 \), \(b = 3 \), and \(c = 4 \). By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.youtube.com
Finding the Radius of an Inscribed Circle in a Triangle YouTube How To Find Radius Of Circle Inscribed In Equilateral Triangle \(a = 2 \), \(b = 3 \), and \(c = 4 \). If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? Find the radius \(r\) of the circumscribed circle for the triangle \(\triangle\,abc\) from example 2.6 in section 2.2: Find the circle's area in terms of. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From ar.inspiredpencil.com
Inscribed Triangle How To Find Radius Of Circle Inscribed In Equilateral Triangle Then draw the triangle and the. E.g if the radius was 6 and at. Find the radius \(r\) of the circumscribed circle for the triangle \(\triangle\,abc\) from example 2.6 in section 2.2: Incircle radius = h / 3 = a × √3 / 6. As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.meritnation.com
ABC is an equilateral triangle inscribed in a circle of radius 4cm find How To Find Radius Of Circle Inscribed In Equilateral Triangle As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20 and 24 (made up of two right angled. Find the circle's area in terms of x. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? Circumcircle radius = 2 × h. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.vedantu.com
An equilateral triangle of side 9 cm is inscribed in a circle. Find How To Find Radius Of Circle Inscribed In Equilateral Triangle E.g if the radius was 6 and at. Find the circle's area in terms of x. Find the radius \(r\) of the circumscribed circle for the triangle \(\triangle\,abc\) from example 2.6 in section 2.2: If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? $a=\frac{pr}{2}$ where $p$ is. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From campolden.org
How To Make An Equilateral Triangle Inscribed In A Circle Templates How To Find Radius Of Circle Inscribed In Equilateral Triangle This formula can easily be proved ( divide the. How to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? Then draw the triangle and the. E.g if the radius was 6 and at. Use the fact that the area $a$ (of the triangle) is given by: Find the circle's area in terms of. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.toppr.com
An equilateral triangle of side 9 cm is inscribed in a circle. Find the How To Find Radius Of Circle Inscribed In Equilateral Triangle \(a = 2 \), \(b = 3 \), and \(c = 4 \). Then draw the triangle and the. R = x (x + 1) (2 x + 1). As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20 and 24 (made up of two right angled. By symmetry, the center of the equilateral. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.alamy.com
An illustration showing how to construct an equilateral triangle How To Find Radius Of Circle Inscribed In Equilateral Triangle This formula can easily be proved ( divide the. An equilateral triangle has side length x. By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from the center of the equilateral triangle to any of its vertices is equal to. Then draw the triangle and the. Find the circle's area in. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.meritnation.com
In the given figure,PQR is an equilateral triangle inscribed in a How To Find Radius Of Circle Inscribed In Equilateral Triangle R = x (x + 1) (2 x + 1). An equilateral triangle has side length x. E.g if the radius was 6 and at. \(a = 2 \), \(b = 3 \), and \(c = 4 \). Find the radius \(r\) of the circumscribed circle for the triangle \(\triangle\,abc\) from example 2.6 in section 2.2: Then draw the triangle. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From byjus.com
An equilateral triangle ABC is inscribed in a circle of radius 12 cm How To Find Radius Of Circle Inscribed In Equilateral Triangle If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? R = x (x + 1) (2 x + 1). This formula can easily be proved ( divide the. Circumcircle radius = 2 × h / 3 = a × √3 / 3. By symmetry, the center of. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.doubtnut.com
ABC is an equilateral triangle inscribed in a circle of radius 4 cm. F How To Find Radius Of Circle Inscribed In Equilateral Triangle E.g if the radius was 6 and at. Use the fact that the area $a$ (of the triangle) is given by: \(a = 2 \), \(b = 3 \), and \(c = 4 \). An equilateral triangle has side length x. How to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? Given a. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From byjus.com
An equilateral triangle of side 9 cm is inscribed in a circle then the How To Find Radius Of Circle Inscribed In Equilateral Triangle $a=\frac{pr}{2}$ where $p$ is the perimeter and $r$ the incircle radius. As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20 and 24 (made up of two right angled. Find the circle's area in terms of x. E.g if the radius was 6 and at. This formula can easily be proved ( divide the.. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.geeksforgeeks.org
Area of Equilateral triangle inscribed in a Circle of radius R How To Find Radius Of Circle Inscribed In Equilateral Triangle Then draw the triangle and the. Circumcircle radius = 2 × h / 3 = a × √3 / 3. Find the radius \(r\) of the circumscribed circle for the triangle \(\triangle\,abc\) from example 2.6 in section 2.2: Use the fact that the area $a$ (of the triangle) is given by: As an example, for x=1, m=4, n=2, the isosceles. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From brainly.in
The radius of a circle inscribed in an equilateral triangle is 10 cm How To Find Radius Of Circle Inscribed In Equilateral Triangle Circumcircle radius = 2 × h / 3 = a × √3 / 3. Use the fact that the area $a$ (of the triangle) is given by: As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20 and 24 (made up of two right angled. Find the radius \(r\) of the circumscribed circle for. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From mathcountsnotes.blogspot.com
mathcounts notes 2014 Mathcounts State Prep Inscribed Circle Radius How To Find Radius Of Circle Inscribed In Equilateral Triangle Then draw the triangle and the. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? $a=\frac{pr}{2}$ where $p$ is the perimeter and $r$ the incircle radius. R = x (x + 1) (2 x + 1). As an example, for x=1, m=4, n=2, the isosceles triangle has. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From atlanticgmat.com
In the figure above, equilateral triangle ABC is inscribed in the How To Find Radius Of Circle Inscribed In Equilateral Triangle By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from the center of the equilateral triangle to any of its vertices is equal to. $a=\frac{pr}{2}$ where $p$ is the perimeter and $r$ the incircle radius. E.g if the radius was 6 and at. This formula can easily be proved ( divide. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.youtube.com
An Equilateral Triangle of Side 9cm is Inscribed in a Circle. Find the How To Find Radius Of Circle Inscribed In Equilateral Triangle Then draw the triangle and the. Use the fact that the area $a$ (of the triangle) is given by: Find the radius \(r\) of the circumscribed circle for the triangle \(\triangle\,abc\) from example 2.6 in section 2.2: Circumcircle radius = 2 × h / 3 = a × √3 / 3. E.g if the radius was 6 and at. \(a. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From mathibayon.blogspot.com
Derivation of Formula for the Radius of Circumcircle MATHibayon How To Find Radius Of Circle Inscribed In Equilateral Triangle This formula can easily be proved ( divide the. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? How to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? \(a = 2 \), \(b = 3 \), and \(c = 4. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.youtube.com
Radius of the incircle of an Equilateral Triangle YouTube How To Find Radius Of Circle Inscribed In Equilateral Triangle \(a = 2 \), \(b = 3 \), and \(c = 4 \). $a=\frac{pr}{2}$ where $p$ is the perimeter and $r$ the incircle radius. By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from the center of the equilateral triangle to any of its vertices is equal to. Given a circle. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From byjus.com
if an equilateral triangle is inscribed in a circle of radius 10 cm How To Find Radius Of Circle Inscribed In Equilateral Triangle By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from the center of the equilateral triangle to any of its vertices is equal to. Incircle radius = h / 3 = a × √3 / 6. This formula can easily be proved ( divide the. Circumcircle radius = 2 × h. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.coursehero.com
[Solved] An equilateral triangle is inscribed in a circle of radius 2r How To Find Radius Of Circle Inscribed In Equilateral Triangle If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? Use the fact that the area $a$ (of the triangle) is given by: Then draw the triangle and the. R = x (x + 1) (2 x + 1). How to find the radius of the circle circumscribing. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.youtube.com
Formula to find the radius of an inscribed circle of a triangle How To Find Radius Of Circle Inscribed In Equilateral Triangle E.g if the radius was 6 and at. \(a = 2 \), \(b = 3 \), and \(c = 4 \). By symmetry, the center of the equilateral triangle coincides with the center of the circle, and the distance from the center of the equilateral triangle to any of its vertices is equal to. Given a circle of radius $3\rm{cm}$. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.youtube.com
An equilateral triangle of side 9cm inscribed in a circle The radius of How To Find Radius Of Circle Inscribed In Equilateral Triangle Find the circle's area in terms of x. E.g if the radius was 6 and at. \(a = 2 \), \(b = 3 \), and \(c = 4 \). Circumcircle radius = 2 × h / 3 = a × √3 / 3. If there is an equilateral triangle in a circle, would the midpoint of any of the 3. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From byjus.com
35. Find the side of an equilateral triangle inscribed in a circle of How To Find Radius Of Circle Inscribed In Equilateral Triangle Circumcircle radius = 2 × h / 3 = a × √3 / 3. R = x (x + 1) (2 x + 1). If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? \(a = 2 \), \(b = 3 \), and \(c = 4 \). $a=\frac{pr}{2}$. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From mathibayon.blogspot.com
Derivation of Formula for the Radius of Incircle MATHibayon How To Find Radius Of Circle Inscribed In Equilateral Triangle Circumcircle radius = 2 × h / 3 = a × √3 / 3. $a=\frac{pr}{2}$ where $p$ is the perimeter and $r$ the incircle radius. Find the circle's area in terms of x. Use the fact that the area $a$ (of the triangle) is given by: R = x (x + 1) (2 x + 1). As an example, for. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.doubtnut.com
A circle is inscribed in an equilateral triangle of side a. Find the How To Find Radius Of Circle Inscribed In Equilateral Triangle If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? An equilateral triangle has side length x. \(a = 2 \), \(b = 3 \), and \(c = 4 \). Use the fact that the area $a$ (of the triangle) is given by: Find the circle's area in. How To Find Radius Of Circle Inscribed In Equilateral Triangle.
From www.youtube.com
Equilateral Triangle Area from Incircle Radius YouTube How To Find Radius Of Circle Inscribed In Equilateral Triangle Use the fact that the area $a$ (of the triangle) is given by: \(a = 2 \), \(b = 3 \), and \(c = 4 \). Find the circle's area in terms of x. E.g if the radius was 6 and at. Given a circle of radius $3\rm{cm}$ inscribed in an equilateral triangle $\triangle abc$ and $ezdu$ is a square. How To Find Radius Of Circle Inscribed In Equilateral Triangle.