Triangles To Theorem . Sum of the measures of two angles = 75° + 60° = 135°. Using the properties of a triangle, we know that the sum of all three angles of triangle =. Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less. The hypotenuse is the largest side in a right triangle and is always opposite the right angle. The theorem about unequal pairs, though, goes a little farther. Given unequal angles, the theorem holds that the longer side of the triangle will. A 2 + b 2 = c 2. (only right triangles have a hypotenuse). Identify the legs and the hypotenuse of the right triangle. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. It is called pythagoras' theorem and can be written in one short equation: C is the longest side of the triangle; The legs have length 24 and x.
from mathmonks.com
(only right triangles have a hypotenuse). The theorem about unequal pairs, though, goes a little farther. The hypotenuse is the largest side in a right triangle and is always opposite the right angle. A 2 + b 2 = c 2. Identify the legs and the hypotenuse of the right triangle. Sum of the measures of two angles = 75° + 60° = 135°. Given unequal angles, the theorem holds that the longer side of the triangle will. It is called pythagoras' theorem and can be written in one short equation: C is the longest side of the triangle; The legs have length 24 and x.
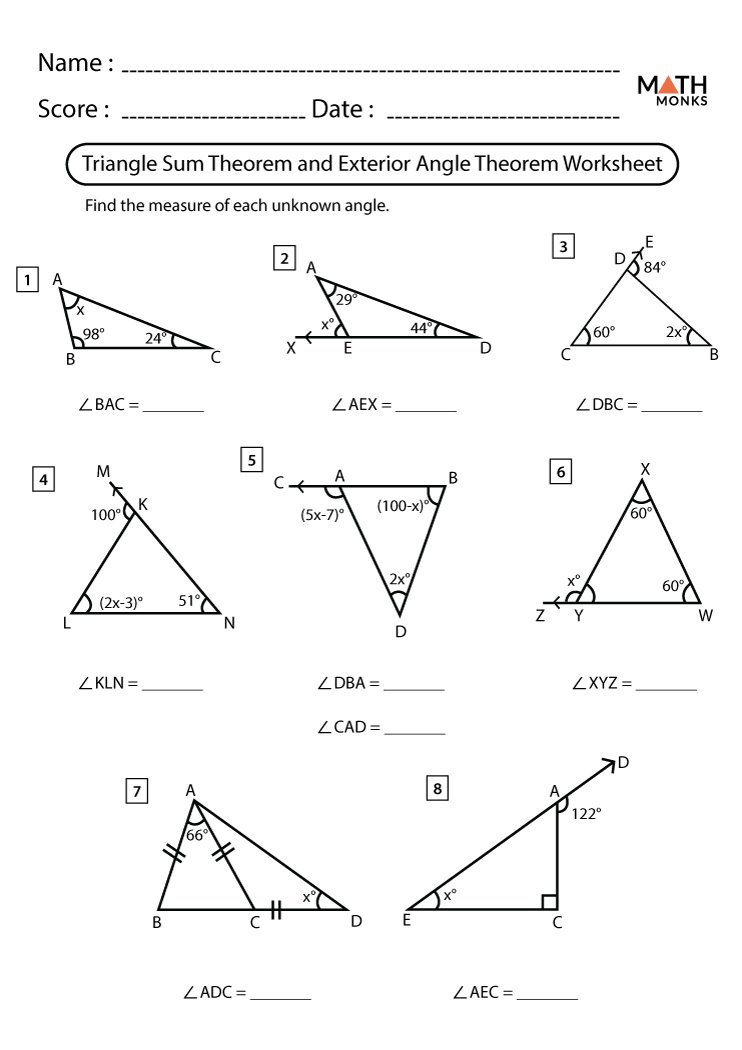
Triangle Sum Theorem Worksheets Math Monks
Triangles To Theorem Sum of the measures of two angles = 75° + 60° = 135°. Identify the legs and the hypotenuse of the right triangle. The theorem about unequal pairs, though, goes a little farther. Sum of the measures of two angles = 75° + 60° = 135°. Using the properties of a triangle, we know that the sum of all three angles of triangle =. (only right triangles have a hypotenuse). The legs have length 24 and x. A 2 + b 2 = c 2. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. Given unequal angles, the theorem holds that the longer side of the triangle will. Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less. The hypotenuse is the largest side in a right triangle and is always opposite the right angle. It is called pythagoras' theorem and can be written in one short equation: C is the longest side of the triangle;
From cookinglove.com
List of triangle theorems Triangles To Theorem Given unequal angles, the theorem holds that the longer side of the triangle will. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. Using the properties of a triangle, we know that the sum of all three angles of triangle =. The theorem about unequal pairs, though, goes a little farther. Three examples. Triangles To Theorem.
From www.teachoo.com
Theorem 6.8 Pythagoras Theorem Proof Class 10 Chapter 6 Triangles To Theorem The theorem about unequal pairs, though, goes a little farther. Identify the legs and the hypotenuse of the right triangle. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. C is the longest side of the triangle; The legs have length 24 and x. (only right triangles have a hypotenuse). Three examples of. Triangles To Theorem.
From healthy-food-near-me.com
Pythagorean theorem for a right triangle formula and problems Triangles To Theorem Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less. C is the longest side of the triangle; Sum of the measures of two angles = 75° + 60° = 135°. The hypotenuse is the largest side in a right triangle and is always opposite. Triangles To Theorem.
From www.varsitytutors.com
Prove theorems about triangles. Common Core High School Geometry Triangles To Theorem Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. C is the longest side of the triangle; Given unequal angles, the theorem holds that the longer side of the triangle will. The theorem about unequal pairs, though, goes a little farther. (only right triangles have a hypotenuse). Identify the legs and the hypotenuse. Triangles To Theorem.
From www.madebyteachers.com
Triangle Angle Theorems Digital Activity Drag & Drop Made By Teachers Triangles To Theorem Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. The theorem about unequal pairs, though, goes a little farther. Identify the legs and the hypotenuse of the right. Triangles To Theorem.
From mathmonks.com
Triangle Inequality Theorem Worksheets Math Monks Triangles To Theorem Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. Sum of the measures of two angles = 75° + 60° = 135°. Given unequal angles, the theorem holds that the longer side of the triangle will. A 2 + b 2 = c 2. The theorem about unequal pairs, though, goes a little. Triangles To Theorem.
From owlcation.com
Triangle Proportionality Theorem (With Proof and Examples) Owlcation Triangles To Theorem The hypotenuse is the largest side in a right triangle and is always opposite the right angle. The legs have length 24 and x. Identify the legs and the hypotenuse of the right triangle. Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less. Using. Triangles To Theorem.
From www.teachoo.com
Theorem 6.3 (AAA Similarity) Class 10 If corresponding angles equal Triangles To Theorem C is the longest side of the triangle; Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less. Using the properties of a triangle, we know that the sum of all three angles of triangle =. The legs have length 24 and x. Identify the. Triangles To Theorem.
From djstereo77.blogspot.com
Triangle Sum Theorem Worksheet DJSTEREO77 Triangles To Theorem Using the properties of a triangle, we know that the sum of all three angles of triangle =. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. Sum of the measures of two angles = 75° + 60° = 135°. The legs have length 24 and x. A 2 + b 2 =. Triangles To Theorem.
From www.teachoo.com
Theorem 6.6 Class 10 Prove that Ratio of Areas of 2 Similar Triangle Triangles To Theorem (only right triangles have a hypotenuse). A 2 + b 2 = c 2. Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less. It is called pythagoras' theorem and can be written in one short equation: The hypotenuse is the largest side in a. Triangles To Theorem.
From www.gauthmath.com
Solved 3. Match the similar triangles to the postulate or theorem that Triangles To Theorem The hypotenuse is the largest side in a right triangle and is always opposite the right angle. Given unequal angles, the theorem holds that the longer side of the triangle will. (only right triangles have a hypotenuse). Sum of the measures of two angles = 75° + 60° = 135°. Using the properties of a triangle, we know that the. Triangles To Theorem.
From thelmaphoto7.blogspot.com
Geometry Theorems Cheat Sheet / Geometry Cheat Sheet Theorems Formulas Triangles To Theorem Using the properties of a triangle, we know that the sum of all three angles of triangle =. (only right triangles have a hypotenuse). A 2 + b 2 = c 2. Sum of the measures of two angles = 75° + 60° = 135°. Given unequal angles, the theorem holds that the longer side of the triangle will. Three. Triangles To Theorem.
From www.toppr.com
Similarity of Triangles Types, Properties, Theorems with Videos, Examples Triangles To Theorem The hypotenuse is the largest side in a right triangle and is always opposite the right angle. Given unequal angles, the theorem holds that the longer side of the triangle will. A 2 + b 2 = c 2. The theorem about unequal pairs, though, goes a little farther. (only right triangles have a hypotenuse). Example 2 (solving for a. Triangles To Theorem.
From www.cuemath.com
Similar Triangles Formulas, Properties, Theorems, Proofs Triangles To Theorem Given unequal angles, the theorem holds that the longer side of the triangle will. The legs have length 24 and x. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. The theorem about unequal pairs, though, goes a little farther. Three examples of the triangle inequality for triangles with sides of lengths x,. Triangles To Theorem.
From andymath.com
Triangle Inequality Theorem Triangles To Theorem The hypotenuse is the largest side in a right triangle and is always opposite the right angle. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. (only right triangles have a hypotenuse). C is the longest side of the triangle; Using the properties of a triangle, we know that the sum of all. Triangles To Theorem.
From www.traingleworksheets.com
Triangle Sum Theorem Worksheet Triangles To Theorem Using the properties of a triangle, we know that the sum of all three angles of triangle =. (only right triangles have a hypotenuse). Identify the legs and the hypotenuse of the right triangle. Sum of the measures of two angles = 75° + 60° = 135°. Example 2 (solving for a leg) use the pythagorean theorem to determine the. Triangles To Theorem.
From www.teachoo.com
Theorem 6.3 (AAA Similarity) Class 10 If corresponding angles equal Triangles To Theorem The theorem about unequal pairs, though, goes a little farther. Given unequal angles, the theorem holds that the longer side of the triangle will. It is called pythagoras' theorem and can be written in one short equation: The hypotenuse is the largest side in a right triangle and is always opposite the right angle. The legs have length 24 and. Triangles To Theorem.
From www.teachoo.com
Theorem 6.8 (Pythagoras Theorem) Class 10 Chapter 6 Triangles Theo Triangles To Theorem Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less. Identify the legs and the hypotenuse of the right triangle. A 2 + b 2 = c 2. (only right triangles have a hypotenuse). It is called pythagoras' theorem and can be written in one. Triangles To Theorem.
From studylib.net
List of common Triangle Theorems you can use when proving other Triangles To Theorem The legs have length 24 and x. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. C is the longest side of the triangle; Identify the legs and the hypotenuse of the right triangle. The hypotenuse is the largest side in a right triangle and is always opposite the right angle. A 2. Triangles To Theorem.
From mathmonks.com
Triangle Sum Theorem Worksheets Math Monks Triangles To Theorem A 2 + b 2 = c 2. (only right triangles have a hypotenuse). Sum of the measures of two angles = 75° + 60° = 135°. Given unequal angles, the theorem holds that the longer side of the triangle will. The theorem about unequal pairs, though, goes a little farther. The hypotenuse is the largest side in a right. Triangles To Theorem.
From mathmonks.com
Congruent Triangles Worksheets Math Monks Triangles To Theorem Using the properties of a triangle, we know that the sum of all three angles of triangle =. Identify the legs and the hypotenuse of the right triangle. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. C is the longest side of the triangle; The theorem about unequal pairs, though, goes a. Triangles To Theorem.
From davida.davivienda.com
Triangle Proportionality Theorem Worksheet Answer Key Printable Word Triangles To Theorem The hypotenuse is the largest side in a right triangle and is always opposite the right angle. The theorem about unequal pairs, though, goes a little farther. C is the longest side of the triangle; Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. (only right triangles have a hypotenuse). Using the properties. Triangles To Theorem.
From www.teachoo.com
Theorem 6.1 Basic Proportionality Theorem (BPT) Chapter 6 Class 10 Triangles To Theorem Using the properties of a triangle, we know that the sum of all three angles of triangle =. A 2 + b 2 = c 2. (only right triangles have a hypotenuse). Given unequal angles, the theorem holds that the longer side of the triangle will. The legs have length 24 and x. It is called pythagoras' theorem and can. Triangles To Theorem.
From bradleynewslewis.blogspot.com
9 Most Common Properties Definitions and Theorems for Triangles Triangles To Theorem Sum of the measures of two angles = 75° + 60° = 135°. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. Identify the legs and the hypotenuse of the right triangle. (only right triangles have a hypotenuse). Given unequal angles, the theorem holds that the longer side of the triangle will. Three. Triangles To Theorem.
From www.media4math.com
Student Tutorial Triangle Theorems Media4Math Triangles To Theorem The theorem about unequal pairs, though, goes a little farther. The legs have length 24 and x. Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less. The hypotenuse is the largest side in a right triangle and is always opposite the right angle. Given. Triangles To Theorem.
From www.slideserve.com
PPT Lesson 8.4 & 8.5 Similar Triangles PowerPoint Presentation ID Triangles To Theorem Sum of the measures of two angles = 75° + 60° = 135°. The hypotenuse is the largest side in a right triangle and is always opposite the right angle. Using the properties of a triangle, we know that the sum of all three angles of triangle =. C is the longest side of the triangle; The theorem about unequal. Triangles To Theorem.
From mathmonks.com
Triangle Sum Theorem Worksheets Math Monks Triangles To Theorem Using the properties of a triangle, we know that the sum of all three angles of triangle =. The legs have length 24 and x. C is the longest side of the triangle; Given unequal angles, the theorem holds that the longer side of the triangle will. The theorem about unequal pairs, though, goes a little farther. A 2 +. Triangles To Theorem.
From www.media4math.com
Student Tutorial Triangle Theorems Media4Math Triangles To Theorem The hypotenuse is the largest side in a right triangle and is always opposite the right angle. Using the properties of a triangle, we know that the sum of all three angles of triangle =. A 2 + b 2 = c 2. It is called pythagoras' theorem and can be written in one short equation: (only right triangles have. Triangles To Theorem.
From www.teachoo.com
Theorem 6.6 Class 10 Prove that Ratio of Areas of 2 Similar Triangle Triangles To Theorem Using the properties of a triangle, we know that the sum of all three angles of triangle =. A 2 + b 2 = c 2. Sum of the measures of two angles = 75° + 60° = 135°. C is the longest side of the triangle; Three examples of the triangle inequality for triangles with sides of lengths x,. Triangles To Theorem.
From www.teachoo.com
Theorem 6.6 Class 10 Prove that Ratio of Areas of 2 Similar Triangle Triangles To Theorem Identify the legs and the hypotenuse of the right triangle. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. A 2 + b 2 = c 2. Sum of the measures of two angles = 75° + 60° = 135°. The legs have length 24 and x. (only right triangles have a hypotenuse).. Triangles To Theorem.
From mytutorsource.hk
How to Prove Similar Triangles Similarity Theorems Triangles To Theorem C is the longest side of the triangle; Given unequal angles, the theorem holds that the longer side of the triangle will. Using the properties of a triangle, we know that the sum of all three angles of triangle =. Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. The hypotenuse is the. Triangles To Theorem.
From www.teachoo.com
Theorem 6.5 (SAS Similarity) If one angle of a triangle is equal to Triangles To Theorem Given unequal angles, the theorem holds that the longer side of the triangle will. Sum of the measures of two angles = 75° + 60° = 135°. The hypotenuse is the largest side in a right triangle and is always opposite the right angle. C is the longest side of the triangle; A 2 + b 2 = c 2.. Triangles To Theorem.
From www.madebyteachers.com
Triangle Angle Theorems Digital Activity Drag & Drop Made By Teachers Triangles To Theorem The legs have length 24 and x. Identify the legs and the hypotenuse of the right triangle. A 2 + b 2 = c 2. The theorem about unequal pairs, though, goes a little farther. Three examples of the triangle inequality for triangles with sides of lengths x, y, z.the top example shows a case where z is much less.. Triangles To Theorem.
From www.teachoo.com
Theorem 6.5 (SAS Similarity) If one angle of a triangle is equal to Triangles To Theorem The hypotenuse is the largest side in a right triangle and is always opposite the right angle. A 2 + b 2 = c 2. The legs have length 24 and x. C is the longest side of the triangle; It is called pythagoras' theorem and can be written in one short equation: The theorem about unequal pairs, though, goes. Triangles To Theorem.
From blogmath123.wordpress.com
Geometry Formulas Triangles Blog Math 123 Triangles To Theorem Example 2 (solving for a leg) use the pythagorean theorem to determine the length of x. Given unequal angles, the theorem holds that the longer side of the triangle will. It is called pythagoras' theorem and can be written in one short equation: The hypotenuse is the largest side in a right triangle and is always opposite the right angle.. Triangles To Theorem.