Unit Disc Equation . First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. In general, a dirichlet problem in a region \(a\) asks you to solve a. Harmonic functions on the unit disk. A closed unit disc is the set of points whose distance from p p is less than or equal to one: One attractive feature of the circle $|z|=1$ is that. When you mention the laplace equation, you probably have the disk in mind. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. Unit discs are a special case of unit ball.
from www.adda247.com
Harmonic functions on the unit disk. One attractive feature of the circle $|z|=1$ is that. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. Unit discs are a special case of unit ball. In general, a dirichlet problem in a region \(a\) asks you to solve a. We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. When you mention the laplace equation, you probably have the disk in mind. A closed unit disc is the set of points whose distance from p p is less than or equal to one:
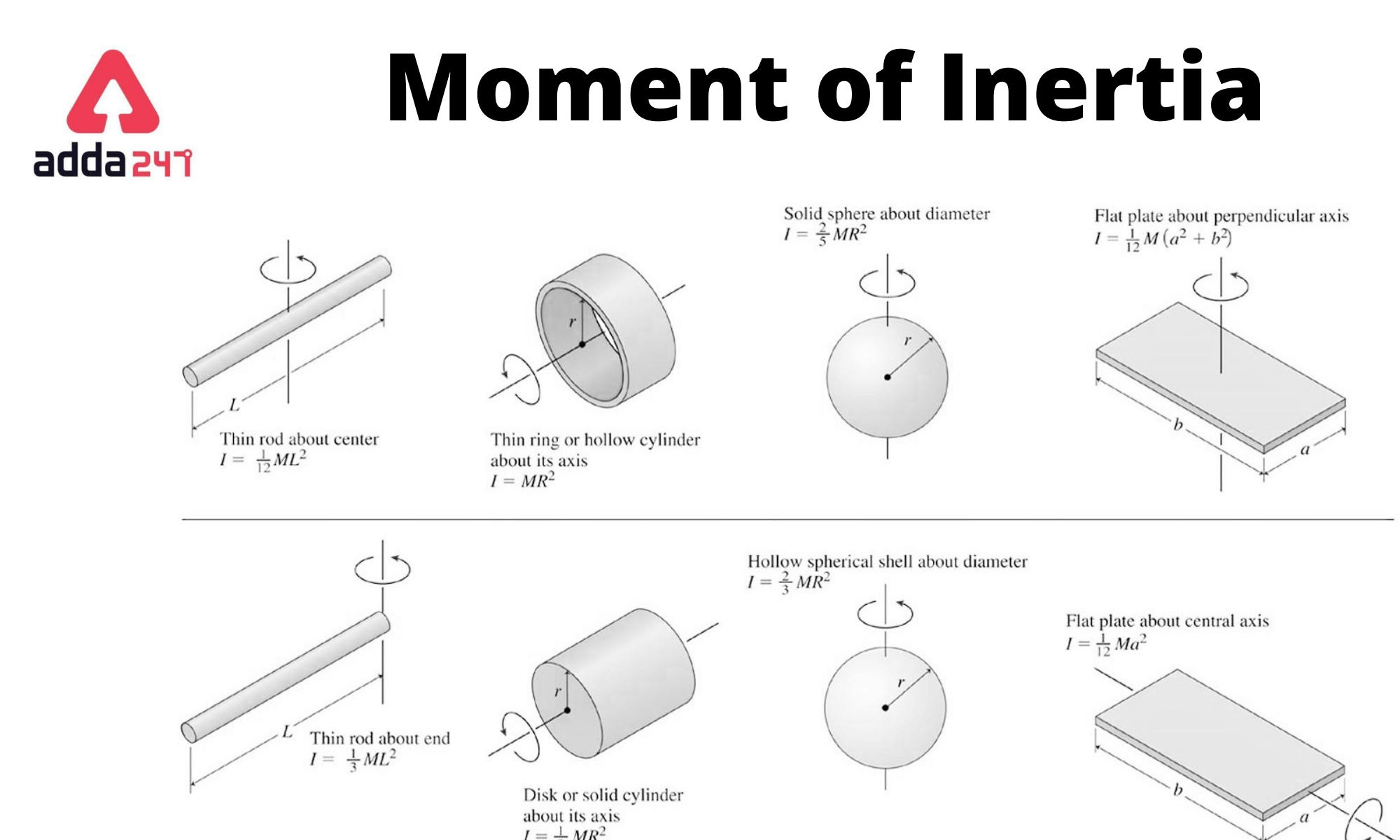
Moment of Inertia Definition, Formula, Examples, Unit, Equations
Unit Disc Equation Unit discs are a special case of unit ball. In general, a dirichlet problem in a region \(a\) asks you to solve a. A closed unit disc is the set of points whose distance from p p is less than or equal to one: We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. Harmonic functions on the unit disk. Unit discs are a special case of unit ball. One attractive feature of the circle $|z|=1$ is that. When you mention the laplace equation, you probably have the disk in mind. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values.
From la.mathworks.com
Solve Poisson Equation on Unit Disk Using PhysicsInformed Neural Unit Disc Equation First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. A closed unit disc is the set of points whose distance from p p is less than or equal to one: We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for. Unit Disc Equation.
From www.researchgate.net
(PDF) Evolution Families and the Loewner Equation I The Unit Disc Unit Disc Equation One attractive feature of the circle $|z|=1$ is that. We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. Harmonic functions on the unit disk. Unit discs are a special case of unit ball. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in. Unit Disc Equation.
From www.mathworks.com
Poisson's Equation on Unit Disk PDE Modeler App MATLAB & Simulink Unit Disc Equation Harmonic functions on the unit disk. When you mention the laplace equation, you probably have the disk in mind. We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. The poisson formula enables us to solve the boundary value problem 2 = 0 in the. Unit Disc Equation.
From www.researchgate.net
(PDF) Growth of Solutions of Higher Order Complex Linear Differential Unit Disc Equation We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. One attractive feature of the circle $|z|=1$ is that. A closed unit disc is the set. Unit Disc Equation.
From www.researchgate.net
(PDF) The wave equation of fractional order in the unit disk Unit Disc Equation Harmonic functions on the unit disk. In general, a dirichlet problem in a region \(a\) asks you to solve a. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values.. Unit Disc Equation.
From www.mathworks.com
Poisson's Equation on Unit Disk PDE Modeler App MATLAB & Simulink Unit Disc Equation The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. A closed unit disc is the set of points whose distance from p p is less than or equal to one: First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u}. Unit Disc Equation.
From www.researchgate.net
(PDF) [p, q]order of solutions of complex differential equations in a Unit Disc Equation Unit discs are a special case of unit ball. One attractive feature of the circle $|z|=1$ is that. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it. Unit Disc Equation.
From byjus.com
Moment Of Inertia Formula, Unit, Dimension And Solved Examples Unit Disc Equation Unit discs are a special case of unit ball. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. Harmonic functions on the unit disk. One attractive feature of the circle $|z|=1$ is that. In general, a dirichlet problem in a region \(a\) asks you to solve a. When. Unit Disc Equation.
From www.numerade.com
SOLVED What is different when solving the Laplace equation outside the Unit Disc Equation We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. One attractive feature of the circle $|z|=1$ is that. Harmonic functions on the unit disk. In general, a dirichlet problem in a region \(a\) asks you to solve a. When you mention the laplace equation,. Unit Disc Equation.
From www.researchgate.net
2 The feasible region R is the open unit disk. The region W is the Unit Disc Equation The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. In general, a dirichlet problem in a region \(a\) asks you to solve a.. Unit Disc Equation.
From www.researchgate.net
Laplace Equation 17 in the unit disk. Solutions on the inner circle of Unit Disc Equation In general, a dirichlet problem in a region \(a\) asks you to solve a. One attractive feature of the circle $|z|=1$ is that. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial. Unit Disc Equation.
From www.mathworks.com
Poisson's Equation on Unit Disk PDE Modeler App MATLAB & Simulink Unit Disc Equation A closed unit disc is the set of points whose distance from p p is less than or equal to one: One attractive feature of the circle $|z|=1$ is that. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. Unit discs are a special case of unit ball. When you. Unit Disc Equation.
From www.researchgate.net
Solutions of Complex Differential Equation Having Pregiven Zeros in Unit Disc Equation First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. One attractive feature of the circle $|z|=1$ is that. Harmonic functions on the unit disk. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. When you mention the laplace. Unit Disc Equation.
From brainly.com
A unit disk centered at the origin is sliced so that the right portion Unit Disc Equation One attractive feature of the circle $|z|=1$ is that. When you mention the laplace equation, you probably have the disk in mind. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with. Unit Disc Equation.
From mikaem.github.io
Demo Helmholtz equation in polar coordinates — Shenfun executable demos Unit Disc Equation The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. One attractive feature of the circle $|z|=1$ is that. Harmonic functions on the unit disk. Unit discs are a special case of unit ball. A closed unit disc is the set of points whose distance from p p is. Unit Disc Equation.
From www.researchgate.net
(PDF) Families of Differential Equations in the Unit Disk Unit Disc Equation A closed unit disc is the set of points whose distance from p p is less than or equal to one: We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. Harmonic functions on the unit disk. The poisson formula enables us to solve the. Unit Disc Equation.
From www.chegg.com
Solved The unit disk D is one of the most important subsets Unit Disc Equation One attractive feature of the circle $|z|=1$ is that. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. In general, a dirichlet problem in a region \(a\) asks you to solve a. Harmonic functions on the unit disk. When you mention the laplace equation, you probably have the. Unit Disc Equation.
From www.youtube.com
Solution of the Poisson Equation on Unit Disk YouTube Unit Disc Equation Harmonic functions on the unit disk. One attractive feature of the circle $|z|=1$ is that. When you mention the laplace equation, you probably have the disk in mind. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. We started by assuming we had a harmonic function on the. Unit Disc Equation.
From www.numerade.com
SOLVEDShow that the image of the unit disc under the mapping (z + 1)2 Unit Disc Equation In general, a dirichlet problem in a region \(a\) asks you to solve a. One attractive feature of the circle $|z|=1$ is that. Harmonic functions on the unit disk. When you mention the laplace equation, you probably have the disk in mind. We started by assuming we had a harmonic function on the closed unit disk and we derived a. Unit Disc Equation.
From study.com
Disk Method Definition, Formula & Examples Video & Lesson Unit Disc Equation Unit discs are a special case of unit ball. We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. A closed unit disc is the set of points whose distance from p p is less than or equal to one: First parametrize the given surface. Unit Disc Equation.
From www.researchgate.net
(PDF) Fast growing solutions of linear differential equations with Unit Disc Equation In general, a dirichlet problem in a region \(a\) asks you to solve a. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel.. Unit Disc Equation.
From www.chegg.com
Consider the 2D heat equation on the unit disk with a Unit Disc Equation Unit discs are a special case of unit ball. A closed unit disc is the set of points whose distance from p p is less than or equal to one: Harmonic functions on the unit disk. In general, a dirichlet problem in a region \(a\) asks you to solve a. One attractive feature of the circle $|z|=1$ is that. First. Unit Disc Equation.
From www.researchgate.net
Graphical expressions of the unit disc in the complex plane Download Unit Disc Equation One attractive feature of the circle $|z|=1$ is that. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. In general, a dirichlet problem in a region \(a\) asks you to solve a. Unit discs are a special case of unit ball. We started by assuming we had a harmonic function. Unit Disc Equation.
From www.researchgate.net
(PDF) Growth and fixed points of solutions and their arbitraryorder Unit Disc Equation A closed unit disc is the set of points whose distance from p p is less than or equal to one: First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. When you mention the laplace equation, you probably have the disk in mind. Harmonic functions on the unit disk. In. Unit Disc Equation.
From www.adda247.com
Moment of Inertia Definition, Formula, Examples, Unit, Equations Unit Disc Equation We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. A closed unit disc is the set of points whose distance from p p is less than or equal to one: Harmonic functions on the unit disk. One attractive feature of the circle $|z|=1$ is. Unit Disc Equation.
From www.chegg.com
Solved 1. The unit disk D is one of the most important Unit Disc Equation The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. In general, a dirichlet problem in a region \(a\) asks you to solve a. One attractive feature of the circle $|z|=1$ is that. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial. Unit Disc Equation.
From www.youtube.com
6 2 The Disc Method YouTube Unit Disc Equation We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. In general, a dirichlet problem in a region \(a\) asks you to solve a. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. When you. Unit Disc Equation.
From www.researchgate.net
(PDF) On the [p; q]order of analytic solutions of linear differential Unit Disc Equation When you mention the laplace equation, you probably have the disk in mind. In general, a dirichlet problem in a region \(a\) asks you to solve a. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. Unit discs are a special case of unit ball. One attractive feature of the. Unit Disc Equation.
From www.researchgate.net
Derivation of a 1 and a 2 in a unit disk. Download Scientific Diagram Unit Disc Equation Harmonic functions on the unit disk. Unit discs are a special case of unit ball. A closed unit disc is the set of points whose distance from p p is less than or equal to one: First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. In general, a dirichlet problem. Unit Disc Equation.
From www.youtube.com
Derivation of Poisson's Formula for of Laplace's Equation on the Unit Unit Disc Equation A closed unit disc is the set of points whose distance from p p is less than or equal to one: One attractive feature of the circle $|z|=1$ is that. Unit discs are a special case of unit ball. Harmonic functions on the unit disk. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate. Unit Disc Equation.
From www.youtube.com
Tutorial Q43 Unit disc and unit circle relation to complex Unit Disc Equation We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. When you mention the laplace equation, you probably have the disk in mind. A closed unit disc is the set of points whose distance from p p is less than or equal to one: Harmonic. Unit Disc Equation.
From www.researchgate.net
Poisson equation on a unit disk. Plot of the analytical solution Unit Disc Equation The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. Harmonic functions on the unit disk. One attractive feature of the circle $|z|=1$ is that. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times. Unit discs are a special. Unit Disc Equation.
From www.researchgate.net
(PDF) The growth of solutions of linear differential equations with Unit Disc Equation A closed unit disc is the set of points whose distance from p p is less than or equal to one: Harmonic functions on the unit disk. In general, a dirichlet problem in a region \(a\) asks you to solve a. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then calculate $\frac{\partial g}{\partial u} \times.. Unit Disc Equation.
From www.researchgate.net
Unit disc with mesh. Download Scientific Diagram Unit Disc Equation In general, a dirichlet problem in a region \(a\) asks you to solve a. When you mention the laplace equation, you probably have the disk in mind. Unit discs are a special case of unit ball. We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson. Unit Disc Equation.
From www.youtube.com
Laplace Equation on the Unit Disk YouTube Unit Disc Equation We started by assuming we had a harmonic function on the closed unit disk and we derived a formula for it using the poisson kernel. The poisson formula enables us to solve the boundary value problem 2 = 0 in the unit disk, with prescribed values. First parametrize the given surface using $(x,y,z)= g(u,v)$ with $(u,v)$ in $w$ and then. Unit Disc Equation.