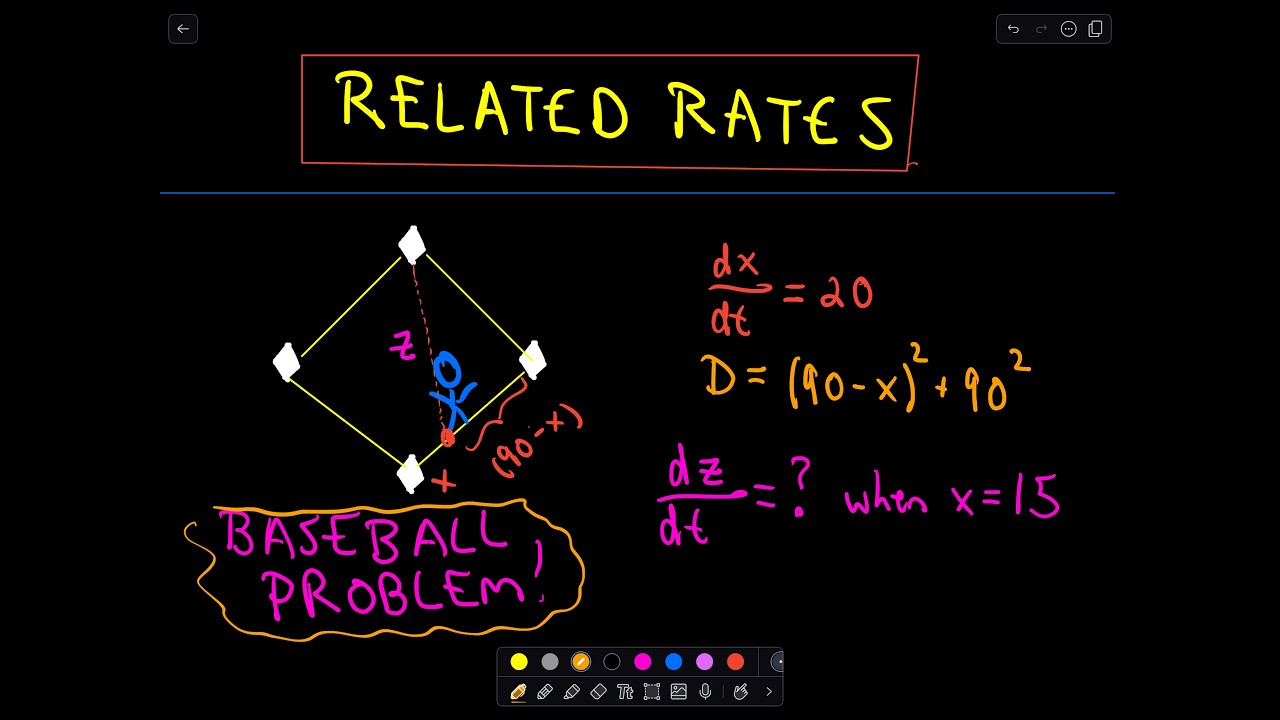
Baseball Diamond Related Rates . A batter hits the ball and runs toward first base with a speed of $f(t)$ ft/s after $t$. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. Find relationships among the derivatives in a given problem. Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. Use the chain rule to find the. A batter runs towards the first base with a speed of 20 ft/sec. How to relate different distances between a. 🏟️ the problem revolves around calculating the rate of change of distance between a baseball player and home plate while moving. In this video you will learn: A baseball diamond is a square with sides length 90 ft. Express changing quantities in terms of derivatives. A player runs from first base to second base at 15 ft/sec. A baseball diamond is a square with side length $90$ ft. A baseball diamond is a square 90 ft on a side.
from www.youtube.com
At what rate is the player's distance. Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. A baseball diamond is a square with sides length 90 ft. How to relate different distances between a. A batter runs towards the first base with a speed of 20 ft/sec. A baseball diamond is a square 90 ft on a side. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. Find relationships among the derivatives in a given problem. Use the chain rule to find the. Baseball example a baseball diamond is a square with side 90 ft.
Related Rates for Calculus Baseball Diamond Problem YouTube
Baseball Diamond Related Rates 🏟️ the problem revolves around calculating the rate of change of distance between a baseball player and home plate while moving. How to relate different distances between a. 🏟️ the problem revolves around calculating the rate of change of distance between a baseball player and home plate while moving. Find relationships among the derivatives in a given problem. Baseball example a baseball diamond is a square with side 90 ft. A baseball diamond is a square 90 ft on a side. A baseball diamond is a square with side length $90$ ft. Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. A batter runs towards the first base with a speed of 20 ft/sec. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. Express changing quantities in terms of derivatives. In this video you will learn: At what rate is the player's distance. Use the chain rule to find the. A baseball diamond is a square with sides length 90 ft. A player runs from first base to second base at 15 ft/sec.
From ar.inspiredpencil.com
Baseball Diamond Layout Positions Baseball Diamond Related Rates 🏟️ the problem revolves around calculating the rate of change of distance between a baseball player and home plate while moving. At what rate is the player's distance. A player runs from first base to second base at 15 ft/sec. A batter runs towards the first base with a speed of 20 ft/sec. A baseball diamond is a square 90. Baseball Diamond Related Rates.
From www.chegg.com
Solved 33. Baseball A baseball diamond has the shape of a Baseball Diamond Related Rates In this video you will learn: A baseball diamond is a square with sides length 90 ft. At what rate is the player's distance. A batter runs towards the first base with a speed of 20 ft/sec. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. Express changing quantities in terms of derivatives. A. Baseball Diamond Related Rates.
From stewart-switch.com
Printable Baseball Diamond Diagram Baseball Diamond Related Rates At what rate is the player's distance. A baseball diamond is a square 90 ft on a side. 🏟️ the problem revolves around calculating the rate of change of distance between a baseball player and home plate while moving. Use the chain rule to find the. A baseball diamond is a square with side length $90$ ft. A player runs. Baseball Diamond Related Rates.
From www.bartleby.com
Answered Consider the baseball diamond, which… bartleby Baseball Diamond Related Rates A baseball diamond is a square 90 ft on a side. At what rate is the player's distance. A batter runs towards the first base with a speed of 20 ft/sec. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. Use the chain rule to find the. A baseball diamond is a square with. Baseball Diamond Related Rates.
From www.pinterest.jp
How to Read the Pitching Lines in a Baseball Box Score Baseball score Baseball Diamond Related Rates Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. Baseball example a baseball diamond is a square with side 90 ft. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. Express changing quantities in terms of derivatives. A batter runs towards the first. Baseball Diamond Related Rates.
From www.vaperque.com
Baseball Field Dimensions Guide for All Leagues Anytime Baseball Supply Baseball Diamond Related Rates Baseball example a baseball diamond is a square with side 90 ft. A player runs from first base to second base at 15 ft/sec. A batter runs towards the first base with a speed of 20 ft/sec. 🏟️ the problem revolves around calculating the rate of change of distance between a baseball player and home plate while moving. Express changing. Baseball Diamond Related Rates.
From www.gauthmath.com
Solved A baseball diamond is a square with side 90 feet. A batter hits Baseball Diamond Related Rates Find relationships among the derivatives in a given problem. Baseball example a baseball diamond is a square with side 90 ft. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. At what rate is the player's distance. How to relate different distances between a. A player runs from first base to second base. Baseball Diamond Related Rates.
From www.youtube.com
Calculus 1 Related Rates Baseball Diamond YouTube Baseball Diamond Related Rates In this video you will learn: A baseball diamond is a square 90 ft on a side. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. A batter runs towards the first base with a speed of 20 ft/sec. A baseball diamond is a square with side length $90$ ft. How to relate. Baseball Diamond Related Rates.
From stewart-switch.com
Printable Baseball Diamond Diagram Baseball Diamond Related Rates A batter runs towards the first base with a speed of 20 ft/sec. A batter hits the ball and runs toward first base with a speed of $f(t)$ ft/s after $t$. A baseball diamond is a square 90 ft on a side. Express changing quantities in terms of derivatives. Find relationships among the derivatives in a given problem. A player. Baseball Diamond Related Rates.
From www.youtube.com
Related Rates Baseball Diamond Problem YouTube Baseball Diamond Related Rates Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. In this video you will learn: A baseball diamond is a square 90 ft on a side. Express changing quantities in terms of derivatives. A baseball diamond is a square with side length $90$ ft. A baseball diamond is a square. Baseball Diamond Related Rates.
From www.chegg.com
Solved A baseball diamond is a square with side 90 ft. A Baseball Diamond Related Rates Find relationships among the derivatives in a given problem. In this video you will learn: Use the chain rule to find the. How to relate different distances between a. A player runs from first base to second base at 15 ft/sec. At what rate is the player's distance. A batter hits the ball and runs toward first base with a. Baseball Diamond Related Rates.
From www.youtube.com
Related Rates Baseball Diamond A317 YouTube Baseball Diamond Related Rates At what rate is the player's distance. Baseball example a baseball diamond is a square with side 90 ft. Express changing quantities in terms of derivatives. A baseball diamond is a square 90 ft on a side. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. A baseball diamond is a square with side. Baseball Diamond Related Rates.
From www.chegg.com
Solved For the baseball diamond in Exercise 27, suppose the Baseball Diamond Related Rates A batter runs towards the first base with a speed of 20 ft/sec. How to relate different distances between a. A batter hits the ball and runs toward first base with a speed of $f(t)$ ft/s after $t$. Find relationships among the derivatives in a given problem. At what rate is the player's distance. A player runs from first base. Baseball Diamond Related Rates.
From mybackyardsports.com
How to Properly Measure a Baseball Diamond MyBackyard Sports Baseball Diamond Related Rates A baseball diamond is a square 90 ft on a side. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. Find relationships among the derivatives in a given problem. Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. 🏟️ the problem revolves around. Baseball Diamond Related Rates.
From cliparts.co
Baseball Diamond Diagram Cliparts.co Baseball Diamond Related Rates A batter hits the ball and runs toward first base with a speed of $f(t)$ ft/s after $t$. A baseball diamond is a square 90 ft on a side. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. Find relationships among the derivatives in a given problem. Use the chain rule to find the.. Baseball Diamond Related Rates.
From www.thoughtco.com
Sports Basics Softball and Baseball Rules and Regulations Baseball Diamond Related Rates At what rate is the player's distance. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. A baseball diamond is a square 90 ft on a side. A player runs from first base to. Baseball Diamond Related Rates.
From www.chegg.com
Solved 5) A baseball diamond has the shape of a square with Baseball Diamond Related Rates Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. Find relationships among the derivatives in a given problem. Use the chain rule to find the. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. In this video you will learn: A baseball diamond. Baseball Diamond Related Rates.
From kunduz.com
[ANSWERED] This diagram represents a baseball diamond. The infield Baseball Diamond Related Rates Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. At what rate is the player's distance. How to relate different distances between a. This calculus video tutorial explains how to solve the baseball diamond. Baseball Diamond Related Rates.
From www.youtube.com
MathCamp321 Calculus Related Rates (Baseball Diamond) YouTube Baseball Diamond Related Rates Baseball example a baseball diamond is a square with side 90 ft. A baseball diamond is a square with side length $90$ ft. At what rate is the player's distance. A batter runs towards the first base with a speed of 20 ft/sec. A player runs from first base to second base at 15 ft/sec. A baseball diamond is a. Baseball Diamond Related Rates.
From ar.inspiredpencil.com
Baseball Diamond Diagram With Positions Baseball Diamond Related Rates A player runs from first base to second base at 15 ft/sec. 🏟️ the problem revolves around calculating the rate of change of distance between a baseball player and home plate while moving. A batter runs towards the first base with a speed of 20 ft/sec. Find relationships among the derivatives in a given problem. At what rate is the. Baseball Diamond Related Rates.
From www.youtube.com
Activity 3.5.5 Related Rates Baseball Diamond YouTube Baseball Diamond Related Rates Use the chain rule to find the. How to relate different distances between a. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. A baseball diamond is a square with sides length 90 ft. Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond.. Baseball Diamond Related Rates.
From www.youtube.com
Related Rates The Baseball Diamond Problem YouTube Baseball Diamond Related Rates How to relate different distances between a. 🏟️ the problem revolves around calculating the rate of change of distance between a baseball player and home plate while moving. In this video you will learn: A baseball diamond is a square 90 ft on a side. A batter hits the ball and runs toward rst base with a speed of 24. Baseball Diamond Related Rates.
From www.youtube.com
Calculus Related Rates Baseball Diamond YouTube Baseball Diamond Related Rates How to relate different distances between a. A player runs from first base to second base at 15 ft/sec. A batter hits the ball and runs toward first base with a speed of $f(t)$ ft/s after $t$. A baseball diamond is a square with side length $90$ ft. Baseball example a baseball diamond is a square with side 90 ft.. Baseball Diamond Related Rates.
From www.youtube.com
Calculus Related Rates The Baseball Diamond Problem YouTube Baseball Diamond Related Rates How to relate different distances between a. Use the chain rule to find the. A baseball diamond is a square with sides length 90 ft. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. A player runs from first base to second base at 15 ft/sec. Video on a calculus 1 topic where. Baseball Diamond Related Rates.
From www.chegg.com
Solved A baseball diamond has the shape of a square with Baseball Diamond Related Rates Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. A baseball diamond is a square with side length $90$ ft. Express changing quantities in terms of derivatives. A batter hits the ball and runs. Baseball Diamond Related Rates.
From www.sfchronicle.com
Imperfect diamond Myths of MLB geometry revealed by new larger bases Baseball Diamond Related Rates How to relate different distances between a. Baseball example a baseball diamond is a square with side 90 ft. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. Use the chain rule to find the. A baseball diamond is a square 90 ft on a side. At what rate is the player's distance. Express. Baseball Diamond Related Rates.
From www.youtube.com
Related Rates for Calculus Baseball Diamond Problem YouTube Baseball Diamond Related Rates This calculus video tutorial explains how to solve the baseball diamond problem in related rates. A player runs from first base to second base at 15 ft/sec. Express changing quantities in terms of derivatives. At what rate is the player's distance. A baseball diamond is a square with side length $90$ ft. A batter hits the ball and runs toward. Baseball Diamond Related Rates.
From quizlet.com
A baseball diamond is a square with side 90 ft. A batter hit Quizlet Baseball Diamond Related Rates At what rate is the player's distance. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. A baseball diamond is a square with sides length 90 ft. Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. A baseball diamond is a square 90 ft. Baseball Diamond Related Rates.
From ar.inspiredpencil.com
Baseball Rates Baseball Diamond Related Rates Express changing quantities in terms of derivatives. A baseball diamond is a square 90 ft on a side. Baseball example a baseball diamond is a square with side 90 ft. A baseball diamond is a square with side length $90$ ft. How to relate different distances between a. Video on a calculus 1 topic where we work through solving a. Baseball Diamond Related Rates.
From www.youtube.com
Related Rates Baseball Diamond Problem JK Math YouTube Baseball Diamond Related Rates Find relationships among the derivatives in a given problem. A batter hits the ball and runs toward rst base with a speed of 24 ft/s. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. A batter hits the ball and runs toward first base with a speed of $f(t)$ ft/s after $t$. Use the. Baseball Diamond Related Rates.
From www.chegg.com
Solved A baseball diamond is a square with side 90 ft. A Baseball Diamond Related Rates A batter hits the ball and runs toward first base with a speed of $f(t)$ ft/s after $t$. Express changing quantities in terms of derivatives. In this video you will learn: Baseball example a baseball diamond is a square with side 90 ft. At what rate is the player's distance. Use the chain rule to find the. How to relate. Baseball Diamond Related Rates.
From www.youtube.com
Baseball Diamond Related Rate YouTube Baseball Diamond Related Rates Use the chain rule to find the. Video on a calculus 1 topic where we work through solving a related rates problem involving a baseball diamond. How to relate different distances between a. In this video you will learn: At what rate is the player's distance. A batter hits the ball and runs toward first base with a speed of. Baseball Diamond Related Rates.
From www.chegg.com
Solved 24. A baseball diamond is a square 90 ft on a side. A Baseball Diamond Related Rates A baseball diamond is a square with sides length 90 ft. A player runs from first base to second base at 15 ft/sec. A baseball diamond is a square 90 ft on a side. This calculus video tutorial explains how to solve the baseball diamond problem in related rates. Use the chain rule to find the. Express changing quantities in. Baseball Diamond Related Rates.
From www.chegg.com
Solved A baseball diamond is a square with side 90 ft. A Baseball Diamond Related Rates Baseball example a baseball diamond is a square with side 90 ft. Use the chain rule to find the. Express changing quantities in terms of derivatives. Find relationships among the derivatives in a given problem. A baseball diamond is a square with side length $90$ ft. A batter hits the ball and runs toward rst base with a speed of. Baseball Diamond Related Rates.
From www.studocu.com
0309020 Related Rates Calculus I, Section 3, Related Rates A Baseball Diamond Related Rates Use the chain rule to find the. In this video you will learn: A baseball diamond is a square with side length $90$ ft. A baseball diamond is a square with sides length 90 ft. A batter runs towards the first base with a speed of 20 ft/sec. Express changing quantities in terms of derivatives. Video on a calculus 1. Baseball Diamond Related Rates.