Prove That The Derivative Of Cot X Csc 2X . Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. Differentiate using the quotient rule. We start by defining cot (x) as cos (x) sin (x). Given f (x) = g(x) h(x) then. F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: It refers to the process of finding the change in the sine function with respect to the independent variable. This derivative can be proved using limits and trigonometric identities. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. Learn the derivative of cot x along with its proof and also see some examples using the same.
from www.youtube.com
This derivative can be proved using limits and trigonometric identities. We start by defining cot (x) as cos (x) sin (x). Learn the derivative of cot x along with its proof and also see some examples using the same. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. Differentiate using the quotient rule. Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. It refers to the process of finding the change in the sine function with respect to the independent variable. Given f (x) = g(x) h(x) then.
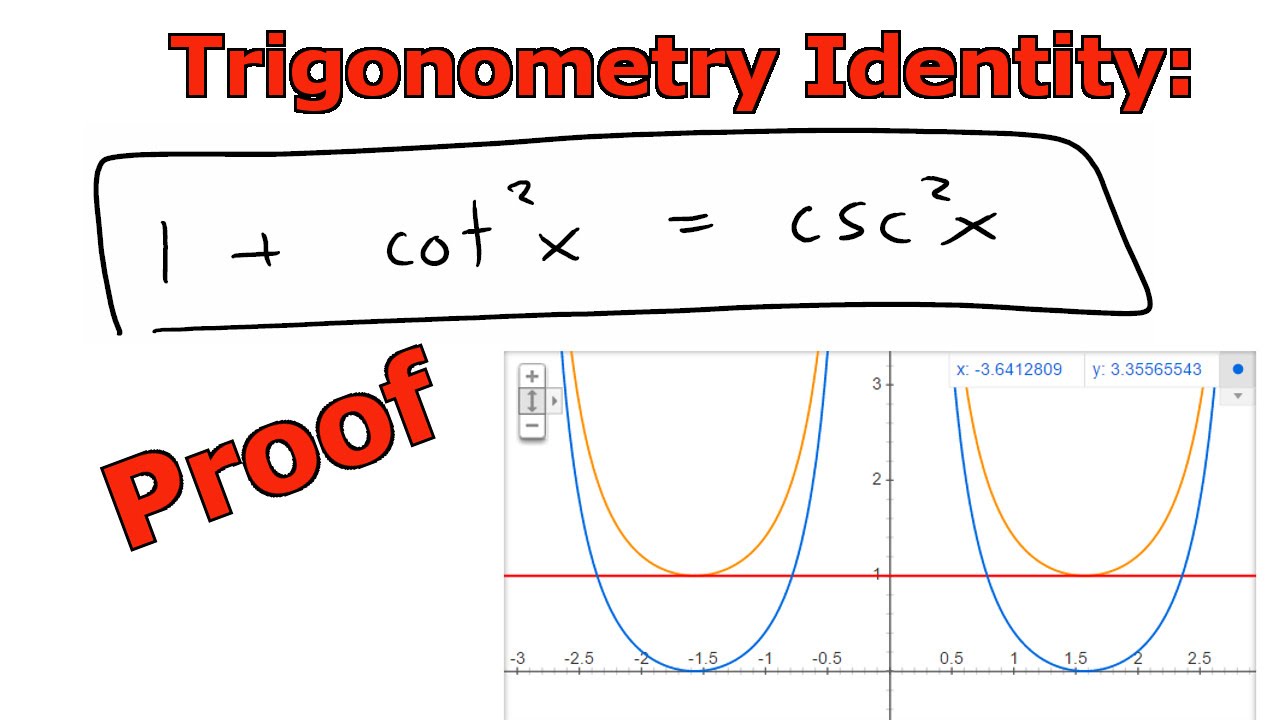
Trigonometry Identity 1 + cot^2(x) = csc^2(x) YouTube
Prove That The Derivative Of Cot X Csc 2X This derivative can be proved using limits and trigonometric identities. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. It refers to the process of finding the change in the sine function with respect to the independent variable. F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). This derivative can be proved using limits and trigonometric identities. Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. We start by defining cot (x) as cos (x) sin (x). Differentiate using the quotient rule. Learn the derivative of cot x along with its proof and also see some examples using the same. Given f (x) = g(x) h(x) then.
From www.youtube.com
Derivative of csc(x) Proof YouTube Prove That The Derivative Of Cot X Csc 2X This derivative can be proved using limits and trigonometric identities. We start by defining cot (x) as cos (x) sin (x). Learn the derivative of cot x along with its proof and also see some examples using the same. Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change. Prove That The Derivative Of Cot X Csc 2X.
From www.bytelearn.com
Cot Derivative Definition, Examples & Practice Problems Prove That The Derivative Of Cot X Csc 2X Given f (x) = g(x) h(x) then. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. This derivative can be proved using limits and trigonometric identities. Differentiate using the quotient rule. Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. It refers to the process of finding the change. Prove That The Derivative Of Cot X Csc 2X.
From peakd.com
Derivative of csc(x) Proof PeakD Prove That The Derivative Of Cot X Csc 2X Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. It refers to the process of finding the change in the sine function with respect to the independent variable. Learn the derivative of cot x along with its proof and also see some examples. Prove That The Derivative Of Cot X Csc 2X.
From www.youtube.com
Derivative of Cot x (Proof) d/dx (cot x) = cosec^2 x Prove That The Derivative Of Cot X Csc 2X Learn the derivative of cot x along with its proof and also see some examples using the same. Differentiate using the quotient rule. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. It refers to the process of finding the. Prove That The Derivative Of Cot X Csc 2X.
From www.numerade.com
SOLVEDProve that (d)/(dx) (cot x ) = csc^2 x. Prove That The Derivative Of Cot X Csc 2X Learn the derivative of cot x along with its proof and also see some examples using the same. This derivative can be proved using limits and trigonometric identities. We start by defining cot (x) as cos (x) sin (x). Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change. Prove That The Derivative Of Cot X Csc 2X.
From www.youtube.com
Calculus Differentiation Derivative of Csc x from first principle Prove That The Derivative Of Cot X Csc 2X F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). Learn the derivative of cot x along with its proof and also see some examples using the same. This derivative can be proved using limits and trigonometric identities. We start by defining cot (x) as cos (x) sin (x). Derivative of cot x is also known as differentiation of cot x which is the process. Prove That The Derivative Of Cot X Csc 2X.
From www.youtube.com
Prove the trigonometry identity 1+cot^2x=csc^2x YouTube Prove That The Derivative Of Cot X Csc 2X X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). Differentiate using the quotient rule. This derivative can be proved using limits and trigonometric identities. It refers to the process of finding the change in the sine function with respect to the independent variable. Given f (x) = g(x) h(x) then. Learn the derivative of cot. Prove That The Derivative Of Cot X Csc 2X.
From www.numerade.com
SOLVEDUse the quotient rule and the derivatives of the sine and cosine Prove That The Derivative Of Cot X Csc 2X Learn the derivative of cot x along with its proof and also see some examples using the same. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: It refers to the process of finding the change in the sine function with respect to the independent variable. This derivative can be proved using limits and trigonometric identities. We start by defining. Prove That The Derivative Of Cot X Csc 2X.
From www.epsilonify.com
What is the integral of csc^2(x)? Epsilonify Prove That The Derivative Of Cot X Csc 2X X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. Learn the derivative of cot x along with its proof and also see some examples using the same. Given f (x) = g(x) h(x) then. Derivative of cot x is also known. Prove That The Derivative Of Cot X Csc 2X.
From www.numerade.com
SOLVED Prove that (d)/(dx)(csc x)=csc x cot x Prove That The Derivative Of Cot X Csc 2X It refers to the process of finding the change in the sine function with respect to the independent variable. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Learn the derivative of cot x along with its proof and also see some examples using the same. We start by defining cot (x) as cos (x) sin (x). F '(x) =. Prove That The Derivative Of Cot X Csc 2X.
From www.epsilonify.com
What is the Derivative of csc^2(x)? Epsilonify Prove That The Derivative Of Cot X Csc 2X We start by defining cot (x) as cos (x) sin (x). F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Given f (x) = g(x) h(x) then. This derivative can be proved using limits and trigonometric identities. Derivative of cot x is also known as differentiation of cot x which. Prove That The Derivative Of Cot X Csc 2X.
From en.neurochispas.com
Derivative of Cosecant Squared, csc^2(x) with Proof and Graphs Prove That The Derivative Of Cot X Csc 2X It refers to the process of finding the change in the sine function with respect to the independent variable. Given f (x) = g(x) h(x) then. We start by defining cot (x) as cos (x) sin (x). Differentiate using the quotient rule. Learn the derivative of cot x along with its proof and also see some examples using the same.. Prove That The Derivative Of Cot X Csc 2X.
From www.epsilonify.com
What is the Derivative of Square Root of x^2 + 1? Epsilonify Prove That The Derivative Of Cot X Csc 2X Differentiate using the quotient rule. We start by defining cot (x) as cos (x) sin (x). This derivative can be proved using limits and trigonometric identities. Learn the derivative of cot x along with its proof and also see some examples using the same. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. It refers to the process of. Prove That The Derivative Of Cot X Csc 2X.
From www.numerade.com
SOLVED Show that the derivative of cot x is csc^2x. (Derive d/dx[cot Prove That The Derivative Of Cot X Csc 2X Differentiate using the quotient rule. This derivative can be proved using limits and trigonometric identities. Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. Learn the derivative of cot x along with its proof and also see some examples using the same. F. Prove That The Derivative Of Cot X Csc 2X.
From www.chegg.com
Solved Question 6 Find the derivative. y = (csc x + cot Prove That The Derivative Of Cot X Csc 2X Differentiate using the quotient rule. F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). This derivative can be proved using limits and trigonometric identities. We start by defining cot (x) as cos (x) sin (x). Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: F. Prove That The Derivative Of Cot X Csc 2X.
From www.meritnation.com
Derivative of cot2x How is it 2cosec^2 2x Maths 9910734 Prove That The Derivative Of Cot X Csc 2X Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Differentiate using the quotient rule. This derivative can be proved using limits and trigonometric identities. Learn how to prove the trigonometric identity 1 + cot². Prove That The Derivative Of Cot X Csc 2X.
From www.youtube.com
Derivative of cot(x) Proof YouTube Prove That The Derivative Of Cot X Csc 2X We start by defining cot (x) as cos (x) sin (x). Differentiate using the quotient rule. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). Given f (x) = g(x) h(x) then. This derivative can be proved using limits and trigonometric identities. Learn how to prove the trigonometric identity 1 + cot² x =. Prove That The Derivative Of Cot X Csc 2X.
From www.youtube.com
Integration by u Substitution Integral of cot^2(x)csc^2(x) dx YouTube Prove That The Derivative Of Cot X Csc 2X It refers to the process of finding the change in the sine function with respect to the independent variable. Learn the derivative of cot x along with its proof and also see some examples using the same. F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). We start by defining cot (x) as cos (x) sin (x). Differentiate using the quotient rule. F '(x). Prove That The Derivative Of Cot X Csc 2X.
From socratic.org
How do you verify cot^2x * sec^2x = csc^2x? Socratic Prove That The Derivative Of Cot X Csc 2X F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: This derivative can be proved using limits and trigonometric identities. Differentiate using the quotient rule. Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. Learn the. Prove That The Derivative Of Cot X Csc 2X.
From www.numerade.com
SOLVED Derive the given formulas from the derivatives of sine and Prove That The Derivative Of Cot X Csc 2X It refers to the process of finding the change in the sine function with respect to the independent variable. Given f (x) = g(x) h(x) then. This derivative can be proved using limits and trigonometric identities. We start by defining cot (x) as cos (x) sin (x). F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. Learn the derivative. Prove That The Derivative Of Cot X Csc 2X.
From www.showme.com
Derivative of csc^2(x) Math, Trigonometric Functions, Derivatives Prove That The Derivative Of Cot X Csc 2X It refers to the process of finding the change in the sine function with respect to the independent variable. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. We start by defining cot (x) as cos (x) sin (x). This derivative can be proved using limits and trigonometric identities. F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). Derivative of cot x is. Prove That The Derivative Of Cot X Csc 2X.
From gbu-presnenskij.ru
SOLVED Verify The Identity Sin X Sin X Cot 2X Csc X, 49 OFF Prove That The Derivative Of Cot X Csc 2X This derivative can be proved using limits and trigonometric identities. Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Given f (x) = g(x) h(x) then. Derivative of cot x is also known as differentiation of cot x which is the. Prove That The Derivative Of Cot X Csc 2X.
From www.gauthmath.com
Solved 19. Prove that d/dx (cot x)=csc^2x. [Calculus] Prove That The Derivative Of Cot X Csc 2X We start by defining cot (x) as cos (x) sin (x). F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. It refers to the process of finding the change in the sine function with respect to the independent variable. Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. Learn. Prove That The Derivative Of Cot X Csc 2X.
From www.transtutors.com
(Get Answer) Find The Derivative. Y = (Csc X + Cot X) (Csc X Cot X Prove That The Derivative Of Cot X Csc 2X Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. Given f (x) = g(x) h(x) then. Learn the derivative of cot x along with. Prove That The Derivative Of Cot X Csc 2X.
From www.numerade.com
SOLVEDUse the quotient rule and the derivatives of the sine and cosine Prove That The Derivative Of Cot X Csc 2X Differentiate using the quotient rule. Given f (x) = g(x) h(x) then. Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: It refers to the process of finding the change in the sine function with respect to the independent variable. Learn. Prove That The Derivative Of Cot X Csc 2X.
From www.gauthmath.com
Solved Compute for the derivative of the given function for x=2. The Prove That The Derivative Of Cot X Csc 2X F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Differentiate using the quotient rule. F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). Learn the derivative of cot x along with its proof and also see some examples using the same. This derivative can be proved using limits and trigonometric identities. It refers to. Prove That The Derivative Of Cot X Csc 2X.
From www.chegg.com
Solved (3) Show that the derivative of csc(x)=−csc(x)cot(x). Prove That The Derivative Of Cot X Csc 2X F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. Differentiate using the quotient rule. It refers to the process of finding the change in the sine function with respect to the independent variable. We start by defining cot. Prove That The Derivative Of Cot X Csc 2X.
From buzzar-brandi.blogspot.com
Brandi's Buzzar Blog Proof Derivative cot x = csc^2 x Prove That The Derivative Of Cot X Csc 2X Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. Learn the derivative of cot x along with its proof and also see some examples. Prove That The Derivative Of Cot X Csc 2X.
From derivativeit.com
The Derivative of csc^2x DerivativeIt Prove That The Derivative Of Cot X Csc 2X It refers to the process of finding the change in the sine function with respect to the independent variable. Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. Given f (x) = g(x) h(x) then. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx).. Prove That The Derivative Of Cot X Csc 2X.
From www.gauthmath.com
Solved What is the derivative of cscx? sec (x)tan (x) sec (x)tan (x Prove That The Derivative Of Cot X Csc 2X This derivative can be proved using limits and trigonometric identities. It refers to the process of finding the change in the sine function with respect to the independent variable. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Differentiate using the quotient rule. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. Learn the derivative of cot x along. Prove That The Derivative Of Cot X Csc 2X.
From www.youtube.com
Trigonometry Identity 1 + cot^2(x) = csc^2(x) YouTube Prove That The Derivative Of Cot X Csc 2X We start by defining cot (x) as cos (x) sin (x). Learn how to prove the trigonometric identity 1 + cot² x = csc² x using algebraic manipulation and trigonometric. Given f (x) = g(x) h(x) then. Differentiate using the quotient rule. Derivative of cot x is also known as differentiation of cot x which is the process of finding. Prove That The Derivative Of Cot X Csc 2X.
From www.youtube.com
Evaluate the Integral sqrt(cot x) csc^2 x dx using the substitution Prove That The Derivative Of Cot X Csc 2X F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). Learn the derivative of cot x along with its proof and also see some examples using the same. Differentiate using the quotient rule. We start by defining cot (x) as cos (x) sin (x). This derivative can be proved using limits and trigonometric identities. F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. Derivative. Prove That The Derivative Of Cot X Csc 2X.
From www.numerade.com
SOLVEDProve the given identities. \tan x+\cot x=\tan x \csc ^{2} x Prove That The Derivative Of Cot X Csc 2X Learn the derivative of cot x along with its proof and also see some examples using the same. Given f (x) = g(x) h(x) then. F' (x)=d/dx (cosx/sinx)= (sinx (d/dxcosx). X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: We start by defining cot (x) as cos (x) sin (x). Derivative of cot x is also known as differentiation of. Prove That The Derivative Of Cot X Csc 2X.
From www.chegg.com
Solved Find the derivative. y = (csc X+cot x)(csc X cotx) Prove That The Derivative Of Cot X Csc 2X F '(x) = h(x)g'(x) − g(x)h'(x) (h(x))2 ← quotient rule. Given f (x) = g(x) h(x) then. Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the cot trigonometric function. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: It refers to the process of finding the. Prove That The Derivative Of Cot X Csc 2X.
From www.epsilonify.com
Derivative of csc(x) using First Principle of Derivatives [Full Proof] Prove That The Derivative Of Cot X Csc 2X We start by defining cot (x) as cos (x) sin (x). Given f (x) = g(x) h(x) then. It refers to the process of finding the change in the sine function with respect to the independent variable. Derivative of cot x is also known as differentiation of cot x which is the process of finding rate of change in the. Prove That The Derivative Of Cot X Csc 2X.