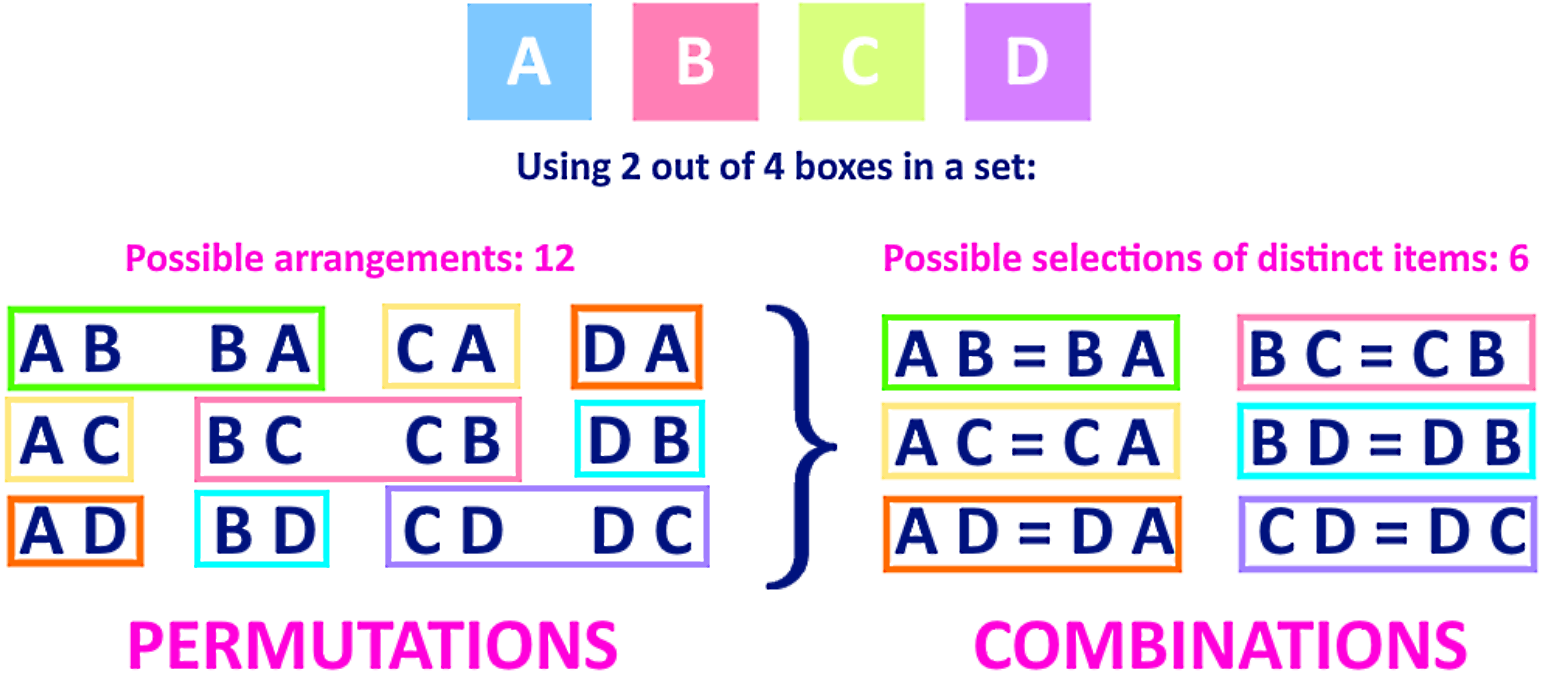
Combination And Permutation Repetition . Permutations arrange objects where order matters while combinations select objects where order does not matter. Example \ (\pageindex {2}\) example with restrictions. Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects of. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of.
from www.studypug.com
Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Example \ (\pageindex {2}\) example with restrictions. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects of. Permutations arrange objects where order matters while combinations select objects where order does not matter. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset.
Understanding permutations vs. combinations StudyPug
Combination And Permutation Repetition Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Permutations arrange objects where order matters while combinations select objects where order does not matter. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects of. Example \ (\pageindex {2}\) example with restrictions.
From www.slideserve.com
PPT Generalized Permutations and Combinations PowerPoint Presentation Combination And Permutation Repetition When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects of. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a. Combination And Permutation Repetition.
From simp-link.com
Permutation with repetition algorithm Combination And Permutation Repetition I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects of. Enumerative combinatorics explores counting techniques for. Combination And Permutation Repetition.
From www.slideserve.com
PPT Permutations with Repetition PowerPoint Presentation, free Combination And Permutation Repetition I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Permutations arrange objects where order matters while combinations select objects where order does not matter. Example \ (\pageindex {2}\) example with restrictions. Given a set of \ (n\) objects. Combination And Permutation Repetition.
From www.slideserve.com
PPT 5.5 Generalized Permutations and Combinations PowerPoint Combination And Permutation Repetition Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. Permutations arrange objects where order matters while combinations select objects where order does not matter. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. I another way to see this:compute. Combination And Permutation Repetition.
From www.slideserve.com
PPT Generalized Permutations and Combinations PowerPoint Presentation Combination And Permutation Repetition Permutations arrange objects where order matters while combinations select objects where order does not matter. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. Example \ (\pageindex {2}\) example with restrictions. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. When a permutation can repeat,. Combination And Permutation Repetition.
From www.youtube.com
Permutations and Combinations7/ permutation with repetition YouTube Combination And Permutation Repetition Example \ (\pageindex {2}\) example with restrictions. Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects of. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Permutation and combination are various ways of. Combination And Permutation Repetition.
From www.youtube.com
PERMUTATION AND COMBINATION Part 2c Permutation Involving Arrangements Combination And Permutation Repetition Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Example \ (\pageindex {2}\). Combination And Permutation Repetition.
From www.slideserve.com
PPT Permutations with Repetition PowerPoint Presentation, free Combination And Permutation Repetition Example \ (\pageindex {2}\) example with restrictions. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Permutations arrange objects where order matters while combinations select objects where order does not matter. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial. Combination And Permutation Repetition.
From www.cuemath.com
Permutation and Combination Definition, Formulas, Derivation, Examples Combination And Permutation Repetition Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Example \ (\pageindex {2}\) example with restrictions. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative. Combination And Permutation Repetition.
From www.youtube.com
Permutations with Repetition Combinatorics, Permutations and Combination And Permutation Repetition Permutations arrange objects where order matters while combinations select objects where order does not matter. Example \ (\pageindex {2}\) example with restrictions. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial. Combination And Permutation Repetition.
From www.slideserve.com
PPT Generalized Permutations and Combinations PowerPoint Presentation Combination And Permutation Repetition I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Example \ (\pageindex {2}\) example with restrictions. Permutations arrange objects where order matters while combinations select objects where order does not matter. Permutation and combination are various ways of. Combination And Permutation Repetition.
From www.youtube.com
Permutations and Combinations lesson 5 Permutations with repetition Combination And Permutation Repetition Example \ (\pageindex {2}\) example with restrictions. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. I another way to see this:compute total # of permutations ( n !). Combination And Permutation Repetition.
From www.slideserve.com
PPT ProbabilityIII (Permutations and Combinations) PowerPoint Combination And Permutation Repetition Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects of. Example \ (\pageindex {2}\) example with restrictions. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), #. Combination And Permutation Repetition.
From www.youtube.com
Arrangement with repetition in Permutation Permutation and Combination And Permutation Repetition Permutations arrange objects where order matters while combinations select objects where order does not matter. Example \ (\pageindex {2}\) example with restrictions. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Enumerative combinatorics explores counting techniques for finite. Combination And Permutation Repetition.
From www.studypug.com
Understanding permutations vs. combinations StudyPug Combination And Permutation Repetition Permutations arrange objects where order matters while combinations select objects where order does not matter. Example \ (\pageindex {2}\) example with restrictions. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. Given a set of \. Combination And Permutation Repetition.
From www.youtube.com
Lesson 67 Generalized Permutations and Combinations Combinations Combination And Permutation Repetition When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings. Combination And Permutation Repetition.
From www.slideserve.com
PPT Generalized Permutations and Combinations PowerPoint Presentation Combination And Permutation Repetition Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings. Combination And Permutation Repetition.
From www.youtube.com
MAT3720 3.6 Permutations and Combinations with Repetition YouTube Combination And Permutation Repetition When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Example \ (\pageindex {2}\) example with restrictions. Permutations arrange objects where order matters while combinations select objects where order does not matter. Permutation and combination are various ways of representing grouped data by rearranging them in a. Combination And Permutation Repetition.
From www.slideserve.com
PPT Generalized Permutations and Combinations PowerPoint Presentation Combination And Permutation Repetition When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Example \ (\pageindex {2}\) example with restrictions. Given a set of \ (n\) objects such that there are \ (n_1\). Combination And Permutation Repetition.
From www.slideshare.net
Permutation combination Combination And Permutation Repetition Example \ (\pageindex {2}\) example with restrictions. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\). Combination And Permutation Repetition.
From www.slideserve.com
PPT Generalized Permutations and Combinations PowerPoint Presentation Combination And Permutation Repetition I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Example \ (\pageindex {2}\) example with restrictions. Permutations arrange objects where order matters while combinations select objects where order does not matter. Permutation and combination are various ways of. Combination And Permutation Repetition.
From www.slideserve.com
PPT Permutations & Combinations PowerPoint Presentation, free Combination And Permutation Repetition Permutations arrange objects where order matters while combinations select objects where order does not matter. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between. Combination And Permutation Repetition.
From www.slideserve.com
PPT 5.5 Generalized Permutations and Combinations PowerPoint Combination And Permutation Repetition Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects of. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Permutation and combination are various ways. Combination And Permutation Repetition.
From simp-link.com
Permutation with repetition algorithm Combination And Permutation Repetition Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. Example \ (\pageindex {2}\) example with restrictions. Permutations arrange objects where order matters while combinations select objects where order does not matter. Given a set of \. Combination And Permutation Repetition.
From www.slideserve.com
PPT Generalized Permutations and Combinations PowerPoint Presentation Combination And Permutation Repetition When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Given a set of \ (n\). Combination And Permutation Repetition.
From simp-link.com
Permutation with repetition algorithm Combination And Permutation Repetition Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative. Combination And Permutation Repetition.
From www.slideserve.com
PPT Permutations and Combinations PowerPoint Presentation, free Combination And Permutation Repetition Permutations arrange objects where order matters while combinations select objects where order does not matter. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Permutation and combination are various ways. Combination And Permutation Repetition.
From www.slideserve.com
PPT Combinations & Permutations PowerPoint Presentation, free Combination And Permutation Repetition Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects of. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. Example \ (\pageindex {2}\). Combination And Permutation Repetition.
From www.slideserve.com
PPT Combinations & Permutations PowerPoint Presentation, free Combination And Permutation Repetition When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Example \ (\pageindex {2}\) example with restrictions. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. Given a set of \ (n\) objects such that there are \ (n_1\) identical. Combination And Permutation Repetition.
From calcworkshop.com
Combinations (Illustrated w/ 11+ Worked Examples!) Combination And Permutation Repetition Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. Permutations arrange objects where order matters while combinations select objects where order does not matter. Given a set of \. Combination And Permutation Repetition.
From www.qualitygurus.com
Permutations and Combination Quality Gurus Combination And Permutation Repetition Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. When a permutation can repeat, we just need to raise n to. Combination And Permutation Repetition.
From www.youtube.com
Permutations and Combinations repetition Introduction YouTube Combination And Permutation Repetition I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Example \ (\pageindex {2}\) example with restrictions. Enumerative combinatorics explores counting techniques for finite sets, with combinations with repetition forming a crucial subset. When a permutation can repeat, we. Combination And Permutation Repetition.
From www.studypug.com
Understanding permutations vs. combinations StudyPug Combination And Permutation Repetition When a permutation can repeat, we just need to raise n to the power of however many objects from n we are choosing,. I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Given a set of \ (n\). Combination And Permutation Repetition.
From www.slideserve.com
PPT THE BASIC OF COUNTING PowerPoint Presentation, free download ID Combination And Permutation Repetition I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Example \ (\pageindex {2}\) example with restrictions. Given a set of \ (n\) objects such that there are \ (n_1\) identical objects of type 1, \ (n_2\) identical objects. Combination And Permutation Repetition.
From www.slideserve.com
PPT Permutations and Combinations PowerPoint Presentation, free Combination And Permutation Repetition I another way to see this:compute total # of permutations ( n !) and then divide by # of relative orderings between objects of type 1 (n 1 !), # of. Permutation and combination are various ways of representing grouped data by rearranging them in a specific manner. Example \ (\pageindex {2}\) example with restrictions. Enumerative combinatorics explores counting techniques. Combination And Permutation Repetition.