Generator Math Definition . As an example, remember the dihedral group, the symmetries of an n. A set of generators is a set of group elements such that possibly repeated application of the generators. I know the definition of group generators: A 0, a 1,., a n,. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. Generators are some special elements that we pick out which can be used to get to any other element in the group. A group $g$ is generated by $h\subseteq g$ if you can take the elements. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. This is how generated by usually works in algebra. The corresponding generating function f(x) f (x) is the series. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly.
from www.chegg.com
I know the definition of group generators: This is how generated by usually works in algebra. Generators are some special elements that we pick out which can be used to get to any other element in the group. As an example, remember the dihedral group, the symmetries of an n. The corresponding generating function f(x) f (x) is the series. A set of generators is a set of group elements such that possibly repeated application of the generators. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. A 0, a 1,., a n,. A group $g$ is generated by $h\subseteq g$ if you can take the elements.
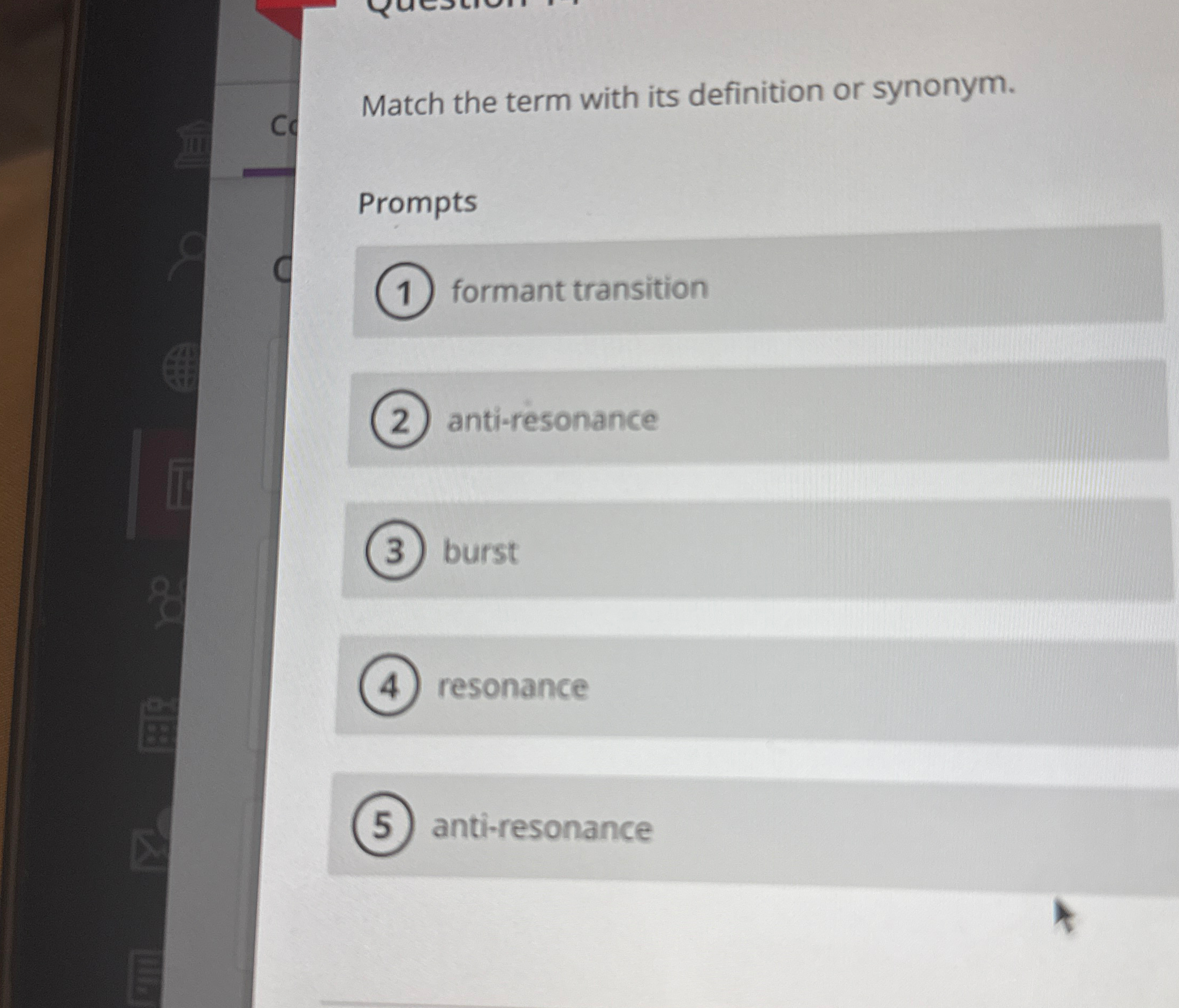
Solved cc Match the term with its definition or
Generator Math Definition A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. The corresponding generating function f(x) f (x) is the series. Generators are some special elements that we pick out which can be used to get to any other element in the group. A group $g$ is generated by $h\subseteq g$ if you can take the elements. As an example, remember the dihedral group, the symmetries of an n. I know the definition of group generators: A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. A set of generators is a set of group elements such that possibly repeated application of the generators. A 0, a 1,., a n,. This is how generated by usually works in algebra. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly.
From www.chegg.com
Solved Question 17 of 20Select the correct definition of Generator Math Definition The corresponding generating function f(x) f (x) is the series. As an example, remember the dihedral group, the symmetries of an n. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. I. Generator Math Definition.
From www.tessshebaylo.com
Random Math Equation Generator Tessshebaylo Generator Math Definition As an example, remember the dihedral group, the symmetries of an n. This is how generated by usually works in algebra. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. The corresponding generating function f(x) f (x) is the series. I know the definition of group. Generator Math Definition.
From pacgageblos.blogspot.com
Function Tables Worksheet / Patterns And Equations Worksheet Pattern Generator Math Definition The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. This is how generated by usually works in algebra. The corresponding generating function f(x) f (x) is the series. A 0, a 1,., a n,. Generators are some special elements that we pick out which can be. Generator Math Definition.
From studyx.ai
Definition if something happens I it happens StudyX Generator Math Definition This is how generated by usually works in algebra. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. The corresponding generating function f(x) f (x) is the series. A group $g$ is generated by $h\subseteq g$ if you can take the elements. The definitions of generating set of a group using finite sums, given above,. Generator Math Definition.
From www.slideshare.net
Discrete math Truth Table Generator Math Definition The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. As an example, remember the dihedral group, the symmetries of an n. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. I know. Generator Math Definition.
From materialzonevalentin.z21.web.core.windows.net
Math Worksheet Creator Generator Math Definition A set of generators is a set of group elements such that possibly repeated application of the generators. The corresponding generating function f(x) f (x) is the series. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a. Generator Math Definition.
From worksheetfullhoniara.z22.web.core.windows.net
Generate Free Math Worksheets Generator Math Definition Generators are some special elements that we pick out which can be used to get to any other element in the group. This is how generated by usually works in algebra. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. The corresponding generating function f(x) f. Generator Math Definition.
From dictionary.langeek.co
Definition & Meaning of "Generator" LanGeek Generator Math Definition As an example, remember the dihedral group, the symmetries of an n. A 0, a 1,., a n,. The corresponding generating function f(x) f (x) is the series. A set of generators is a set of group elements such that possibly repeated application of the generators. A group $g$ is generated by $h\subseteq g$ if you can take the elements.. Generator Math Definition.
From studylib.net
Function Generator Generator Math Definition This is how generated by usually works in algebra. As an example, remember the dihedral group, the symmetries of an n. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. A group. Generator Math Definition.
From lilianweng.github.io
What are Diffusion Models? Generator Math Definition A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. The corresponding generating function f(x) f (x) is the series. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. This is how generated by usually works in algebra. I know the definition. Generator Math Definition.
From lightofscience1.blogspot.com
Definition of generator, its principle working and its applications For Generator Math Definition A set of generators is a set of group elements such that possibly repeated application of the generators. As an example, remember the dihedral group, the symmetries of an n. A 0, a 1,., a n,. This is how generated by usually works in algebra. A group $g$ is generated by $h\subseteq g$ if you can take the elements. The. Generator Math Definition.
From www.mdpi.com
Mathematics Free FullText TransformerBased Seq2Seq Model for Generator Math Definition A set of generators is a set of group elements such that possibly repeated application of the generators. As an example, remember the dihedral group, the symmetries of an n. This is how generated by usually works in algebra. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with. Generator Math Definition.
From youvegotthismath.com
Free Lines Rays and Line Segments Worksheet 10+ Pages Generator Math Definition A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. A set of generators is a set of group elements such that possibly repeated application of the generators. As an example, remember the dihedral group, the symmetries of an n. A group $g$ is generated by $h\subseteq g$ if you can take the elements. A 0,. Generator Math Definition.
From www.wolframalpha.com
Wolfram Problem Generator Online Practice Questions & Answers Generator Math Definition A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. A group $g$ is generated by $h\subseteq g$ if you can take the elements. Generators are some special elements that we pick out. Generator Math Definition.
From www.chegg.com
Solved A good definition should be Generator Math Definition A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. This is how generated by usually works in algebra. A set of generators is a set of group elements such that possibly repeated application of the generators. Generators are some special elements that we pick out which. Generator Math Definition.
From www.artofit.org
Math worksheet generator Artofit Generator Math Definition A 0, a 1,., a n,. As an example, remember the dihedral group, the symmetries of an n. This is how generated by usually works in algebra. The corresponding generating function f(x) f (x) is the series. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or.. Generator Math Definition.
From eduinput.com
ThreePhase GeneratorDefinition, Working, Connections, And Applications Generator Math Definition A 0, a 1,., a n,. Generators are some special elements that we pick out which can be used to get to any other element in the group. I know the definition of group generators: A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. The definitions. Generator Math Definition.
From gamesmartz.com
Generator Definition & Image GameSmartz Generator Math Definition A 0, a 1,., a n,. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. A set of generators is a set of group elements such that possibly repeated application of the generators. A set of generators $(g_1,.,g_n)$ is a set of group elements such that. Generator Math Definition.
From core-electronics.com.au
Rigol DG1022 vs Siglent SDG1025 vs Siglent SDG1032X Function Generator Math Definition A group $g$ is generated by $h\subseteq g$ if you can take the elements. Generators are some special elements that we pick out which can be used to get to any other element in the group. A 0, a 1,., a n,. A set of generators is a set of group elements such that possibly repeated application of the generators.. Generator Math Definition.
From www.chegg.com
Solved Question 6Under the economist's definition, Generator Math Definition The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. I know the definition of group generators: Generators are some special elements that we pick out which can be used to get to any other element in the group. A unit \(g \in \mathbb{z}_n^*\) is called a. Generator Math Definition.
From giouemqek.blob.core.windows.net
Partitions Math at Eleanor Mcewen blog Generator Math Definition A group $g$ is generated by $h\subseteq g$ if you can take the elements. This is how generated by usually works in algebra. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly.. Generator Math Definition.
From imagetou.com
Lora Stable Diffusion Explained Image to u Generator Math Definition Generators are some special elements that we pick out which can be used to get to any other element in the group. A group $g$ is generated by $h\subseteq g$ if you can take the elements. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. I. Generator Math Definition.
From www.chegg.com
Solved ach definition to the appropriate muscle Generator Math Definition As an example, remember the dihedral group, the symmetries of an n. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. A set of generators is a set of group elements such that possibly repeated application of the generators. The corresponding generating function f(x) f (x). Generator Math Definition.
From www.youtube.com
Finite Math Markov Transition Diagram to Matrix Practice YouTube Generator Math Definition The corresponding generating function f(x) f (x) is the series. This is how generated by usually works in algebra. A set of generators is a set of group elements such that possibly repeated application of the generators. I know the definition of group generators: A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. A 0,. Generator Math Definition.
From www.worksheetsplanet.com
What is a Constant Definition of Constant Generator Math Definition A set of generators is a set of group elements such that possibly repeated application of the generators. A group $g$ is generated by $h\subseteq g$ if you can take the elements. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. I know the definition of group generators: A unit \(g \in \mathbb{z}_n^*\) is called. Generator Math Definition.
From www.youtube.com
GENERATOR GENERATING ELEMENT GROUP THEORY ALGEBRAIC STRUCTURES Generator Math Definition As an example, remember the dihedral group, the symmetries of an n. I know the definition of group generators: A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. The corresponding generating function f(x) f (x) is the series. Generators are some special elements that we pick. Generator Math Definition.
From play.google.com
Math Generator Android Apps on Google Play Generator Math Definition I know the definition of group generators: The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. This is how generated by usually works in algebra. A set of generators is a set of group elements such that possibly repeated application of the generators. A unit \(g. Generator Math Definition.
From forum.arduino.cc
AD9833 function generator Project Guidance Arduino Forum Generator Math Definition Generators are some special elements that we pick out which can be used to get to any other element in the group. A set of generators is a set of group elements such that possibly repeated application of the generators. The corresponding generating function f(x) f (x) is the series. I know the definition of group generators: A group $g$. Generator Math Definition.
From classfullsubchelate.z13.web.core.windows.net
Matching Definition Worksheet Generator Generator Math Definition The corresponding generating function f(x) f (x) is the series. I know the definition of group generators: A set of generators is a set of group elements such that possibly repeated application of the generators. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. This is. Generator Math Definition.
From www.chegg.com
Solved cc Match the term with its definition or Generator Math Definition The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. Generators are some special elements that we pick out which can be used to get to any other element in the group. The. Generator Math Definition.
From netgroup.edu.vn
Update more than 141 definition of ring in algebra best netgroup.edu.vn Generator Math Definition Generators are some special elements that we pick out which can be used to get to any other element in the group. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for every \(a \in \mathbb{z}_n^*\) we have \(g^k. I know the definition of group generators: A 0, a 1,., a n,. A set. Generator Math Definition.
From www.youtube.com
(Abstract Algebra 1) Definition of a Cyclic Group YouTube Generator Math Definition I know the definition of group generators: A set of generators $(g_1,.,g_n)$ is a set of group elements such that possibly. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. A unit \(g \in \mathbb{z}_n^*\) is called a generator or primitive root of \(\mathbb{z}_n^*\) if for. Generator Math Definition.
From download-ats.com
Definition Generator v1.0 By Rushour109 (1.47.x) for ATS Generator Math Definition A 0, a 1,., a n,. The definitions of generating set of a group using finite sums, given above, must be slightly modified when one deals with semigroups or. A set of generators is a set of group elements such that possibly repeated application of the generators. This is how generated by usually works in algebra. A set of generators. Generator Math Definition.
From dizz.com
Types of Generators and their Uses Design Engineering Generator Math Definition This is how generated by usually works in algebra. Generators are some special elements that we pick out which can be used to get to any other element in the group. As an example, remember the dihedral group, the symmetries of an n. The definitions of generating set of a group using finite sums, given above, must be slightly modified. Generator Math Definition.
From worksheetmagicflores123.s3-website-us-east-1.amazonaws.com
Scrambled Math Words Generator Math Definition I know the definition of group generators: A set of generators is a set of group elements such that possibly repeated application of the generators. Generators are some special elements that we pick out which can be used to get to any other element in the group. As an example, remember the dihedral group, the symmetries of an n. A. Generator Math Definition.