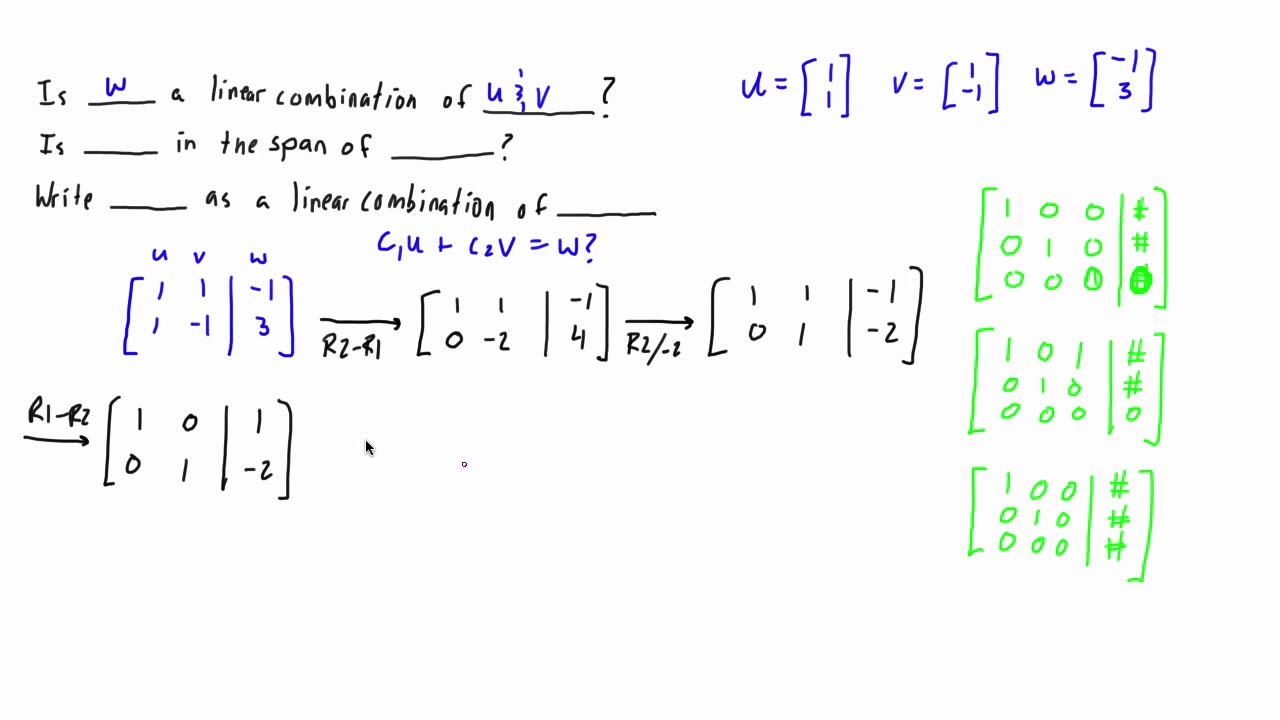Linear Combination Of Basis Vectors . The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: This example demonstrates the connection between linear combinations and linear systems. They are linearly independent, meaning that no vector in. Basis vectors are a set of vectors that span the entire vector space. $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. We write two linear combinations of the four given spanning vectors, chosen at random: Asking if a vector \(\mathbf b\) is a linear combination of vectors.
from www.youtube.com
Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. Basis vectors are a set of vectors that span the entire vector space. This example demonstrates the connection between linear combinations and linear systems. If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). They are linearly independent, meaning that no vector in. $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. Asking if a vector \(\mathbf b\) is a linear combination of vectors. We write two linear combinations of the four given spanning vectors, chosen at random:
How to determine if one vector is a linear combination of a set of vectors YouTube
Linear Combination Of Basis Vectors $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). They are linearly independent, meaning that no vector in. Basis vectors are a set of vectors that span the entire vector space. The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. This example demonstrates the connection between linear combinations and linear systems. Asking if a vector \(\mathbf b\) is a linear combination of vectors. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: We write two linear combinations of the four given spanning vectors, chosen at random:
From www.youtube.com
vector equations linear combinations YouTube Linear Combination Of Basis Vectors They are linearly independent, meaning that no vector in. W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. Asking if a vector \(\mathbf b\) is a linear combination of. Linear Combination Of Basis Vectors.
From www.chegg.com
Solved 7. Write the vector v=⎝⎛512⎠⎞ as a unique linear Linear Combination Of Basis Vectors We write two linear combinations of the four given spanning vectors, chosen at random: Asking if a vector \(\mathbf b\) is a linear combination of vectors. $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the.. Linear Combination Of Basis Vectors.
From www.youtube.com
Proving a Set of Vectors is a Basis Linear Algebra YouTube Linear Combination Of Basis Vectors W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). Asking if a vector \(\mathbf b\) is a linear combination of vectors. The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\}. Linear Combination Of Basis Vectors.
From www.chegg.com
Solved LINEAR COMBINATIONS OF VECTORS IN A VECTOR SPACE Linear Combination Of Basis Vectors We write two linear combinations of the four given spanning vectors, chosen at random: $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: This example demonstrates the connection between linear combinations and linear systems. If we have a (finite) basis for such a vector space v, then, since. Linear Combination Of Basis Vectors.
From www.transtutors.com
(Get Answer) Linear Combinations, Span, And Basis Vectors Linear Combinations,... Transtutors Linear Combination Of Basis Vectors Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: This example demonstrates the connection between linear combinations and linear systems. They are linearly independent, meaning that no vector in. The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is. Linear Combination Of Basis Vectors.
From www.slideserve.com
PPT Chapter Content PowerPoint Presentation, free download ID6335866 Linear Combination Of Basis Vectors $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. They are linearly independent, meaning that no vector in. The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. We write two linear combinations of the four given spanning vectors, chosen at random: This example demonstrates. Linear Combination Of Basis Vectors.
From www.youtube.com
2555 Math 3 lecture 4 Ch 5 3 4 linear combination span, independence basis vectors and dimension Linear Combination Of Basis Vectors Basis vectors are a set of vectors that span the entire vector space. If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. They are linearly independent, meaning that no vector in. Asking. Linear Combination Of Basis Vectors.
From datahacker.rs
007 Linear Algebra Change of basis Master Data Science Linear Combination Of Basis Vectors Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. We write two linear combinations of the four. Linear Combination Of Basis Vectors.
From www.slideserve.com
PPT Linear Algebra Review PowerPoint Presentation, free download ID5486311 Linear Combination Of Basis Vectors The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: This example demonstrates the connection between linear combinations and linear systems. W1 = (1 − 2 2). Linear Combination Of Basis Vectors.
From calculuscoaches.com
forming linear combinations of vectors Calculus Coaches Linear Combination Of Basis Vectors If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. Basis vectors are a set of vectors that span the entire vector space. $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. Asking if a vector. Linear Combination Of Basis Vectors.
From www.youtube.com
Determine if b is a linear combination of vectors formed from the columns of matrix A. b=(2,1,6 Linear Combination Of Basis Vectors They are linearly independent, meaning that no vector in. W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: If we. Linear Combination Of Basis Vectors.
From www.geeksforgeeks.org
Basis Vectors in Linear Algebra ML Linear Combination Of Basis Vectors Asking if a vector \(\mathbf b\) is a linear combination of vectors. Basis vectors are a set of vectors that span the entire vector space. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly. Linear Combination Of Basis Vectors.
From www.youtube.com
How to determine if one vector is a linear combination of a set of vectors YouTube Linear Combination Of Basis Vectors If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4). Linear Combination Of Basis Vectors.
From www.youtube.com
Linear Combination of vectors using i and j YouTube Linear Combination Of Basis Vectors $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. Basis vectors are a set of vectors that span the entire vector space. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: We write two linear combinations of the four given spanning vectors, chosen at random: If we have a (finite) basis for such a vector space v,. Linear Combination Of Basis Vectors.
From www.youtube.com
write u as Linear Combination of vectors Linear Algebra YouTube Linear Combination Of Basis Vectors Basis vectors are a set of vectors that span the entire vector space. W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). Asking if a vector \(\mathbf b\) is a linear combination of vectors. We. Linear Combination Of Basis Vectors.
From datahacker.rs
Linear Algebra Linear combination of Vectors Master Data Science Linear Combination Of Basis Vectors The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. We write two linear combinations of the four given spanning vectors, chosen at random: Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: $u=\begin{pmatrix} 1 \\. Linear Combination Of Basis Vectors.
From www.vrogue.co
Linear Algebra Tutorial Basis Vector vrogue.co Linear Combination Of Basis Vectors Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). Basis vectors are a set of vectors that span the entire. Linear Combination Of Basis Vectors.
From www.slideserve.com
PPT Math Review Week 1, Wed Jan 6 PowerPoint Presentation, free download ID5456177 Linear Combination Of Basis Vectors If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: The easiest way to check whether a given. Linear Combination Of Basis Vectors.
From www.youtube.com
Write a vector as a linear combination of a set of vectors YouTube Linear Combination Of Basis Vectors W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). We write two linear combinations of the four given spanning vectors, chosen at random: They are linearly independent, meaning that no vector in. Asking if a. Linear Combination Of Basis Vectors.
From www.chegg.com
Solved (a) Explain why12 is a basis for IR, and write the Linear Combination Of Basis Vectors If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: The easiest way to check whether a given. Linear Combination Of Basis Vectors.
From www.slideserve.com
PPT VectorValued Functions PowerPoint Presentation ID2465345 Linear Combination Of Basis Vectors Basis vectors are a set of vectors that span the entire vector space. $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0. Linear Combination Of Basis Vectors.
From www.youtube.com
Linear algebra, ch4, part8(4.5 Linear Combination of Vectors) YouTube Linear Combination Of Basis Vectors The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. They are linearly independent, meaning that no vector in. $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. Asking if a vector \(\mathbf b\) is a linear combination of vectors. We write two linear combinations. Linear Combination Of Basis Vectors.
From datahacker.rs
Linear Algebra Linear combination of Vectors Master Data Science Linear Combination Of Basis Vectors The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear. Linear Combination Of Basis Vectors.
From www.chegg.com
Solved 5 We can write the vector V = 4 in the 2 linear Linear Combination Of Basis Vectors We write two linear combinations of the four given spanning vectors, chosen at random: They are linearly independent, meaning that no vector in. The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. This example demonstrates the connection between linear combinations and. Linear Combination Of Basis Vectors.
From hadrienj.github.io
Essential Math for Data Science Basis and Change of Basis Code · Data Science Linear Combination Of Basis Vectors The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. They are linearly independent, meaning that no vector in. Asking if a vector \(\mathbf b\) is a linear combination of vectors. We write two linear combinations of the four given spanning vectors,. Linear Combination Of Basis Vectors.
From www.youtube.com
Linear combinations, span, and basis vectors Chapter 2, Essence of linear algebra YouTube Linear Combination Of Basis Vectors $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. Asking if a vector \(\mathbf b\) is a linear combination of vectors. They are linearly independent, meaning that no vector in. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: Basis vectors are a set of vectors that span the entire vector space. If we have a (finite). Linear Combination Of Basis Vectors.
From www.chegg.com
Solved 4 5 in the linear combination of basis vectors u = We Linear Combination Of Basis Vectors This example demonstrates the connection between linear combinations and linear systems. Basis vectors are a set of vectors that span the entire vector space. Asking if a vector \(\mathbf b\) is a linear combination of vectors. W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) +. Linear Combination Of Basis Vectors.
From www.youtube.com
Linear Algebra 42, Linear Combination of Vectors, Orthogonal Vectors YouTube Linear Combination Of Basis Vectors The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear. Linear Combination Of Basis Vectors.
From www.youtube.com
Linear Algebra Is a vector linear combination of other vectors? An example. YouTube Linear Combination Of Basis Vectors This example demonstrates the connection between linear combinations and linear systems. They are linearly independent, meaning that no vector in. The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of. Linear Combination Of Basis Vectors.
From www.youtube.com
Linear Combination of Vectors YouTube Linear Combination Of Basis Vectors W1 = (1 − 2 2) + (2 − 3 4) = (3 − 5 6) w2 = − (2 − 3 4) + 1 2(0 4 0) = (− 2 5 − 4). Basis vectors are a set of vectors that span the entire vector space. Asking if a vector \(\mathbf b\) is a linear combination of vectors. If. Linear Combination Of Basis Vectors.
From www.geogebra.org
Basis Vectors, Linear Combinations, Span and Linear Independence/Dependence GeoGebra Linear Combination Of Basis Vectors This example demonstrates the connection between linear combinations and linear systems. $u=\begin{pmatrix} 1 \\ 2 \\5 \end{pmatrix}$,. Basis vectors are a set of vectors that span the entire vector space. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: We write two linear combinations of the four given spanning vectors, chosen at random: W1. Linear Combination Of Basis Vectors.
From www.youtube.com
Labtube(Linear Algebra I) Linear Combinations of Vectors YouTube Linear Combination Of Basis Vectors The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. This example demonstrates the connection between linear combinations and linear systems. If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v. Linear Combination Of Basis Vectors.
From calcworkshop.com
Basis of Vector Spaces (A Linear Algebra Guide) Linear Combination Of Basis Vectors If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. Write $\begin{pmatrix} 5 \\ 3 \\15 \end{pmatrix}$ as a linerar combination of the following vectors: Basis vectors are a set of vectors that. Linear Combination Of Basis Vectors.
From www.youtube.com
Linear Algebra Example Problems Vector Space Basis Example 2 YouTube Linear Combination Of Basis Vectors The easiest way to check whether a given set $\ { (a,b,c), (d,e,f), (p,q,r)\} $ of three vectors are linearly independent in $\bbb r^3$ is to find the. If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear. Linear Combination Of Basis Vectors.
From www.youtube.com
Basis of a Vector Space Linear Algebra Sec. 4.5 Part 1 YouTube Linear Combination Of Basis Vectors If we have a (finite) basis for such a vector space v, then, since the vectors in a basis span v , any vector in v can be expressed as a linear combination of the basis vectors. We write two linear combinations of the four given spanning vectors, chosen at random: They are linearly independent, meaning that no vector in.. Linear Combination Of Basis Vectors.