Pedal Triangle Definition . the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. trigonometry/circles and triangles/the pedal triangle. Here is an example of. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections of a \(p\) to the sides of the triangle. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. Given any triangle abc, let the altitudes through each. Let $\triangle abc$ be a triangle. sides and area of pedal triangle. Let $p$ be a point in the plane of. definition pedal triangle of point with respect to triangle.
from demonstrations.wolfram.com
Here is an example of. the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. Given any triangle abc, let the altitudes through each. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections of a \(p\) to the sides of the triangle. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. sides and area of pedal triangle. trigonometry/circles and triangles/the pedal triangle. definition pedal triangle of point with respect to triangle. Let $p$ be a point in the plane of. Let $\triangle abc$ be a triangle.
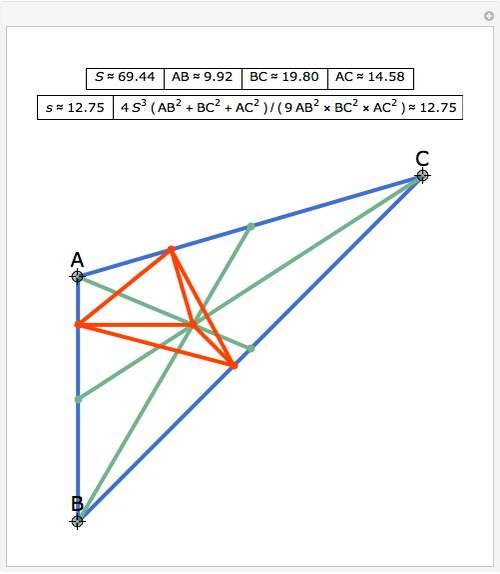
The Area of the Pedal Triangle of the Centroid Wolfram Demonstrations Project
Pedal Triangle Definition Let $p$ be a point in the plane of. Let $p$ be a point in the plane of. Given any triangle abc, let the altitudes through each. Here is an example of. the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. Let $\triangle abc$ be a triangle. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. trigonometry/circles and triangles/the pedal triangle. definition pedal triangle of point with respect to triangle. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections of a \(p\) to the sides of the triangle. sides and area of pedal triangle. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle.
From jwilson.coe.uga.edu
Pedal Triangles Pedal Triangle Definition the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections of a \(p\) to the sides of the triangle. Here is an example of. Given any triangle abc, let the altitudes through each. sides and area of pedal triangle. Pedal triangle of point p with respect to a given δabc. Pedal Triangle Definition.
From brilliant.org
Pedal Triangle Brilliant Math & Science Wiki Pedal Triangle Definition sides and area of pedal triangle. Here is an example of. trigonometry/circles and triangles/the pedal triangle. Let $p$ be a point in the plane of. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. a pedal triangle is. Pedal Triangle Definition.
From www.youtube.com
GEOMETRY 23 Pedal Triangle and its properties YouTube Pedal Triangle Definition sides and area of pedal triangle. Here is an example of. Let $\triangle abc$ be a triangle. definition pedal triangle of point with respect to triangle. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. Pedal triangle of point p with respect. Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal Triangles Pedal Triangle Definition Let $\triangle abc$ be a triangle. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections of a \(p\) to the sides of. Pedal Triangle Definition.
From demonstrations.wolfram.com
The Third Pedal Triangle of a Triangle Wolfram Demonstrations Project Pedal Triangle Definition given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. definition pedal triangle of point with respect to triangle. Here is an example of. a pedal triangle is created by the intersections of perpendicular lines from a point in the. Pedal Triangle Definition.
From www.youtube.com
Property 3 of Pedal Triangle Area of Pedal Triangle YouTube Pedal Triangle Definition the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. Let $\triangle abc$ be a triangle. trigonometry/circles and triangles/the pedal triangle. Here is an example of. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from. Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal Pedal Pedal Triangles Pedal Triangle Definition trigonometry/circles and triangles/the pedal triangle. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. sides and area of pedal triangle. Let $p$ be a point in the plane of. definition pedal triangle of point with respect to triangle. a pedal. Pedal Triangle Definition.
From demonstrations.wolfram.com
Exact Trilinear Coordinates and the Pedal Triangle Wolfram Demonstrations Project Pedal Triangle Definition Here is an example of. Let $\triangle abc$ be a triangle. sides and area of pedal triangle. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. a pedal triangle is created by the intersections of perpendicular lines from a. Pedal Triangle Definition.
From imgbin.com
Pedal Triangle Point Fotpunkt PNG, Clipart, Angle, Area, Art, Circle, Definition Free PNG Download Pedal Triangle Definition sides and area of pedal triangle. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. trigonometry/circles and triangles/the pedal. Pedal Triangle Definition.
From demonstrations.wolfram.com
The Third Pedal Triangle of a Triangle Wolfram Demonstrations Project Pedal Triangle Definition a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. definition pedal triangle of point with respect to triangle. Given any. Pedal Triangle Definition.
From in.pinterest.com
The Pedal Triangle Properties of the triangle Math vocabulary, Geometry formulas, Math formulas Pedal Triangle Definition the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. Given any triangle abc, let the altitudes through each. trigonometry/circles and triangles/the pedal triangle. Let $p$ be a point in the plane of. Here is an example of. given a point p, the pedal triangle. Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal Triangles Pedal Triangle Definition definition pedal triangle of point with respect to triangle. Given any triangle abc, let the altitudes through each. sides and area of pedal triangle. the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. the pedal triangle of a triangle \(abc\) and point \(p\). Pedal Triangle Definition.
From demonstrations.wolfram.com
Euler's Theorem for Pedal Triangles Wolfram Demonstrations Project Pedal Triangle Definition Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. sides and area of pedal triangle. Given any triangle. Pedal Triangle Definition.
From www.researchgate.net
Area of the Pedal Triangle, and the circle whose equation is obtained... Download Scientific Pedal Triangle Definition trigonometry/circles and triangles/the pedal triangle. the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. the pedal triangle of a. Pedal Triangle Definition.
From www.pinterest.com
Pedal triangle and the Orthic triangle in 2022 Geometry high school, Math projects, Geometry Pedal Triangle Definition given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. definition pedal triangle of point with respect to triangle. Let $p$ be a point in the plane of. Here is an example of. the pedal triangle of a triangle \(abc\). Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal triangles Pedal Triangle Definition Let $\triangle abc$ be a triangle. definition pedal triangle of point with respect to triangle. the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p. Pedal Triangle Definition.
From www.youtube.com
Property 2 of Pedal Triangle Length of sides of Pedal Triangle YouTube Pedal Triangle Definition trigonometry/circles and triangles/the pedal triangle. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. Here is an example of. definition pedal triangle of point with respect to triangle. the triangle defined by those three points is the pedal triangle of triangle. Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal Pedal Pedal Triangles Pedal Triangle Definition trigonometry/circles and triangles/the pedal triangle. sides and area of pedal triangle. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars. Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal Triangles Pedal Triangle Definition Let $p$ be a point in the plane of. sides and area of pedal triangle. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices. Pedal Triangle Definition.
From www.geogebra.org
Pedal Triangle GeoGebra Pedal Triangle Definition Let $\triangle abc$ be a triangle. sides and area of pedal triangle. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. definition pedal triangle of point with respect to triangle. given a point p, the pedal triangle of p is the. Pedal Triangle Definition.
From www.youtube.com
Property 1 of Pedal Triangle Angle in a Pedal Triangle YouTube Pedal Triangle Definition Let $p$ be a point in the plane of. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. sides and area of pedal triangle. Given any triangle abc, let the altitudes through each. given a point p, the pedal triangle of p. Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal Triangles EMAT 6680 Pedal Triangle Definition sides and area of pedal triangle. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections of a \(p\) to the sides of the triangle. Here is an example of. Given any triangle abc, let the altitudes through each. Pedal triangle of point p with respect to a given δabc. Pedal Triangle Definition.
From math.stackexchange.com
Angles of a pedal triangle Mathematics Stack Exchange Pedal Triangle Definition Given any triangle abc, let the altitudes through each. the triangle defined by those three points is the pedal triangle of triangle abc, and the point p is called pedal point. Let $p$ be a point in the plane of. Here is an example of. Let $\triangle abc$ be a triangle. the pedal triangle of a triangle \(abc\). Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal Triangles Pedal Triangle Definition trigonometry/circles and triangles/the pedal triangle. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. . Pedal Triangle Definition.
From in.pinterest.com
The Pedal triangle The Orthic triangle Triangle, 2d geometry, Theorems Pedal Triangle Definition definition pedal triangle of point with respect to triangle. Let $\triangle abc$ be a triangle. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections. Pedal Triangle Definition.
From imgbin.com
Pedal Triangle Point Fotpunkt PNG, Clipart, Angle, Area, Art, Circle, Definition Free PNG Download Pedal Triangle Definition Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. Let $p$ be a point in the plane of. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. . Pedal Triangle Definition.
From logicxonomy.com
Pedal Triangle Properties (Powerful Geometry Cheatsheet 2022) Logicxonomy Pedal Triangle Definition definition pedal triangle of point with respect to triangle. Let $\triangle abc$ be a triangle. trigonometry/circles and triangles/the pedal triangle. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. Here is an example of. sides and area of. Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal Triangles Pedal Triangle Definition definition pedal triangle of point with respect to triangle. Let $\triangle abc$ be a triangle. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections of a \(p\) to the sides of the triangle. trigonometry/circles and triangles/the pedal triangle. Here is an example of. Given any triangle abc, let. Pedal Triangle Definition.
From www.youtube.com
What is pedal triangle In acute angle triangle (orthocenter of ABC is Incenter of Pedal Triang Pedal Triangle Definition a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. definition pedal triangle of point with respect to triangle. Here is an example of. Let $p$ be a point in the plane of. the triangle defined by those three points is the pedal. Pedal Triangle Definition.
From www.youtube.com
BASIC OF PEDAL TRIANGLE YouTube Pedal Triangle Definition the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections of a \(p\) to the sides of the triangle. Let $p$ be a point in the plane of. Let $\triangle abc$ be a triangle. given a point p, the pedal triangle of p is the triangle whose polygon vertices are. Pedal Triangle Definition.
From www.pinterest.com
Subjects Pedal Triangle Definition Let $p$ be a point in the plane of. Given any triangle abc, let the altitudes through each. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. definition pedal triangle of point with respect to triangle. given a point p, the pedal. Pedal Triangle Definition.
From in.pinterest.com
Perimeter of the Orthic triangle Pedal triangle Math geometry, Math formulas, Math Pedal Triangle Definition Here is an example of. a pedal triangle is created by the intersections of perpendicular lines from a point in the plane to the sides of a given triangle. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. Let $\triangle abc$ be a. Pedal Triangle Definition.
From demonstrations.wolfram.com
The Area of the Pedal Triangle of the Centroid Wolfram Demonstrations Project Pedal Triangle Definition Here is an example of. Given any triangle abc, let the altitudes through each. definition pedal triangle of point with respect to triangle. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle whose vertices are the projections of a \(p\) to the sides of the triangle. the triangle defined by those three points. Pedal Triangle Definition.
From jwilson.coe.uga.edu
Pedal Triangles Pedal Triangle Definition Here is an example of. Given any triangle abc, let the altitudes through each. sides and area of pedal triangle. Pedal triangle of point p with respect to a given δabc is formed by the feet of the perpendiculars from p to the sides of. the pedal triangle of a triangle \(abc\) and point \(p\) is the triangle. Pedal Triangle Definition.
From e-mathe.blogspot.com
IITJEE ADVANCED MATHS pedal triangle Pedal Triangle Definition Let $p$ be a point in the plane of. Here is an example of. given a point p, the pedal triangle of p is the triangle whose polygon vertices are the feet of the perpendiculars from p to the side lines. sides and area of pedal triangle. Given any triangle abc, let the altitudes through each. Pedal triangle. Pedal Triangle Definition.