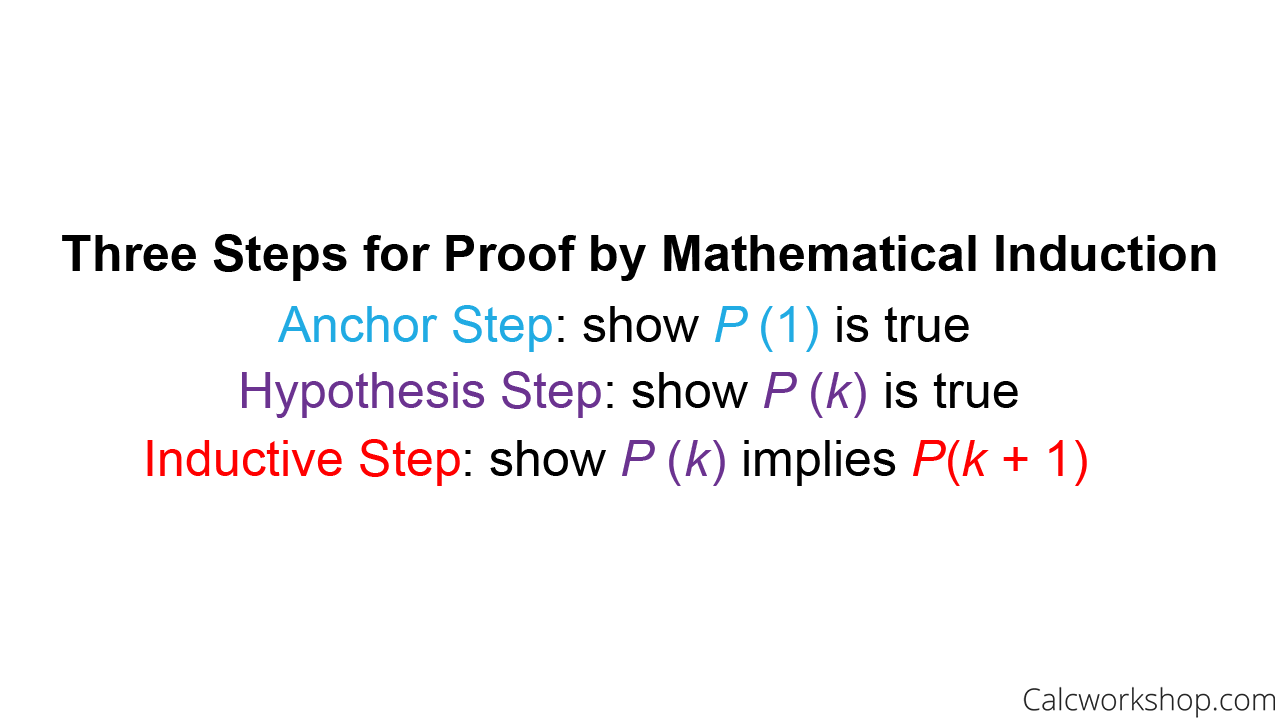
Induction Math Proof at Tristan Enderby blog

Induction Math Proof. Here is a typical example of such an identity: Let’s look at a few examples of proof by induction. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. Mathematical induction (or weak mathematical induction) is a method to prove or establish mathematical statements,. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. In this section, we will learn a. One of the most fundamental sets in mathematics is the set of natural numbers \ (\mathbb {n}\). For example, when we predict a nth term for a given sequence of numbers, mathematics induction is useful to prove the. In these examples, we will structure our proofs explicitly to label the base case, inductive. 1 + 2 + 3 + ⋯. This step can be one of the.

Mathematical induction (or weak mathematical induction) is a method to prove or establish mathematical statements,. For example, when we predict a nth term for a given sequence of numbers, mathematics induction is useful to prove the. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. One of the most fundamental sets in mathematics is the set of natural numbers \ (\mathbb {n}\). Here is a typical example of such an identity: This step can be one of the. In these examples, we will structure our proofs explicitly to label the base case, inductive. Let’s look at a few examples of proof by induction. 1 + 2 + 3 + ⋯. In this section, we will learn a.

Principle of Mathematical Induction (5 Amazing Examples!)

Induction Math Proof 1 + 2 + 3 + ⋯. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. For example, when we predict a nth term for a given sequence of numbers, mathematics induction is useful to prove the. In this section, we will learn a. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. One of the most fundamental sets in mathematics is the set of natural numbers \ (\mathbb {n}\). 1 + 2 + 3 + ⋯. Let’s look at a few examples of proof by induction. This step can be one of the. Mathematical induction (or weak mathematical induction) is a method to prove or establish mathematical statements,. Here is a typical example of such an identity: In these examples, we will structure our proofs explicitly to label the base case, inductive.