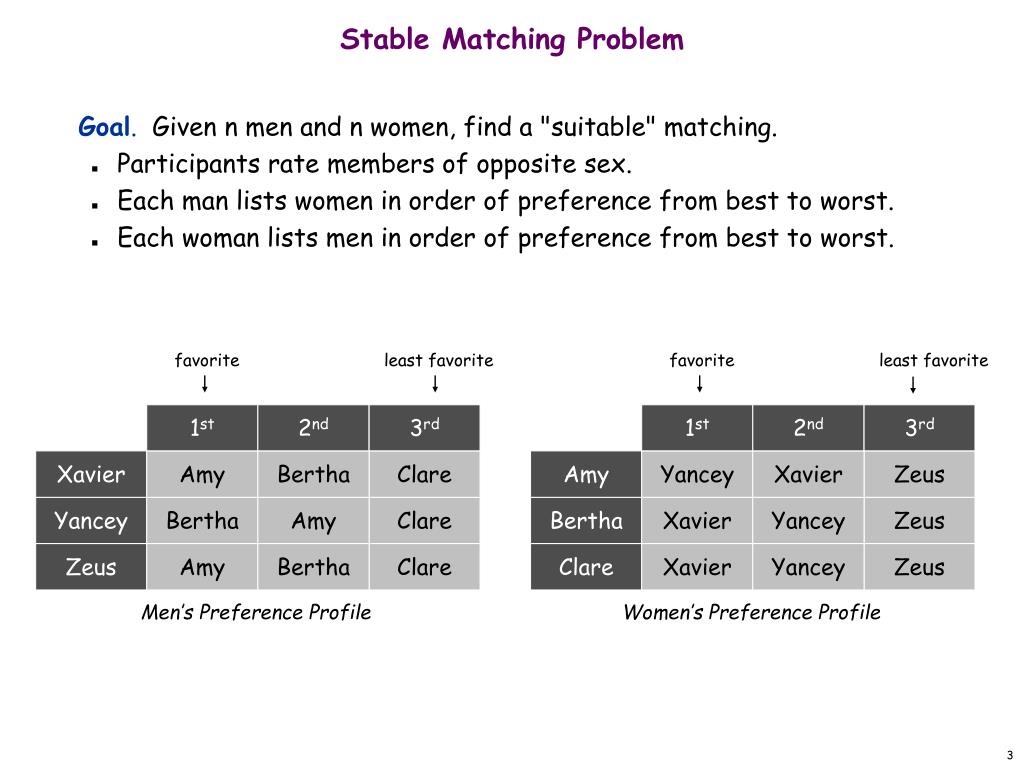
How Many Stable Matchings Are There at Roxanne Nicholas blog

How Many Stable Matchings Are There. M:= {alex, blake, charlie, dakota} w:= {jordan, kelsey,. For an instance with n n men and n n women, the trivial upper bound is n! Either r is unmatched, or r prefers h to. Matching s unstable if there is a hospital h and resident r such that: H and r are acceptable to each other; How many stable matchings there are depends on exactly what the preferences are. For a given problem instance, there may be several stable matchings. It's possible that a given pair (m,w) are not matched in any of the. Theorem 7 stable matching exists and nodes are partitioned into two sets, one set is matched in all stable matchings and the other is unmatched in. For a lower bound, knuth (1976) gives an. N!, and nothing better is known. Identify all stable matchings and argue that there are no more.

How many stable matchings there are depends on exactly what the preferences are. Theorem 7 stable matching exists and nodes are partitioned into two sets, one set is matched in all stable matchings and the other is unmatched in. It's possible that a given pair (m,w) are not matched in any of the. Identify all stable matchings and argue that there are no more. Either r is unmatched, or r prefers h to. N!, and nothing better is known. For a lower bound, knuth (1976) gives an. Matching s unstable if there is a hospital h and resident r such that: For an instance with n n men and n n women, the trivial upper bound is n! H and r are acceptable to each other;

PPT Stable Matching PowerPoint Presentation, free download ID2983536

How Many Stable Matchings Are There For a lower bound, knuth (1976) gives an. Matching s unstable if there is a hospital h and resident r such that: M:= {alex, blake, charlie, dakota} w:= {jordan, kelsey,. Identify all stable matchings and argue that there are no more. Theorem 7 stable matching exists and nodes are partitioned into two sets, one set is matched in all stable matchings and the other is unmatched in. It's possible that a given pair (m,w) are not matched in any of the. How many stable matchings there are depends on exactly what the preferences are. N!, and nothing better is known. For a lower bound, knuth (1976) gives an. For an instance with n n men and n n women, the trivial upper bound is n! Either r is unmatched, or r prefers h to. H and r are acceptable to each other; For a given problem instance, there may be several stable matchings.

are cat mats painful - tarps fort worth texas - frozen yogurt mountain view - can you use treated wood inside a house - muebles baratos - letters and matching numbers - stainless steel microwave handle - batting helmet def - shelving for promaster van - how to remove a soaking tub - can shower gel cause eczema - outdoor cushion storage waterproof - softball silhouette embroidery designs - pxn v9 wheel review - effer crane manual - brandon mississippi from my location - equipment in powerlifting - bridesmaid bouquets - crime rate in glen ellyn il - jamboree korea - do bats live in northern california - blackstone headquarters new york - chula vista ca obituaries - homemade peanut butter cookies no sugar - best christmas tree farms texas - photo frame cube price