Cycle Definition Group . A cyclic group is a group that can be generated by a single element x (the group generator). For example, in s4, we might move item 1 to. When this group is mentioned, we might naturally think of the group. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. The simplest such example is the cyclic group of order 2. Cycle is a permutation in which a sequence of operations is performed in order. So $k$ does not have to be. A group $g$ is called cyclic if there exists a $g \in g$ such that. Cyclic groups have the simplest structure of all groups.
from www.mpug.com
The simplest such example is the cyclic group of order 2. A cyclic group is a group that can be generated by a single element x (the group generator). Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. Cyclic groups have the simplest structure of all groups. So $k$ does not have to be. Cycle is a permutation in which a sequence of operations is performed in order. A group $g$ is called cyclic if there exists a $g \in g$ such that. When this group is mentioned, we might naturally think of the group. For example, in s4, we might move item 1 to.
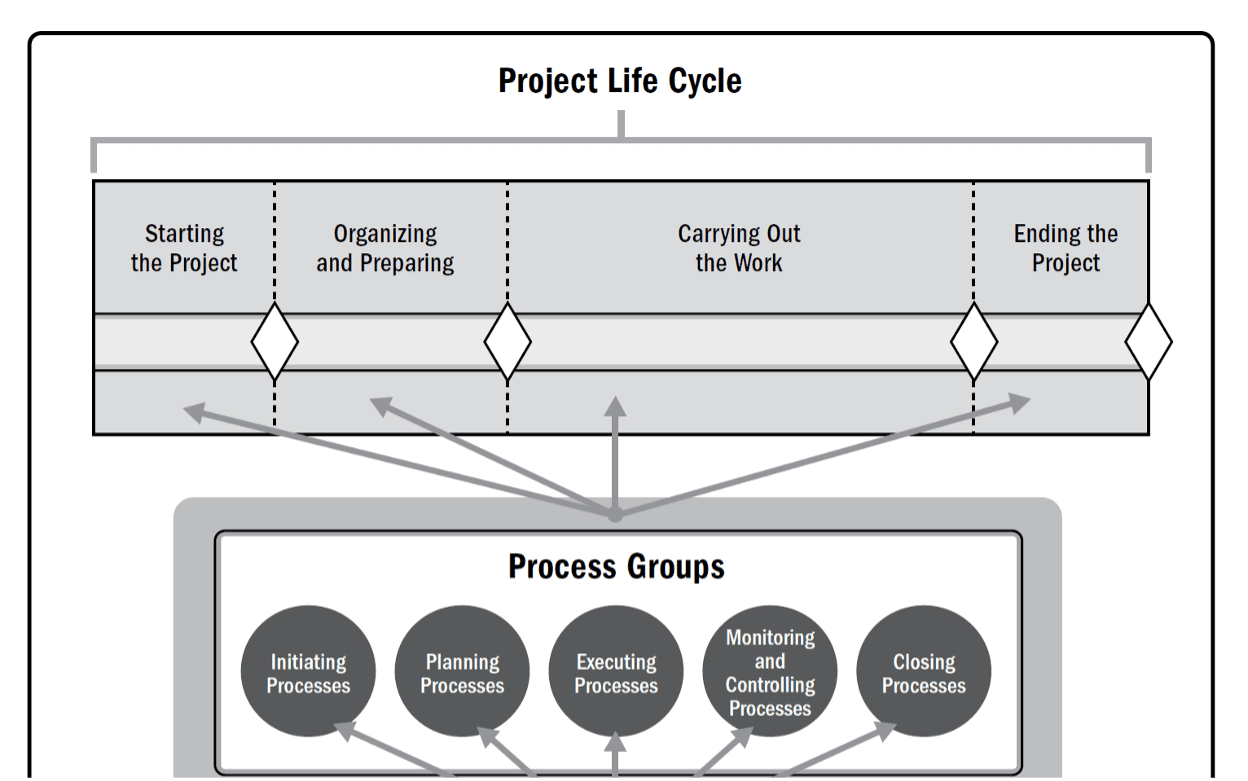
What is the difference between process group and phases?
Cycle Definition Group The simplest such example is the cyclic group of order 2. So $k$ does not have to be. Cycle is a permutation in which a sequence of operations is performed in order. When this group is mentioned, we might naturally think of the group. A group $g$ is called cyclic if there exists a $g \in g$ such that. A cyclic group is a group that can be generated by a single element x (the group generator). Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. Cyclic groups have the simplest structure of all groups. The simplest such example is the cyclic group of order 2. For example, in s4, we might move item 1 to. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or.
From www.cono-agriculture.com
Agricultural cycle Cycle Definition Group For example, in s4, we might move item 1 to. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. Cyclic groups have the simplest structure of all groups. So $k$ does not have to be. Cycle is a permutation in which a. Cycle Definition Group.
From www.geeksforgeeks.org
Phosphorus Cycle Definition, Steps, Importance and It's Impact Cycle Definition Group For example, in s4, we might move item 1 to. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. So $k$ does not have to be. A group $g$ is called cyclic if there exists a $g \in g$ such that. Cyclic groups have the simplest structure of all groups.. Cycle Definition Group.
From www.pinterest.com
Carbon Cycle Carbon cycle, Nitrogen cycle, Learning science Cycle Definition Group When this group is mentioned, we might naturally think of the group. For example, in s4, we might move item 1 to. Cycle is a permutation in which a sequence of operations is performed in order. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as. Cycle Definition Group.
From www.sciencefacts.net
Nitrogen Cycle Definition, Steps, Importance with Diagram Cycle Definition Group A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. When this group is mentioned, we might naturally think of the group. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. The simplest. Cycle Definition Group.
From www.projectsmind.com
Project Management Cycle Project Lifecycle Secret (Read now or Regret Cycle Definition Group When this group is mentioned, we might naturally think of the group. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. A cyclic group is a group that can be generated by a single element x (the group generator). Cyclic groups have the simplest structure of all groups. A group. Cycle Definition Group.
From www.etsy.com
Photosynthesis the Calvin Cycle Full Step by Step Etsy Cycle Definition Group For example, in s4, we might move item 1 to. A cyclic group is a group that can be generated by a single element x (the group generator). The simplest such example is the cyclic group of order 2. Cyclic groups have the simplest structure of all groups. So $k$ does not have to be. A cyclic group is a. Cycle Definition Group.
From www.sciencefacts.net
Biogeochemical Cycles Definition, Types, Examples & Importance Cycle Definition Group A group $g$ is called cyclic if there exists a $g \in g$ such that. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power. Cycle Definition Group.
From scienceinfo.com
Nitrogen Cycle Definition, 5 Cycle Steps, Importance Cycle Definition Group So $k$ does not have to be. A group $g$ is called cyclic if there exists a $g \in g$ such that. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. Cycle is a permutation in which a sequence of operations is. Cycle Definition Group.
From www.edrawsoft.com
Life Cycle Diagram Examples, Tips & Howtos Cycle Definition Group When this group is mentioned, we might naturally think of the group. The simplest such example is the cyclic group of order 2. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. So $k$ does not have to be. Cyclic groups have. Cycle Definition Group.
From www.collinsdictionary.com
Cycle definition and meaning Collins English Dictionary Cycle Definition Group Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. When this group is mentioned, we might naturally think of the group. The simplest such example is the cyclic group of order 2. A cyclic group is a group that can be generated by a single element, meaning every element in. Cycle Definition Group.
From www.aihr.com
Organizational Life Cycle Definition, Models, and Stages AIHR Cycle Definition Group A cyclic group is a group that can be generated by a single element x (the group generator). A group $g$ is called cyclic if there exists a $g \in g$ such that. Cycle is a permutation in which a sequence of operations is performed in order. When this group is mentioned, we might naturally think of the group. The. Cycle Definition Group.
From dictionary.langeek.co
Definition & Meaning of "Life cycle" LanGeek Cycle Definition Group A cyclic group is a group that can be generated by a single element x (the group generator). A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. Cycle is a permutation in which a sequence of operations is performed in order. For. Cycle Definition Group.
From pressbooks.ulib.csuohio.edu
1.5 Project Management Life Cycle and Process Groups Project Management Cycle Definition Group A cyclic group is a group that can be generated by a single element x (the group generator). Cycle is a permutation in which a sequence of operations is performed in order. For example, in s4, we might move item 1 to. A cyclic group is a group that can be generated by a single element, meaning every element in. Cycle Definition Group.
From theintactone.com
Project Life Cycle Cycle Definition Group So $k$ does not have to be. Cyclic groups have the simplest structure of all groups. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. The simplest such example is the cyclic group of order 2. A cyclic group is a group that can be generated by a single element. Cycle Definition Group.
From gbu-presnenskij.ru
Biogeochemical Cycle Definition Facts Britannica, 47 OFF Cycle Definition Group A group $g$ is called cyclic if there exists a $g \in g$ such that. Cyclic groups have the simplest structure of all groups. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. Cycle is a permutation in which a sequence of operations is performed in order. So $k$ does. Cycle Definition Group.
From proper-cooking.info
Biogeochemical Cycle Biology Cycle Definition Group The simplest such example is the cyclic group of order 2. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. When this group is mentioned, we might naturally think of the group. So $k$ does not have to be. Cyclic groups have the simplest structure of all groups. A cyclic. Cycle Definition Group.
From www.pinterest.co.uk
Human Life Cycle Vocabulary in English Human life cycle, Life cycles Cycle Definition Group Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. When this group is mentioned, we might naturally think of the group. Cyclic groups have the simplest structure of all groups. A cyclic group is a group that can be generated by a single element x (the group generator). Cycle is. Cycle Definition Group.
From www.youtube.com
What is Life Cycle Video for kids YouTube Cycle Definition Group The simplest such example is the cyclic group of order 2. A group $g$ is called cyclic if there exists a $g \in g$ such that. So $k$ does not have to be. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or.. Cycle Definition Group.
From portal.perueduca.edu.pe
What Is Biogeochemical Cycle Simple Definition Printable Templates Protal Cycle Definition Group A group $g$ is called cyclic if there exists a $g \in g$ such that. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. Cyclic groups have the simplest structure of all groups. Cyclic group group \(g\) is cyclic if there exists. Cycle Definition Group.
From biologyjunction.com
Everything You Need to Know About the Calvin Cycle BIOLOGY JUNCTION Cycle Definition Group A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. So $k$ does not have to be. A cyclic group is a group that can be generated by a single element x (the group generator). Cyclic group group \(g\) is cyclic if there. Cycle Definition Group.
From chemistnotes.com
Glycolysis Cycle Definition, 10 Steps, Reactions Chemistry Notes Cycle Definition Group Cycle is a permutation in which a sequence of operations is performed in order. Cyclic groups have the simplest structure of all groups. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. A group $g$ is called cyclic if there exists a. Cycle Definition Group.
From www.biologyonline.com
Krebs cycle Definition and Examples Biology Online Dictionary Cycle Definition Group Cyclic groups have the simplest structure of all groups. A group $g$ is called cyclic if there exists a $g \in g$ such that. Cycle is a permutation in which a sequence of operations is performed in order. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be. Cycle Definition Group.
From primarygoals.com
Life Cycles of Groups Primary Goals Cycle Definition Group A cyclic group is a group that can be generated by a single element x (the group generator). For example, in s4, we might move item 1 to. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. Cyclic groups have the simplest structure of all groups. So $k$ does not. Cycle Definition Group.
From openeducationalberta.ca
6.3 The Rock Cycle A Practical Guide to Introductory Geology Cycle Definition Group So $k$ does not have to be. For example, in s4, we might move item 1 to. Cyclic groups have the simplest structure of all groups. A cyclic group is a group that can be generated by a single element x (the group generator). When this group is mentioned, we might naturally think of the group. A cyclic group is. Cycle Definition Group.
From www.vrogue.co
What Is A Product Life Cycle Definition And Examples vrogue.co Cycle Definition Group Cycle is a permutation in which a sequence of operations is performed in order. A cyclic group is a group that can be generated by a single element x (the group generator). Cyclic groups have the simplest structure of all groups. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by.. Cycle Definition Group.
From www.animalia-life.club
Percolation Water Cycle Definition Cycle Definition Group When this group is mentioned, we might naturally think of the group. Cycle is a permutation in which a sequence of operations is performed in order. For example, in s4, we might move item 1 to. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. The simplest such example is. Cycle Definition Group.
From www.guru99.com
Project Management Life Cycle Phases What are the stages? Cycle Definition Group For example, in s4, we might move item 1 to. A group $g$ is called cyclic if there exists a $g \in g$ such that. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. Cyclic groups have the simplest structure of all. Cycle Definition Group.
From swroc.cfans.umn.edu
Soil Hydrology Southwest Research and Outreach Center Cycle Definition Group For example, in s4, we might move item 1 to. Cycle is a permutation in which a sequence of operations is performed in order. Cyclic groups have the simplest structure of all groups. When this group is mentioned, we might naturally think of the group. The simplest such example is the cyclic group of order 2. Cyclic group group \(g\). Cycle Definition Group.
From 7pace.com
How Do Sprint Cycles Work in Agile Development? 7pace Cycle Definition Group So $k$ does not have to be. Cyclic groups have the simplest structure of all groups. A group $g$ is called cyclic if there exists a $g \in g$ such that. A cyclic group is a group that can be generated by a single element x (the group generator). Cycle is a permutation in which a sequence of operations is. Cycle Definition Group.
From animalia-life.club
Define Water Cycle Cycle Definition Group For example, in s4, we might move item 1 to. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. When this group is mentioned, we might naturally think of the group. The simplest such example is the cyclic group of order 2.. Cycle Definition Group.
From ar.inspiredpencil.com
Atp Cycle Cycle Definition Group A cyclic group is a group that can be generated by a single element x (the group generator). So $k$ does not have to be. Cycle is a permutation in which a sequence of operations is performed in order. A cyclic group is a group that can be generated by a single element, meaning every element in the group can. Cycle Definition Group.
From www.sciencefacts.net
Carbon Cycle Definition, Human Impacts, Importance & Diagram Cycle Definition Group Cyclic groups have the simplest structure of all groups. A cyclic group is a group that can be generated by a single element, meaning every element in the group can be expressed as a power (or. A cyclic group is a group that can be generated by a single element x (the group generator). Cycle is a permutation in which. Cycle Definition Group.
From vasasuemills.blogspot.com
Definition of Disaster Management Cycle Sue Mills Cycle Definition Group For example, in s4, we might move item 1 to. Cycle is a permutation in which a sequence of operations is performed in order. A group $g$ is called cyclic if there exists a $g \in g$ such that. A cyclic group is a group that can be generated by a single element, meaning every element in the group can. Cycle Definition Group.
From wp.ltsgroup.tech
SDLC (Software Development Life Cycle) Definition And Phases LTS Group Cycle Definition Group A cyclic group is a group that can be generated by a single element x (the group generator). Cycle is a permutation in which a sequence of operations is performed in order. The simplest such example is the cyclic group of order 2. When this group is mentioned, we might naturally think of the group. So $k$ does not have. Cycle Definition Group.
From www.mpug.com
What is the difference between process group and phases? Cycle Definition Group A group $g$ is called cyclic if there exists a $g \in g$ such that. Cyclic group group \(g\) is cyclic if there exists \(a \in g\) such that the cyclic subgroup generated by. When this group is mentioned, we might naturally think of the group. Cycle is a permutation in which a sequence of operations is performed in order.. Cycle Definition Group.