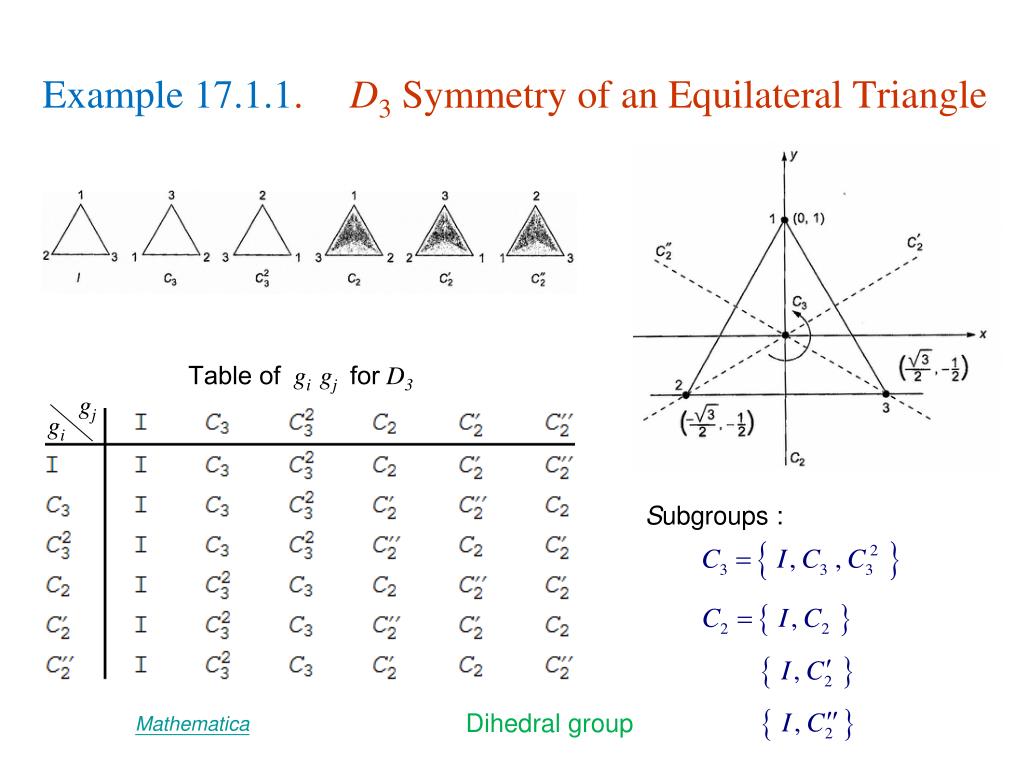
Equilateral Triangle Symmetry Group . The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. If you were to close your eyes, and a. •what are the possible symmetry rotations of an equilateral triangle? Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it.
from www.slideserve.com
The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. If you were to close your eyes, and a. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. •what are the possible symmetry rotations of an equilateral triangle? The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less.
PPT 17. Group Theory PowerPoint Presentation, free download ID5797607
Equilateral Triangle Symmetry Group The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. •what are the possible symmetry rotations of an equilateral triangle? The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. If you were to close your eyes, and a. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees.
From www.researchgate.net
Symmetry elements of an equilateral triangle in R 3 . Download Equilateral Triangle Symmetry Group Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. An equilateral triangle can. Equilateral Triangle Symmetry Group.
From mathmonks.com
Equilateral Triangle Definition, Properties, Formulas Equilateral Triangle Symmetry Group The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. •what are the possible symmetry rotations of an equilateral triangle? The symmetry group of an. Equilateral Triangle Symmetry Group.
From www.youtube.com
Group Theory Symmetry of Equilateral Triangle YouTube Equilateral Triangle Symmetry Group The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. If you were to. Equilateral Triangle Symmetry Group.
From www.teachoo.com
How many Lines of Symmetry of Equilateral Triangle? Teachoo Equilateral Triangle Symmetry Group If you were to close your eyes, and a. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. The symmetry group. Equilateral Triangle Symmetry Group.
From www.slideserve.com
PPT 17. Group Theory PowerPoint Presentation, free download ID5797607 Equilateral Triangle Symmetry Group An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. •what are the possible symmetry rotations of an equilateral triangle? The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. The symmetry group of an equilateral. Equilateral Triangle Symmetry Group.
From www.youtube.com
Symmetry Group Symmetry Group of an Equilateral Triangle (D3 Equilateral Triangle Symmetry Group Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. If you were to close your eyes, and a. The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add. Equilateral Triangle Symmetry Group.
From www.scribd.com
Symmetries of an Equilateral Triangle Group (Mathematics) Triangle Equilateral Triangle Symmetry Group An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. •what are the possible symmetry rotations of an equilateral triangle? The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. If you were to close your. Equilateral Triangle Symmetry Group.
From www.geogebra.org
Symmetries of an equilateral triangle GeoGebra Equilateral Triangle Symmetry Group If you were to close your eyes, and a. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. •what are the possible symmetry rotations of an equilateral triangle?. Equilateral Triangle Symmetry Group.
From demonstrations.wolfram.com
Symmetries of a Square and an Equilateral Triangle Wolfram Equilateral Triangle Symmetry Group The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements.. Equilateral Triangle Symmetry Group.
From www.youtube.com
Symmetry of an equilateral triangle YouTube Equilateral Triangle Symmetry Group The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. •what. Equilateral Triangle Symmetry Group.
From www.cuemath.com
How many lines of symmetry does an equilateral triangle have? [Solved] Equilateral Triangle Symmetry Group •what are the possible symmetry rotations of an equilateral triangle? The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. If you were to close your eyes, and a. Rotational symmetry •let 𝑅𝜃 be a counterclockwise. Equilateral Triangle Symmetry Group.
From www.youtube.com
11. Symmetry Group of the Equilateral Triangle YouTube Equilateral Triangle Symmetry Group Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. •what are the possible symmetry rotations of an equilateral triangle? If you were to close your. Equilateral Triangle Symmetry Group.
From imgbin.com
Equilateral Triangle Symmetry Group Action PNG, Clipart, Angle, Apex Equilateral Triangle Symmetry Group Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. If you were to close your eyes, and a. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. •what are the possible symmetry rotations of an equilateral triangle? An equilateral triangle can be rotated by 120 , 240 ,. Equilateral Triangle Symmetry Group.
From favpng.com
Equilateral Triangle Symmetry Group Action, PNG, 934x970px, Triangle Equilateral Triangle Symmetry Group Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. If you were to close your eyes, and a. •what are the possible symmetry rotations of an equilateral triangle? Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. The triangle group is the infinite symmetry group of a tiling. Equilateral Triangle Symmetry Group.
From mathmonks.com
Equilateral Triangle Definition, Properties, Formulas Equilateral Triangle Symmetry Group The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. If you were to close your eyes, and a. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. An equilateral triangle can be rotated. Equilateral Triangle Symmetry Group.
From www.shutterstock.com
Three Lines Symmetry Equilateral Triangle Stock Vector (Royalty Free Equilateral Triangle Symmetry Group •what are the possible symmetry rotations of an equilateral triangle? The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. If you were to close your eyes, and a. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group. Equilateral Triangle Symmetry Group.
From studylib.net
What are the symmetries of an equilateral triangle? In order to Equilateral Triangle Symmetry Group If you were to close your eyes, and a. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$. Equilateral Triangle Symmetry Group.
From www.slideserve.com
PPT Math 103 Contemporary Math PowerPoint Presentation, free download Equilateral Triangle Symmetry Group The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. If you were to close your eyes, and a. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. An equilateral triangle can be rotated by 120 , 240. Equilateral Triangle Symmetry Group.
From azveomwddo.blogspot.com
Equilateral Triangle Lines Of Symmetry, What Is A Line Of Symmetry Equilateral Triangle Symmetry Group The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. If you were to close your eyes, and a. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. An equilateral triangle can be rotated by 120 , 240. Equilateral Triangle Symmetry Group.
From www.teachoo.com
How many Lines of Symmetry of Equilateral Triangle? Teachoo Equilateral Triangle Symmetry Group If you were to close your eyes, and a. •what are the possible symmetry rotations of an equilateral triangle? The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group. Equilateral Triangle Symmetry Group.
From www.chegg.com
Question 1 The group of the equilateral triangle 180 Equilateral Triangle Symmetry Group If you were to close your eyes, and a. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. The triangle group is the infinite symmetry group of a tiling of the hyperbolic. Equilateral Triangle Symmetry Group.
From thirdspacelearning.com
What Is A Line Of Symmetry? Definition, Types, & Shapes Equilateral Triangle Symmetry Group Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. If you were to close your eyes, and a. An equilateral triangle can be rotated. Equilateral Triangle Symmetry Group.
From www.youtube.com
(Abstract Algebra 1) Symmetries of an Equilateral Triangle YouTube Equilateral Triangle Symmetry Group Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. •what are the possible symmetry rotations of an equilateral triangle? Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. An equilateral triangle can be. Equilateral Triangle Symmetry Group.
From www.youtube.com
Abstract Algebra Symmetries of an Equilateral Triangle YouTube Equilateral Triangle Symmetry Group If you were to close your eyes, and a. The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. •what are the possible symmetry rotations of an equilateral triangle? The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements.. Equilateral Triangle Symmetry Group.
From go.owu.edu
Group Stuff Equilateral Triangle Symmetry Group If you were to close your eyes, and a. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. •what are the possible symmetry rotations of an equilateral triangle? The triangle group is the infinite symmetry group of a tiling. Equilateral Triangle Symmetry Group.
From www.youtube.com
Symmetries of an Equilateral Triangle YouTube Equilateral Triangle Symmetry Group The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements.. Equilateral Triangle Symmetry Group.
From www.researchgate.net
Symmetric group of equilateral triangle Download Scientific Diagram Equilateral Triangle Symmetry Group An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. •what. Equilateral Triangle Symmetry Group.
From www.youtube.com
Dihedral Group Symmetries of an equilateral triangle Group Theory Equilateral Triangle Symmetry Group If you were to close your eyes, and a. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. •what are the possible symmetry rotations. Equilateral Triangle Symmetry Group.
From www.numerade.com
Determine the symmetry group and cornersymmetry group of an Equilateral Triangle Symmetry Group An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. If you were to close your eyes, and. Equilateral Triangle Symmetry Group.
From www.youtube.com
symmetries of equilateral triangle YouTube Equilateral Triangle Symmetry Group Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. If you were to close your eyes, and a. The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic. Equilateral Triangle Symmetry Group.
From flashman.neocities.org
Math 105 Notes 2906 Equilateral Triangle Symmetry Group •what are the possible symmetry rotations of an equilateral triangle? Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. If you were to close your eyes, and a. The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. The triangle group is the infinite symmetry. Equilateral Triangle Symmetry Group.
From www.youtube.com
Symmetric Group S3 Symmetry Group of an Equilateral Triangle Equilateral Triangle Symmetry Group The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of. Equilateral Triangle Symmetry Group.
From www.teachoo.com
Rotational Symmetry of Equailateral Triangle with Order [Teachoo] Equilateral Triangle Symmetry Group An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. Rotational symmetry •let 𝑅𝜃 be a counterclockwise rotation of 𝜃 degrees. The triangle group is the infinite symmetry group of a tiling of. Equilateral Triangle Symmetry Group.
From stock.adobe.com
three lines of symmetry of equilateral triangle Stock Vector Adobe Stock Equilateral Triangle Symmetry Group •what are the possible symmetry rotations of an equilateral triangle? The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less. Together the matrices $m$ and $r$ generate a group isomorphic to $s_3$, the symmetry group of the equilateral triangle. An equilateral triangle can be. Equilateral Triangle Symmetry Group.
From www.teachoo.com
State the number of lines of symmetry for (a) An equilateral triangle Equilateral Triangle Symmetry Group The symmetry group of an equilateral triangle is the dihedral group $d_3$ with $6$ elements. •what are the possible symmetry rotations of an equilateral triangle? If you were to close your eyes, and a. An equilateral triangle can be rotated by 120 , 240 , or 360 angles without really changing it. Together the matrices $m$ and $r$ generate a. Equilateral Triangle Symmetry Group.