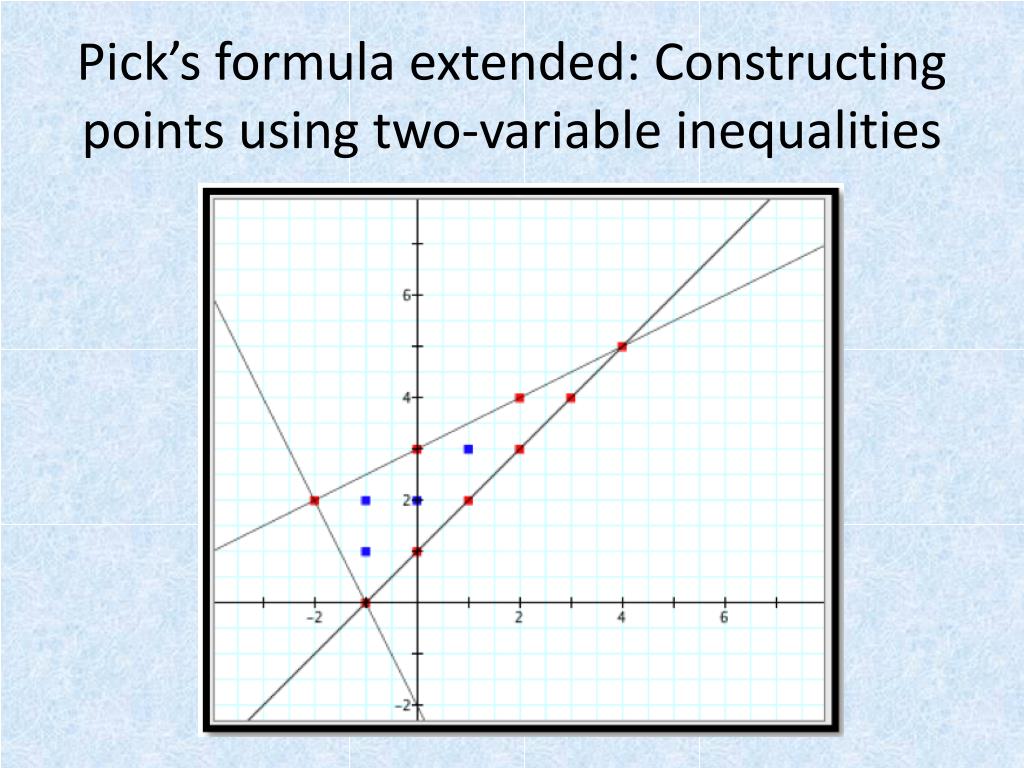
Pick's Formula . For example, in the figure above, the quadrilateral. A lattice polygon whose boundary consists of a sequence of. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Let b denote the number of lattice points on the polygon edges and i the number of. Let a be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Lattice points are points whose. The article shows how pick’s formula can be adapted to hold for these other shapes as well.
from www.slideserve.com
Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. For example, in the figure above, the quadrilateral. Let a be the area of a simply closed lattice polygon. A lattice polygon whose boundary consists of a sequence of. Let b denote the number of lattice points on the polygon edges and i the number of. The article shows how pick’s formula can be adapted to hold for these other shapes as well. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: Lattice points are points whose. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of.
PPT GEOMETRIC PROBABILITIES FROM FRACTIONS TO DEFINITE INTEGRALS USING TECHNOLOGY PowerPoint
Pick's Formula In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Let a be the area of a simply closed lattice polygon. A lattice polygon whose boundary consists of a sequence of. Let b denote the number of lattice points on the polygon edges and i the number of. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: Lattice points are points whose. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. The article shows how pick’s formula can be adapted to hold for these other shapes as well. For example, in the figure above, the quadrilateral.
From www.academia.edu
(PDF) A Colorful Proof of Pick’s Theorem Jack Graver Academia.edu Pick's Formula Lattice points are points whose. In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: Let b denote the number of lattice points. Pick's Formula.
From www.youtube.com
Proving Pick's Theorem Infinite Series YouTube Pick's Formula Lattice points are points whose. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Let a be the area of a simply closed lattice polygon. Pick’s theorem provides an elegant formula for the area of. Pick's Formula.
From theothermath.com
Discovering Pick’s Formula The Other Math Pick's Formula Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: For example, in the figure above, the quadrilateral. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. The article shows how pick’s formula can be adapted to. Pick's Formula.
From mundogenial.com
El teorema de Pick nos permite calcular de forma muy sencilla el área de un polígono que cumpla Pick's Formula Let b denote the number of lattice points on the polygon edges and i the number of. A lattice polygon whose boundary consists of a sequence of. For example, in the figure above, the quadrilateral. Lattice points are points whose. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in. Pick's Formula.
From www.youtube.com
Pick's Theorem YouTube Pick's Formula The article shows how pick’s formula can be adapted to hold for these other shapes as well. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem expresses the area of a polygon, all of whose vertices. Pick's Formula.
From www.slideserve.com
PPT Applications of Euler’s Formula for Graphs PowerPoint Presentation ID4088176 Pick's Formula Let a be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. The article shows how pick’s formula can be adapted to hold for these other shapes as well. In a triangulation of a polygon, where # vertices in primitive triangulation ,. Pick's Formula.
From www.chegg.com
Solved There is a formula, called Pick's Formula, for Pick's Formula Lattice points are points whose. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: The article shows how pick’s formula can be adapted to hold for these other shapes as well. For example, in the figure. Pick's Formula.
From studylib.net
Pick’s Theorem Examples Tom Davis Part I Pick's Formula Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. The article shows how pick’s formula can be adapted to hold for these other shapes as well. Pick's theorem gives a. Pick's Formula.
From www.researchgate.net
(PDF) Recurrent Theme of Pick's Theorem Pick's Formula Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Lattice points are points whose. A lattice polygon whose boundary consists of a sequence of. Let a be the area of a simply closed lattice polygon. Let b denote the number of. Pick's Formula.
From discover.hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Formula In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Let a be the area of a simply closed lattice polygon. Pick's theorem expresses the area of. Pick's Formula.
From www.geogebra.org
Pick's Theorem Explorer GeoGebra Pick's Formula For example, in the figure above, the quadrilateral. Let b denote the number of lattice points on the polygon edges and i the number of. The article shows how pick’s formula can be adapted to hold for these other shapes as well. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: A lattice polygon whose. Pick's Formula.
From www.slideserve.com
PPT Applications of Euler’s Formula for Graphs PowerPoint Presentation ID1805029 Pick's Formula In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Lattice points are points whose. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: The article shows how pick’s formula can be adapted to hold for these other shapes as well.. Pick's Formula.
From hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Formula In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. The article. Pick's Formula.
From www.slideserve.com
PPT GEOMETRIC PROBABILITIES FROM FRACTIONS TO DEFINITE INTEGRALS USING TECHNOLOGY PowerPoint Pick's Formula In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. The article shows how pick’s formula can be adapted to hold for these other shapes as well. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Pick's theorem gives a way to find the area of. Pick's Formula.
From yokehiang.blogspot.com
Yoke hiang & Math Pick's Formula The article shows how pick’s formula can be adapted to hold for these other shapes as well. In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Let a be the area of a simply closed lattice polygon. Pick's theorem expresses the area of a polygon,. Pick's Formula.
From en.etudes.ru
Pick’s formula / Etudes // Mathematical Etudes Pick's Formula A lattice polygon whose boundary consists of a sequence of. The article shows how pick’s formula can be adapted to hold for these other shapes as well. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Let b denote the number. Pick's Formula.
From www.geogebra.org
Fórmula de Pick GeoGebra Pick's Formula Let a be the area of a simply closed lattice polygon. A lattice polygon whose boundary consists of a sequence of. Let b denote the number of lattice points on the polygon edges and i the number of. The article shows how pick’s formula can be adapted to hold for these other shapes as well. Lattice points are points whose.. Pick's Formula.
From www.teachit.co.uk
Investigating area using Pick's theorem KS34 maths Teachit Pick's Formula A lattice polygon whose boundary consists of a sequence of. Let b denote the number of lattice points on the polygon edges and i the number of. Let a be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. For example, in. Pick's Formula.
From discover.hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Formula Let b denote the number of lattice points on the polygon edges and i the number of. For example, in the figure above, the quadrilateral. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Pick's theorem gives a way to find the area of. Pick's Formula.
From pt.slideshare.net
Teorema de pick Pick's Formula Lattice points are points whose. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: Let b denote the number of lattice points on the polygon edges and. Pick's Formula.
From maryluuna32.blogspot.com
"LA CAJITA DEL SABER" Fórmula de Pick y soluciones Pick's Formula In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Let a be the area of a simply closed lattice polygon. The article shows how pick’s formula can be adapted to hold for these other shapes as well. Let b denote the number of lattice points. Pick's Formula.
From www.youtube.com
Pick's Theorem YouTube Pick's Formula Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: Lattice points are points whose. Let a be the area of a simply closed lattice polygon. The article shows how pick’s formula can be adapted to hold for these other shapes as well. For example, in the figure above, the quadrilateral. Pick's theorem gives a way. Pick's Formula.
From www.geogebra.org
Lesson Pick's Theorem GeoGebra Pick's Formula Let b denote the number of lattice points on the polygon edges and i the number of. Let a be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. In a triangulation of a polygon, where # vertices in primitive triangulation ,. Pick's Formula.
From studylib.net
Pick`s Theorem Office for Mathematics, Science, and Technology Pick's Formula Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Lattice points are points whose. A lattice polygon whose boundary consists of a sequence of. In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation ,. Pick's Formula.
From colleenyoung.org
Pick’s Theorem Mathematics, Learning and Technology Pick's Formula Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. The article shows how pick’s formula can be adapted to hold for these other shapes as well. Let a be the area of a simply closed lattice polygon. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: In a triangulation of a polygon, where # vertices. Pick's Formula.
From nrich.maths.org
Pick's Theorem Poster Pick's Formula Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: For example, in the figure above, the quadrilateral. In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Lattice points are points whose. Let a be the area of a simply closed. Pick's Formula.
From www.slideserve.com
PPT Applications of Euler’s Formula for Graphs PowerPoint Presentation ID187298 Pick's Formula Let b denote the number of lattice points on the polygon edges and i the number of. For example, in the figure above, the quadrilateral. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. The article shows how pick’s formula can be adapted to hold for these other shapes as. Pick's Formula.
From www.youtube.com
Pick's Theorem to find the Area of Green Polygon instantly Important Geometry skills Pick's Formula Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. In a triangulation of a polygon, where # vertices in primitive triangulation , # edge segments in prmitive triangulation , and # primitive triangles. Let b denote the number of lattice points on the polygon edges and i the number of.. Pick's Formula.
From hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Formula A lattice polygon whose boundary consists of a sequence of. Are equilateral triangle lattices and hexagonal (like honeycomb) lattices. The article shows how pick’s formula can be adapted to hold for these other shapes as well. Let b denote the number of lattice points on the polygon edges and i the number of. For example, in the figure above, the. Pick's Formula.
From hr.mathigon.org
Pick’s Theorem Mathigon Pick's Formula Lattice points are points whose. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. A lattice polygon whose boundary consists of a sequence of. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Let. Pick's Formula.
From www.youtube.com
Pick's Theorem Area, boundary points, and interior points. YouTube Pick's Formula Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Let a be the area of a simply closed lattice polygon. Let b denote the number of lattice points on the polygon edges and i the number of. Are equilateral triangle lattices and hexagonal (like. Pick's Formula.
From www.slideserve.com
PPT Area PowerPoint Presentation, free download ID5396973 Pick's Formula Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. A lattice polygon whose boundary consists of a sequence of. Lattice points are points whose. Let. Pick's Formula.
From www.youtube.com
Pick's Theorem YouTube Pick's Formula The article shows how pick’s formula can be adapted to hold for these other shapes as well. Let a be the area of a simply closed lattice polygon. Let b denote the number of lattice points on the polygon edges and i the number of. A lattice polygon whose boundary consists of a sequence of. Lattice points are points whose.. Pick's Formula.
From www.youtube.com
Year 12 Maths A Use Pick's formula to find the area of shapes (part 1) YouTube Pick's Formula For example, in the figure above, the quadrilateral. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Lattice points are points whose. Pick’s theorem provides an elegant formula for the area of a simple lattice polygon: Let a be the area of a simply. Pick's Formula.
From connect.learnpad.com
Picks Theorem Content ClassConnect Pick's Formula Let b denote the number of lattice points on the polygon edges and i the number of. A lattice polygon whose boundary consists of a sequence of. The article shows how pick’s formula can be adapted to hold for these other shapes as well. For example, in the figure above, the quadrilateral. Pick's theorem gives a way to find the. Pick's Formula.