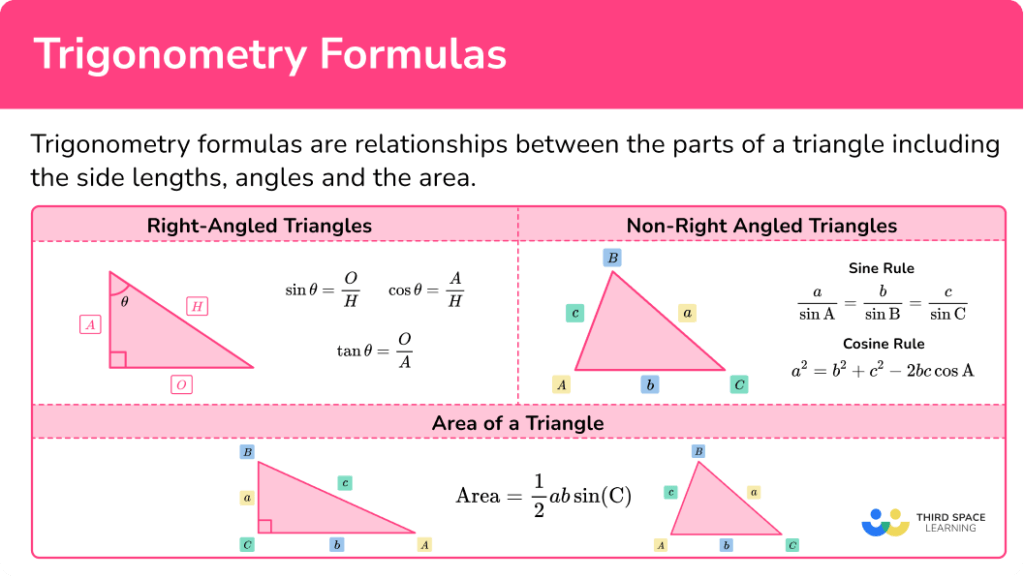
Triangle Area Formula Using Sine at Paul Jamison blog

Triangle Area Formula Using Sine. The area of a triangle is equal to half the product of two sides times the sine of the. Using the standard formula for the area of a triangle, we can derive. Area = a² × sin(β) × sin(γ) / (2 × sin(β + γ)) Use heron’s formula to determine the area of a triangle while only knowing the lengths of the sides. Area δ = ½ ab sin c. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the length of the perpendicular to the base from. Using the right triangle, we see that \(\sin(\theta) = \dfrac{h}{a}\). The most common formula for the area of a triangle would be:. Explain why this proves the formula for the area of a triangle. How to find the area of a triangle using sine when given two sides and an angle? The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle.

Area δ = ½ ab sin c. Explain why this proves the formula for the area of a triangle. Use heron’s formula to determine the area of a triangle while only knowing the lengths of the sides. Using the standard formula for the area of a triangle, we can derive. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the length of the perpendicular to the base from. Using the right triangle, we see that \(\sin(\theta) = \dfrac{h}{a}\). The area of a triangle is equal to half the product of two sides times the sine of the. How to find the area of a triangle using sine when given two sides and an angle? The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Area = a² × sin(β) × sin(γ) / (2 × sin(β + γ))

Trigonometry Formula GCSE Maths Steps & Examples

Triangle Area Formula Using Sine Using the standard formula for the area of a triangle, we can derive. Area δ = ½ ab sin c. Use heron’s formula to determine the area of a triangle while only knowing the lengths of the sides. How to find the area of a triangle using sine when given two sides and an angle? The area of a triangle is equal to half the product of two sides times the sine of the. Explain why this proves the formula for the area of a triangle. The most common formula for the area of a triangle would be:. Area = a² × sin(β) × sin(γ) / (2 × sin(β + γ)) Using the right triangle, we see that \(\sin(\theta) = \dfrac{h}{a}\). The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Using the standard formula for the area of a triangle, we can derive. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the length of the perpendicular to the base from.