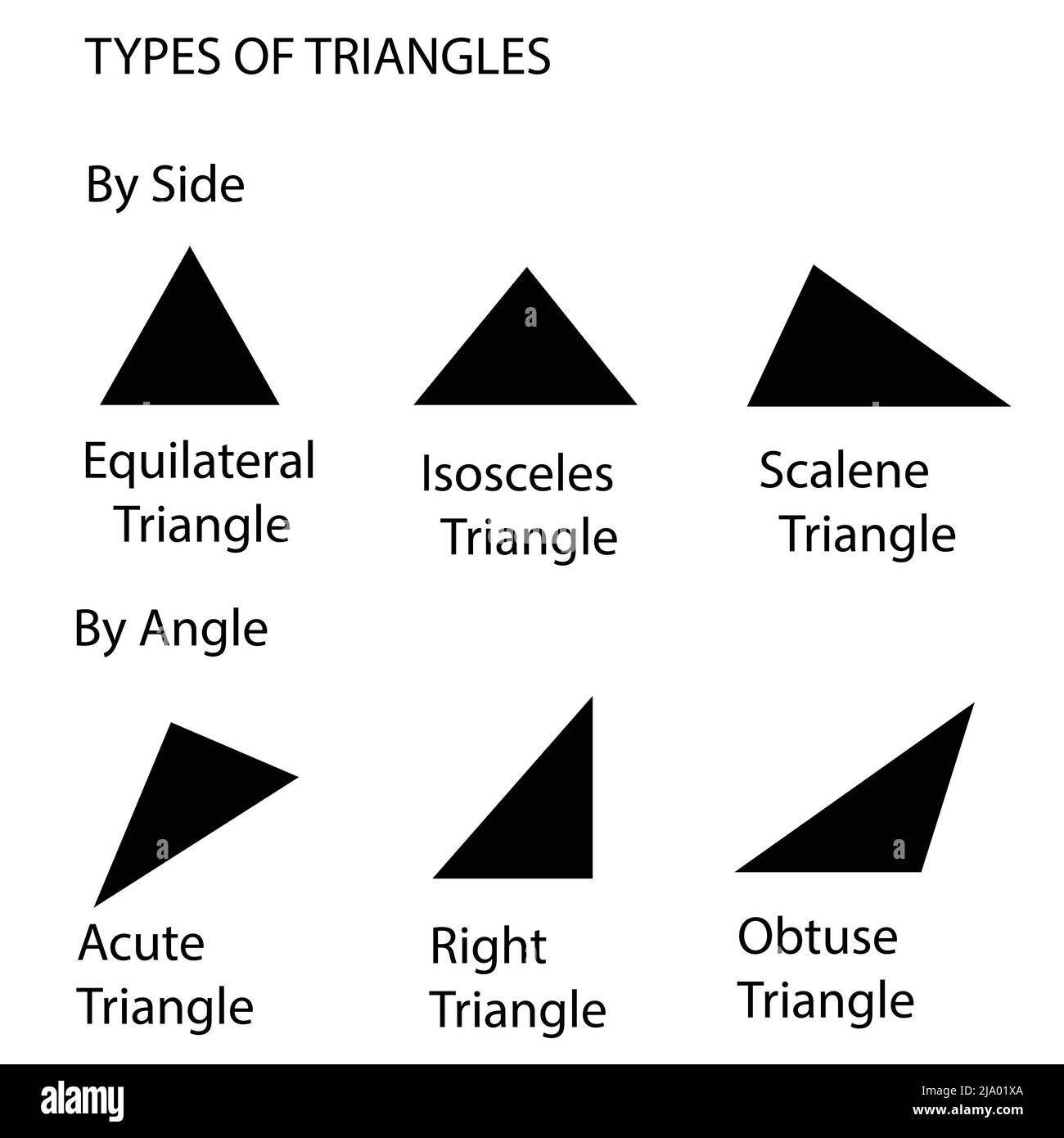
Are All Acute Triangles Similar at Gail Ingram blog

Are All Acute Triangles Similar. Take a closer look at these two types of triangles, their properties, and the formulas you'll use to work with them in math. There are a number of different ways to find out if two triangles are similar. The following are a few of the most common. Find the missing measurements in a pair of similar triangles. The corresponding angles are equal, and the corresponding sides are proportional. Identify equilateral, isosceles, scalene, acute, right, and obtuse triangles. Oblique triangles are broken into two types: An acute triangle is a triangle in which all the three interior angles are less than 90º. If two angles in one triangle are congruent to. A right triangle has a 90° angle, while an oblique triangle has no 90° angle. We can think of one similar triangle as an enlargement or a reduction of the other. In other words, the shape of the triangle is. Acute triangles and obtuse triangles. Two triangles are similar if they have the same shape but not necessarily the same size. An acute triangle is a type of triangle in which all the three internal angles of the triangle are acute.

There are a number of different ways to find out if two triangles are similar. Acute triangles and obtuse triangles. Although the three interior angles of the acute triangle lie within 0° to 90°, their sum is always 180 degrees. Identify corresponding sides of congruent and similar triangles. In other words, the shape of the triangle is. A right triangle has a 90° angle, while an oblique triangle has no 90° angle. The corresponding angles are equal, and the corresponding sides are proportional. Oblique triangles are broken into two types: If two angles in one triangle are congruent to. Identify equilateral, isosceles, scalene, acute, right, and obtuse triangles.

Different types of triangles vector illustration collection including

Are All Acute Triangles Similar Acute triangles and obtuse triangles. Take a closer look at these two types of triangles, their properties, and the formulas you'll use to work with them in math. Identify whether triangles are similar, congruent, or neither. Although the three interior angles of the acute triangle lie within 0° to 90°, their sum is always 180 degrees. We can think of one similar triangle as an enlargement or a reduction of the other. If two angles in one triangle are congruent to. There are a number of different ways to find out if two triangles are similar. The corresponding angles are equal, and the corresponding sides are proportional. An acute triangle is a type of triangle in which all the three internal angles of the triangle are acute. An acute triangle is a triangle in which all the three interior angles are less than 90º. Identify equilateral, isosceles, scalene, acute, right, and obtuse triangles. A right triangle has a 90° angle, while an oblique triangle has no 90° angle. In other words, the shape of the triangle is. Oblique triangles are broken into two types: Find the missing measurements in a pair of similar triangles. Identify corresponding sides of congruent and similar triangles.