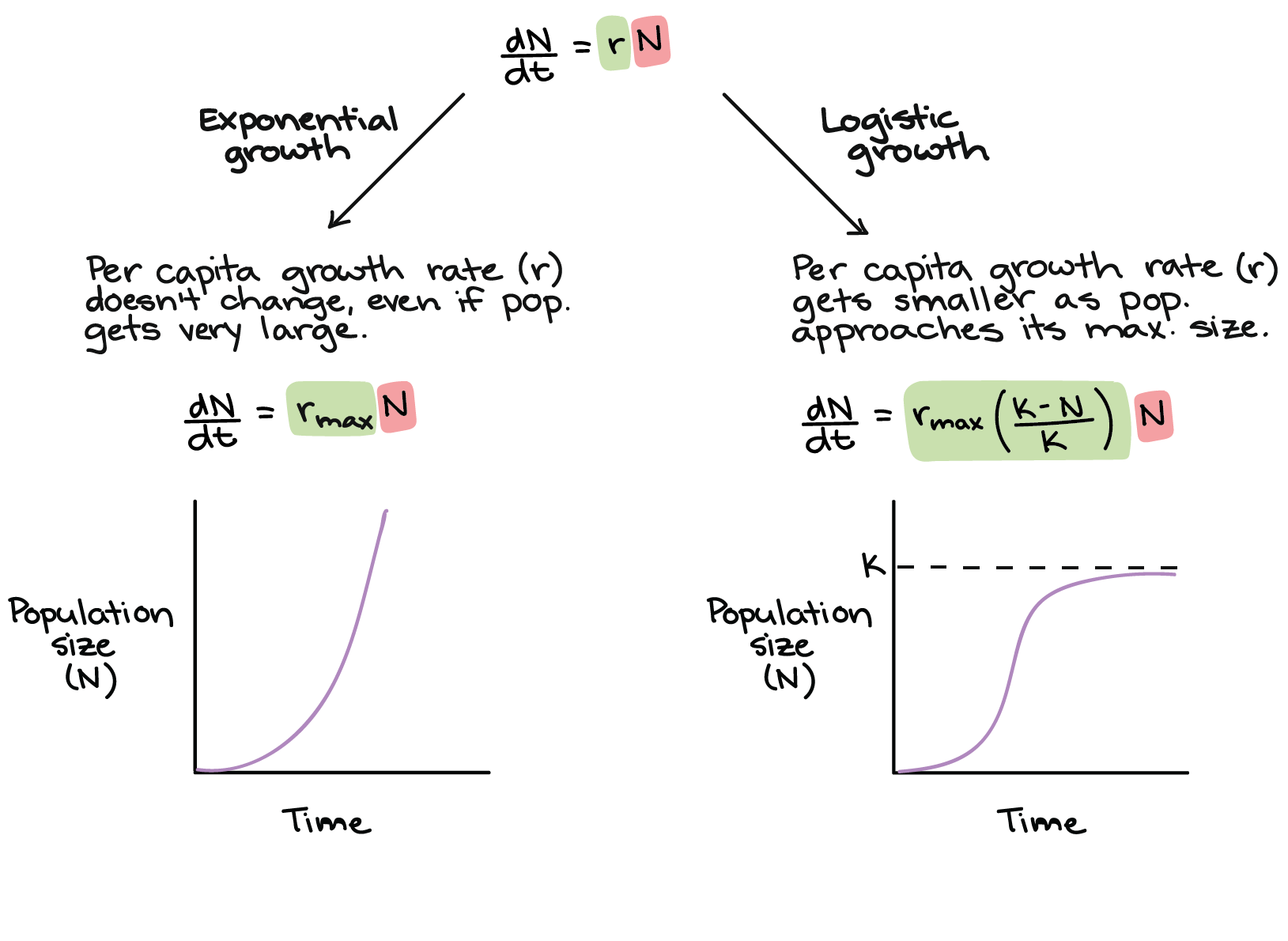
Differential Growth Model Definition . Two basic principles are involved, the idea of exponential growth and its ultimate control. What are the underlying principles of how populations change over time? Population growth models are mathematical representations that describe how populations change over time, based on factors such as. A differential equation is any equation of some unknown function that involves some derivative of the unknown function. Equation 6.27 involves derivatives and is called a differential equation. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. We learn more about differential equations in introduction to. How can we assess the accuracy of our models? Exponential growth and exponential decay are two of the most common applications of exponential functions. How can we use differential equations to realistically model the growth of a population? When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different.
from www.tessshebaylo.com
The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. How can we use differential equations to realistically model the growth of a population? A differential equation is any equation of some unknown function that involves some derivative of the unknown function. What are the underlying principles of how populations change over time? Exponential growth and exponential decay are two of the most common applications of exponential functions. Two basic principles are involved, the idea of exponential growth and its ultimate control. We learn more about differential equations in introduction to. When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. Equation 6.27 involves derivatives and is called a differential equation.
Exponential Growth Equations Tessshebaylo
Differential Growth Model Definition Two basic principles are involved, the idea of exponential growth and its ultimate control. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. How can we assess the accuracy of our models? When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. A differential equation is any equation of some unknown function that involves some derivative of the unknown function. We learn more about differential equations in introduction to. Two basic principles are involved, the idea of exponential growth and its ultimate control. Equation 6.27 involves derivatives and is called a differential equation. How can we use differential equations to realistically model the growth of a population? What are the underlying principles of how populations change over time? Exponential growth and exponential decay are two of the most common applications of exponential functions.
From www.flickr.com
differential growth diagram Jessica Rosenkrantz Flickr Differential Growth Model Definition Two basic principles are involved, the idea of exponential growth and its ultimate control. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. We learn more about differential equations in introduction to. How can we use differential equations to realistically model the growth of a. Differential Growth Model Definition.
From www.slideserve.com
PPT Differential Equations PowerPoint Presentation, free download Differential Growth Model Definition Population growth models are mathematical representations that describe how populations change over time, based on factors such as. Equation 6.27 involves derivatives and is called a differential equation. Exponential growth and exponential decay are two of the most common applications of exponential functions. How can we assess the accuracy of our models? A differential equation is any equation of some. Differential Growth Model Definition.
From www.researchgate.net
Schematic model representing the differential growth regulation of PR Differential Growth Model Definition Population growth models are mathematical representations that describe how populations change over time, based on factors such as. What are the underlying principles of how populations change over time? The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Exponential growth and exponential decay are two. Differential Growth Model Definition.
From www.researchgate.net
Differential growth, since 1977 Download Scientific Diagram Differential Growth Model Definition Exponential growth and exponential decay are two of the most common applications of exponential functions. We learn more about differential equations in introduction to. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the. Differential Growth Model Definition.
From www.geeksforgeeks.org
Logistic Population Growth Definition, Factors, Graph, Examples, FAQs Differential Growth Model Definition Exponential growth and exponential decay are two of the most common applications of exponential functions. Equation 6.27 involves derivatives and is called a differential equation. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. When studying population functions, different assumptions—such as exponential growth, logistic growth,. Differential Growth Model Definition.
From www.youtube.com
Logistic Growth Function and Differential Equations YouTube Differential Growth Model Definition Exponential growth and exponential decay are two of the most common applications of exponential functions. Equation 6.27 involves derivatives and is called a differential equation. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. What are the underlying principles of how populations change over time?. Differential Growth Model Definition.
From calcworkshop.com
Logistic Differential Equation Differential Growth Model Definition How can we assess the accuracy of our models? Two basic principles are involved, the idea of exponential growth and its ultimate control. Exponential growth and exponential decay are two of the most common applications of exponential functions. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. How can we use. Differential Growth Model Definition.
From www.slideserve.com
PPT Photoperiodic responses, light receptors and the biological clock Differential Growth Model Definition Population growth models are mathematical representations that describe how populations change over time, based on factors such as. Exponential growth and exponential decay are two of the most common applications of exponential functions. When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. The key model for growth (or decay when c < 0). Differential Growth Model Definition.
From www.pinterest.com
Differential Growth Research UVN Lab Conceptual model architecture Differential Growth Model Definition When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. Equation 6.27 involves derivatives and is called a differential equation. We learn more about differential equations in introduction to. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. How. Differential Growth Model Definition.
From www.slideshare.net
Blog ‘Differential growth’ this USED to be a successful Differential Growth Model Definition Exponential growth and exponential decay are two of the most common applications of exponential functions. Two basic principles are involved, the idea of exponential growth and its ultimate control. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold. Differential Growth Model Definition.
From n-e-r-v-o-u-s.com
poster differential growth 1 Nervous System Differential Growth Model Definition What are the underlying principles of how populations change over time? Population growth models are mathematical representations that describe how populations change over time, based on factors such as. Equation 6.27 involves derivatives and is called a differential equation. How can we assess the accuracy of our models? The key model for growth (or decay when c < 0) is. Differential Growth Model Definition.
From www.tessshebaylo.com
Exponential Growth Equations Tessshebaylo Differential Growth Model Definition How can we assess the accuracy of our models? When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. Exponential growth and exponential decay are two of the most common applications of exponential functions. Equation 6.27 involves derivatives and is called a differential equation. How can we use differential equations to realistically model the. Differential Growth Model Definition.
From www.researchgate.net
Differential growth, around three consecutive NBER troughs Download Differential Growth Model Definition Exponential growth and exponential decay are two of the most common applications of exponential functions. When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Equation 6.27 involves derivatives and. Differential Growth Model Definition.
From www.slideserve.com
PPT Corporate Finance Ross Westerfield Jaffe PowerPoint Presentation Differential Growth Model Definition Population growth models are mathematical representations that describe how populations change over time, based on factors such as. What are the underlying principles of how populations change over time? How can we use differential equations to realistically model the growth of a population? We learn more about differential equations in introduction to. Exponential growth and exponential decay are two of. Differential Growth Model Definition.
From www.researchgate.net
Differential growth, since 1977 Download Scientific Diagram Differential Growth Model Definition The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Exponential growth and exponential decay are two of the most common applications of exponential functions. A differential equation is any equation of some unknown function that involves some derivative of the unknown function. How can we. Differential Growth Model Definition.
From www.numerade.com
SOLVEDThe logistic differential equation models the growth rate of a Differential Growth Model Definition How can we use differential equations to realistically model the growth of a population? The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. We learn more about. Differential Growth Model Definition.
From www.slideserve.com
PPT DIFFERENTIAL EQUATIONS PowerPoint Presentation, free download Differential Growth Model Definition How can we use differential equations to realistically model the growth of a population? What are the underlying principles of how populations change over time? We learn more about differential equations in introduction to. Exponential growth and exponential decay are two of the most common applications of exponential functions. When studying population functions, different assumptions—such as exponential growth, logistic growth,. Differential Growth Model Definition.
From www.youtube.com
Calculus 12 Differential Growth Model Example 2 YouTube Differential Growth Model Definition Exponential growth and exponential decay are two of the most common applications of exponential functions. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. How can we use differential equations to realistically model the growth of a population? How can we assess the accuracy of our models? Two basic principles are. Differential Growth Model Definition.
From www.slideshare.net
Blog ‘Differential growth’ this USED to be a successful Differential Growth Model Definition The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Equation 6.27 involves derivatives and is called a differential equation. Exponential growth and exponential decay are two of the most common applications of exponential functions. Population growth models are mathematical representations that describe how populations change. Differential Growth Model Definition.
From www.researchgate.net
Differential growth rate of different components of human body weight Differential Growth Model Definition Population growth models are mathematical representations that describe how populations change over time, based on factors such as. Equation 6.27 involves derivatives and is called a differential equation. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. We learn more about differential equations in introduction. Differential Growth Model Definition.
From www.slideserve.com
PPT DIFFERENTIAL EQUATIONS PowerPoint Presentation, free download Differential Growth Model Definition Population growth models are mathematical representations that describe how populations change over time, based on factors such as. How can we use differential equations to realistically model the growth of a population? When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. What are the underlying principles of how populations change over time? We. Differential Growth Model Definition.
From www.youtube.com
Differential Equations Population Growth YouTube Differential Growth Model Definition What are the underlying principles of how populations change over time? We learn more about differential equations in introduction to. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Exponential growth and exponential decay are two of the most common applications of exponential functions. When. Differential Growth Model Definition.
From www.slideserve.com
PPT Corporate Finance Ross Westerfield Jaffe PowerPoint Presentation Differential Growth Model Definition Exponential growth and exponential decay are two of the most common applications of exponential functions. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. When studying population. Differential Growth Model Definition.
From www.youtube.com
Differential Equations Population Growth Proportionality Constant Differential Growth Model Definition Exponential growth and exponential decay are two of the most common applications of exponential functions. Two basic principles are involved, the idea of exponential growth and its ultimate control. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. A differential equation is any equation of some unknown function that involves some. Differential Growth Model Definition.
From www.semanticscholar.org
[PDF] Modeling Cancer Growth with Differential Equations Semantic Scholar Differential Growth Model Definition When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Exponential growth and exponential decay are two of the most common applications of exponential functions. How can we use differential. Differential Growth Model Definition.
From www.researchgate.net
Differential growth shapes. (a) Examples of folding geometries that Differential Growth Model Definition The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. Population growth models are mathematical representations that describe how populations change over time, based on factors such as. How can we assess the accuracy of our models? A differential equation is any equation of some unknown. Differential Growth Model Definition.
From www.researchgate.net
Differential Growth in the Harris Measure, 19102010. Notes The solid Differential Growth Model Definition Population growth models are mathematical representations that describe how populations change over time, based on factors such as. What are the underlying principles of how populations change over time? Two basic principles are involved, the idea of exponential growth and its ultimate control. A differential equation is any equation of some unknown function that involves some derivative of the unknown. Differential Growth Model Definition.
From www.slideserve.com
PPT Differential Equations PowerPoint Presentation, free download Differential Growth Model Definition What are the underlying principles of how populations change over time? Population growth models are mathematical representations that describe how populations change over time, based on factors such as. We learn more about differential equations in introduction to. When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. Two basic principles are involved, the. Differential Growth Model Definition.
From www.youtube.com
How to Solve Population Growth First Order Differential Equation Differential Growth Model Definition A differential equation is any equation of some unknown function that involves some derivative of the unknown function. We learn more about differential equations in introduction to. Exponential growth and exponential decay are two of the most common applications of exponential functions. Population growth models are mathematical representations that describe how populations change over time, based on factors such as.. Differential Growth Model Definition.
From www.cell.com
Differential growth dynamics control aerial organ geometry Current Biology Differential Growth Model Definition Two basic principles are involved, the idea of exponential growth and its ultimate control. Exponential growth and exponential decay are two of the most common applications of exponential functions. When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. How can we assess the accuracy of our models? We learn more about differential equations. Differential Growth Model Definition.
From www.ea-cr.eu
Differential Growth Differential Growth Model Definition Two basic principles are involved, the idea of exponential growth and its ultimate control. What are the underlying principles of how populations change over time? The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. We learn more about differential equations in introduction to. When studying. Differential Growth Model Definition.
From uvnlab.com
Differential Growth Research Yufan Xie Differential Growth Model Definition Equation 6.27 involves derivatives and is called a differential equation. Exponential growth and exponential decay are two of the most common applications of exponential functions. What are the underlying principles of how populations change over time? A differential equation is any equation of some unknown function that involves some derivative of the unknown function. Population growth models are mathematical representations. Differential Growth Model Definition.
From www.youtube.com
Application of Differential Equations Population Growth YouTube Differential Growth Model Definition When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. What are the underlying principles of how populations change over time? Equation 6.27 involves derivatives and is called a differential equation. How can we assess the accuracy of our models? A differential equation is any equation of some unknown function that involves some derivative. Differential Growth Model Definition.
From www.onenewspage.com
Exponential growth, differential equations, One News Page VIDEO Differential Growth Model Definition When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different. We learn more about differential equations in introduction to. What are the underlying principles of how populations change over time? Equation 6.27 involves derivatives and is called a differential equation. Exponential growth and exponential decay are two of the most common applications of exponential. Differential Growth Model Definition.
From www.youtube.com
Development EconomicsIChapter 3Growth Models and Theories of Differential Growth Model Definition How can we use differential equations to realistically model the growth of a population? Equation 6.27 involves derivatives and is called a differential equation. Exponential growth and exponential decay are two of the most common applications of exponential functions. How can we assess the accuracy of our models? When studying population functions, different assumptions—such as exponential growth, logistic growth, or. Differential Growth Model Definition.